《电路》课程教学资源（PPT课件）第十三章 非正弦周期电流电路和信号的频谱

电路非正弦周期电流电路和信号的频谱例4交直流共存电路E返上回贝

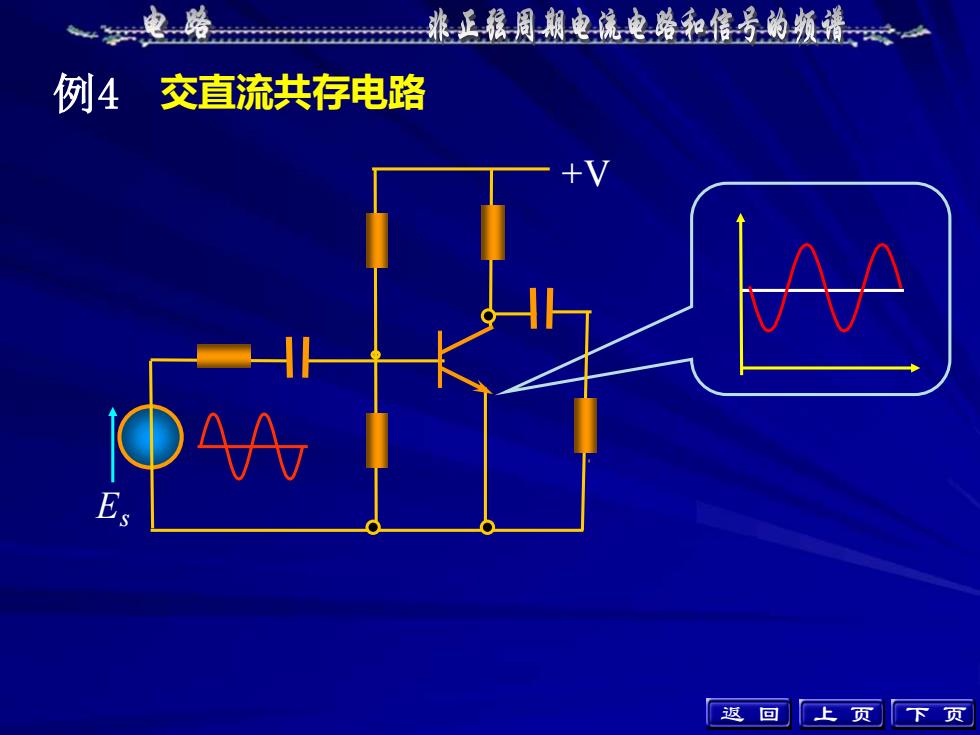
例4 交直流共存电路 +V Es 返 回 上 页 下 页

州电路非正弦周期电流电路和信号的频谱13.2周期函数分解为傅里叶级数若周期函数满足狄利赫利条件：①周期函数极值点的数目为有限个；②间断点的数目为有限个；③在一个周期内绝对可积，即：[f(t)] dt <00可展开成收敛的傅里叶级数注意一般电工里遇到的周期函数都能满足狄利赫利条件返上回页下页

13.2 周期函数分解为傅里叶级数  f t t   T ( ) d 0 若周期函数满足狄利赫利条件： ①周期函数极值点的数目为有限个； ②间断点的数目为有限个； ③在一个周期内绝对可积，即： 可展开成收敛的傅里叶级数 注意 一般电工里遇到的周期函数都能满足 狄利赫利条件。 返 回 上 页 下 页

#州电路非正弦周期电流电路和信号的频谱山周期函数展开成傅里叶级数：直流分量基波（和原f(t)= A. + Am cos(@t +d)+函数同频）二次谐波+ Am cos(2ot +Φ,)+.:（2倍频）+ A.cos(not +Φ) +高次谐波nm8+Z Am cos(kot +Φk)f(t) = A +k=1返上回页?页

直流分量 基波（和原 函数同频） 二次谐波 （2倍频） 高次谐波 ( ) cos( ) 1 0  1  = = + + k km k f t A A kt  f (t) = A0 + A1m cos(1 t +1 ) + + A2m cos(21 t +2 ) + + A nm cos(n1 t +n ) + 周期函数展开成傅里叶级数： 返 回 上 页 下 页

电路非正弦周期电流电路和信号的频谱山也可表示成：cos(ko, t +Φ)=a, cosko, t + b, sin ko tAKnZ[a, cosko t +b, sin kot]f(t)=a. +k=-1系数之间的关系为：A. = αoAm= Va +bha, = Akm cospb,=-Am sin Φ-bd= arctanq返上回页下页

( ) [ cos sin ] 1 1 0 1 f t a a k t b k t k k  k    = = + + A k t a k t b k t km 1 + k = k 1 + k 1 cos(   ) cos  sin  也可表示成： k k k k km k k km k km k k a b a A b A A a b A a − = = = − = + = arctan cos sin 2 2 0 0    系数之间的关系为： 返 回 上 页 下 页

#电路非正弦周期电流电路和信号的频谱山系数的计算：A4 =α=()d 2元f(t)cos(kot)d(o it)JO元12元f(t)sin(kot)d(, t)元求出Ao、ak、bk便可得到原函数f(t)的展开式。返上回页K页

   = = = = 2π 0 1 1 2π 0 1 1 0 0 0 ( )sin( )d( ) π 1 ( )cos( )d( ) π 1 ( )d 1 b f t k t t a f t k t t f t t T A a k k T     求出A0、ak、bk便可得到原函数 f(t) 的展开式。 系数的计算： 返 回 上 页 下 页