
第三节 均匀流动的沿程水头损失和基本方程式 一、均匀流动方程式 均匀流只能发生在长直的管道或渠道这一类断面形状和大小都沿程不变的流动中,因此 只有沿程损失,而无局部损失。为了导出沿程阻力系数的计算公式,首先建立沿程损失和沿 程阻力之间的关系。在图5-5所示的均匀流中,在任何的两个断面11和2-2列能量方程 图5-5圆管均匀流动 乙++-Z+++h 2g 2g 由均匀流的性质: 4-,5 2828 代入上式,得 ,=2+Z)-(2+Z) (5-9) 考虑所取流段在流向上的受力平衡条件。设两断面间的距离为L,过流断面面积 A=A=A,在流向上,该流段所受的作用力有: 重力分量 YAlcosa 端面压力 PA P2A 管壁压力 t112m% 其中一一管壁切应力:0一一圆管半径。 在均匀流中,流体质点作等速运动,加速度为零,因此,以上各力的合力为零,考虑到 各力的作用方向,得 6
6 第三节 均匀流动的沿程水头损失和基本方程式 一、均匀流动方程式 均匀流只能发生在长直的管道或渠道这一类断面形状和大小都沿程不变的流动中,因此 只有沿程损失,而无局部损失。为了导出沿程阻力系数的计算公式,首先建立沿程损失和沿 程阻力之间的关系。在图 5-5 所示的均匀流中,在任何的两个断面 1-1 和 2-2 列能量方程 图 5-5 圆管均匀流动 1 2 2 2 2 2 2 2 1 1 1 1 2 2 + + = + + + hl − g p Z g p Z 由均匀流的性质: hl hf g g = = 2 2 2 2 2 2 11 代入上式,得 ( ) ( ) 2 2 1 1 Z p Z p hf = + − + (5-9) 考虑所取流段在 流向上的 受力平衡条 件。设两断 面间的距离为 L ,过流断面 面积 A1=A2=A,在流向上,该流段所受的作用力有: 重力分量 Al cos 端面压力 p1A p2A 管壁压力 1 2 0 l r 其中τ0——管壁切应力;r0——圆管半径。 在均匀流中,流体质点作等速运动,加速度为零,因此,以上各力的合力为零,考虑到 各力的作用方向,得
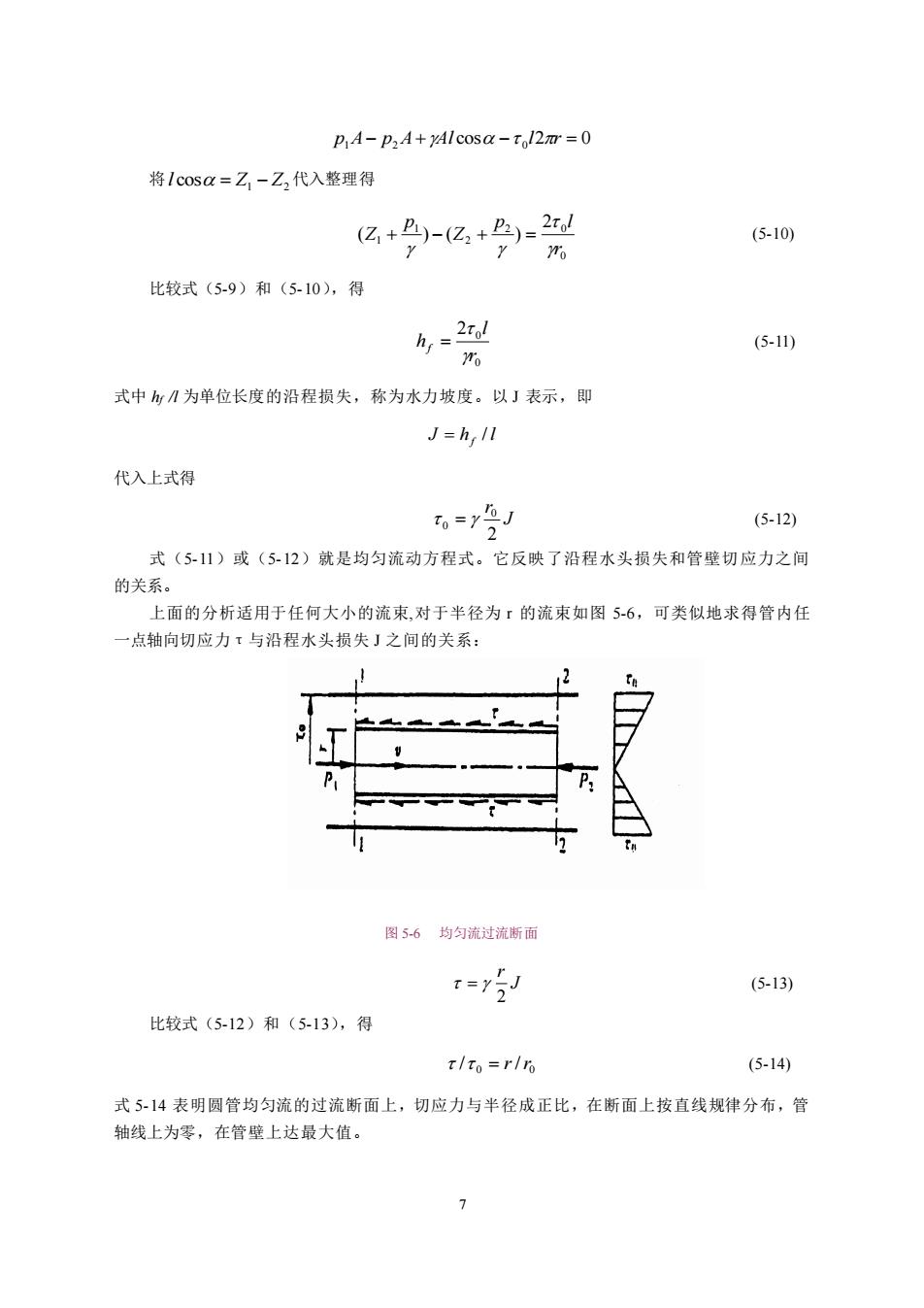
p A-p2A+yAlcosa-tol2=0 将1cosa=Z-Z,代入整理得 (亿+B)-(亿,+色)-2 (5-10) 比较式(5-9)和(5-10),得 421 (5-1) 式中:为单位长度的沿程损失,称为水力坡度。以J表示,即 J=h,Il 代入上式得 fy (5-12) 式(5-11)或(5-12)就是均匀流动方程式。它反映了沿程水头损失和管壁切应力之间 的关系。 上面的分析适用于任何大小的流束,对于半径为r的流束如图5-6,可类似地求得管内任 点轴向切应力与沿程水头损失」之间的关系: 图56均匀流过流新面 =y5 (5-13) 比较式(5-12)和(5-13),得 T/To=r/r (5-14) 式5-14表明圆管均匀流的过流断面上,切应力与半径成正比,在断面上按直线规律分布,管 轴线上为零,在管壁上达最大值
7 p1A− p2A+Al cos − 0 l2r = 0 将 1 2 l cos = Z − Z 代入整理得 0 2 0 2 1 1 2 ( ) ( ) r p l Z p Z + − + = (5-10) 比较式(5-9)和(5-10),得 0 0 2 r l hf = (5-11) 式中 hf /l 为单位长度的沿程损失,称为水力坡度。以 J 表示,即 J h l f = / 代入上式得 J r 2 0 0 = (5-12) 式(5-11)或(5-12)就是均匀流动方程式。它反映了沿程水头损失和管壁切应力之间 的关系。 上面的分析适用于任何大小的流束,对于半径为 r 的流束如图 5-6,可类似地求得管内任 一点轴向切应力τ与沿程水头损失 J 之间的关系: 图 5-6 均匀流过流断面 J r 2 = (5-13) 比较式(5-12)和(5-13),得 0 0 / = r/r (5-14) 式 5-14 表明圆管均匀流的过流断面上,切应力与半径成正比,在断面上按直线规律分布,管 轴线上为零,在管壁上达最大值

二、沿程阻力系数的计算 均匀流基本方程式给出了沿程水头损失与切应力ī的关系,而τ的大小与流体的流动形 态有关。圆管中的层流运动,可以看成无数无限薄的圆筒层,一个套着一个地相对滑动,各 流层间互不掺混。可以证明这种轴对称的流动各流层间的切应力大小满足牛顿内摩擦定律式 即 r-出 (5-15) 由于速度“随r的增大而减小,所以等式右边加负号,以保证t为正。 取立均匀流动方程式(5-13)和式(515),整理得 在均匀流中,J值不随r而变。积分上式,并代入边界条件:r=n时,u=0,得 (5-16 可见,断面流速分布是以管中心线为轴的旋转抛物面,见图5-7。 w 图57圆管中层流的速度分布 0时,即在管轴上,达最大流速: (5-17) 将式(5-16)代入平均流速定义式 v-0 ∫dju-2md 得平均流速为 (6-18) 比较式(5-17)和(5-18),得
8 二、沿程阻力系数的计算 均匀流基本方程式给出了沿程水头损失与切应力τ的关系,而τ的大小与流体的流动形 态有关。圆管中的层流运动,可以看成无数无限薄的圆筒层,一个套着一个地相对滑动,各 流层间互不掺混。可以证明这种轴对称的流动各流层间的切应力大小满足牛顿内摩擦定律式 即 dr du = − (5-15) 由于速度 u 随 r 的增大而减小,所以等式右边加负号,以保证τ为正。 取立均匀流动方程式(5-13)和式(5-15),整理得 rdr J du 2 = − 在均匀流中,J 值不随 r 而变。积分上式,并代入边界条件:r=r0 时,u=0,得 ( ) 4 2 2 0 r r J u = − (5-16) 可见,断面流速分布是以管中心线为轴的旋转抛物面,见图 5-7。 图 5-7 圆管中层流的速度分布 r=0 时,即在管轴上,达最大流速: 2 2 max 0 4 16 d J r J u u = = (5-17) 将式(5-16)代入平均流速定义式 A u rdr A udA A Q r A = = = 0 0 2 得平均流速为 2 2 0 8 32 d J r J = = (5-18) 比较式(5-17)和(5-18),得

(5-19) 即平均流速等于最大流速的一半。 根据式(5-18),得 =J1=32l (5-20) 此式从理论上证明了层流沿程损失和平均流速一次方成正比。这个结论和雷诺实验的结果 致。上式称为哈根一泊肃叶公式(定律),这种层流运动称(哈根)泊肃叶流动。 将式(5-20)写成计算沿程损失的一般形式,则 ,=”32W-64.1.心 d2g yd2 Re d 2g 由此式,可得圆管层流的沿程阻力系数的计算式: (5-21) 它表明圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙无关。 【例5-3】设石油在圆管中作恒定有压均匀流动。已知管径d=10cm,流量Q-500cms, 石油密度p=850kg/m3,运动粘度v=1.8×10m/s。试求管轴处最大流速4,半径=2cm 处的流速,管壁处切应力t,以及每米管长的沿程损失:。 【解】首先判断流态。断面平均流速V为 u-号0-67m/-037a Re-_00637x01=354<20为层流 y1.8×10- 4mx=2D-2×0.0637-0.127m/s %=0-0127x0-01067m: 2 层流 1=64、64 Re34=0.18 -Pr2=018×850x00637=0073Pa 9
9 max 2 1 = (5-19) 即平均流速等于最大流速的一半。 根据式(5-18),得 2 32 d l h J l f = = (5-20) 此式从理论上证明了层流沿程损失和平均流速一次方成正比。这个结论和雷诺实验的结果一 致。上式称为哈根—泊肃叶公式(定律),这种层流运动称(哈根)泊肃叶流动。 将式(5-20)写成计算沿程损失的一般形式,则 d g l d l d g l hf Re 2 32 64 2 2 2 2 = = = 由此式,可得圆管层流的沿程阻力系数的计算式: Re 64 = (5-21) 它表明圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙无关。 【例 5-3】 设石油在圆管中作恒定有压均匀流动。已知管径 d=10cm,流量 Q=500cm3 /s, 石油密度ρ=850 kg/m3,运动粘度 1.8 10 m /s −5 2 = 。试求管轴处最大流速 umax ,半径 r=2cm 处的流速 2 u ,管壁处切应力 0 以及每米管长的沿程损失 hf 。 【解】 首先判断流态。断面平均流速 为 cm s m s A Q 6.37 / 0.0637 / 10 4 500 2 = = = = 354 2000 1.8 10 0.0637 0.1 Re 5 = = = − d 为层流 u 2 2 0.0637 0.127m/s max = = = m s r r u u ) 0.1067 / 5 2 (1 ) 0.127 (1 2 2 2 0 2 2 = max − = − = 层流, 0.18 354 64 Re 64 = = = 850 0.0637 0.078Pa 8 0.18 8 2 2 0 = = =
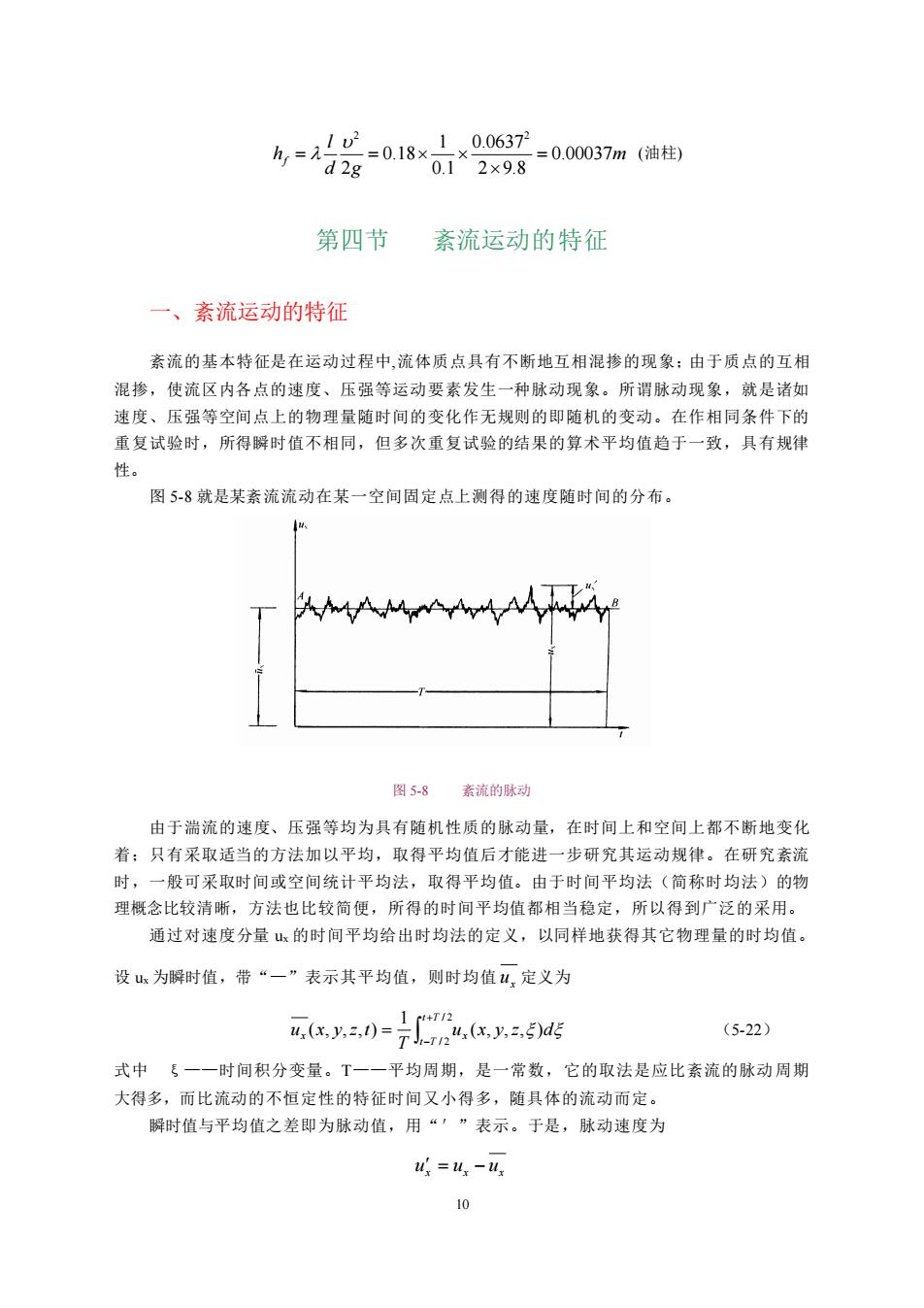
女=号5-a1s*92g=0omn陶 第四节 紊流运动的特征 一、紊流运动的特征 紊流的基本特征是在运动过程中,流体质点具有不断地互相混掺的现象:由于质点的互相 混掺,使流区内各点的速度、压强等运动要素发生一种脉动现象。所谓脉动现象,就是诸如 速度、压强等空间点上的物理量随时间的变化作无规则的即随机的变动。在作相同条件下的 重复试验时,所得瞬时值不相同,但多次重复试验的结果的算术平均值趋于一致,具有规伸 性 图5-8就是某紊流流动在某一空间固定点上测得的速度随时间的分布 图5-8素流的脉动 由于湍流的速度、压强等均为具有随机性质的脉动量,在时间上和空间上都不断地变化 着:只有采取适当的方法加以平均,取得平均值后才能进一步研究其运动规律。在研究奈流 时,一般可采取时间或空间统计平均法,取得平均值。由于时间平均法(简称时均法)的物 理概念比较清晰,方法也比较简便,所得的时间平均值都相当稳定,所以得到广泛的采用。 通过对速度分量u的时间平均给出时均法的定义,以同样地获得其它物理量的时均值 设为瞬时值,带“一”表示其平均值,则时均值山,定义为 .-u(.y.ds (5-22) 式中。一一时间积分变量。T一一平均周期,是一常数,它的取法是应比紊流的脉动周期 大得多,而比流动的不恒定性的特征时间又小得多,随具体的流动而定。 解时值与平均值之差即为脉动值,用“'”表示。于是,脉动速度为 =w-4
10 m d g l hf 0.00037 2 9.8 0.0637 0.1 1 0.18 2 2 2 = = = (油柱) 第四节 紊流运动的特征 一、紊流运动的特征 紊流的基本特征是在运动过程中,流体质点具有不断地互相混掺的现象;由于质点的互相 混掺,使流区内各点的速度、压强等运动要素发生一种脉动现象。所谓脉动现象,就是诸如 速度、压强等空间点上的物理量随时间的变化作无规则的即随机的变动。在作相同条件下的 重复试验时,所得瞬时值不相同,但多次重复试验的结果的算术平均值趋于一致,具有规律 性。 图 5-8 就是某紊流流动在某一空间固定点上测得的速度随时间的分布。 图 5-8 紊流的脉动 由于湍流的速度、压强等均为具有随机性质的脉动量,在时间上和空间上都不断地变化 着;只有采取适当的方法加以平均,取得平均值后才能进一步研究其运动规律。在研究紊流 时,一般可采取时间或空间统计平均法,取得平均值。由于时间平均法(简称时均法)的物 理概念比较清晰,方法也比较简便,所得的时间平均值都相当稳定,所以得到广泛的采用。 通过对速度分量 ux 的时间平均给出时均法的定义,以同样地获得其它物理量的时均值。 设 ux 为瞬时值,带“—”表示其平均值,则时均值 x u 定义为 + − = / 2 / 2 ( , , , ) 1 ( , , , ) t T t T x ux x y z d T u x y z t (5-22) 式中 ξ——时间积分变量。T——平均周期,是一常数,它的取法是应比紊流的脉动周期 大得多,而比流动的不恒定性的特征时间又小得多,随具体的流动而定。 瞬时值与平均值之差即为脉动值,用“′”表示。于是,脉动速度为 ux = ux −ux