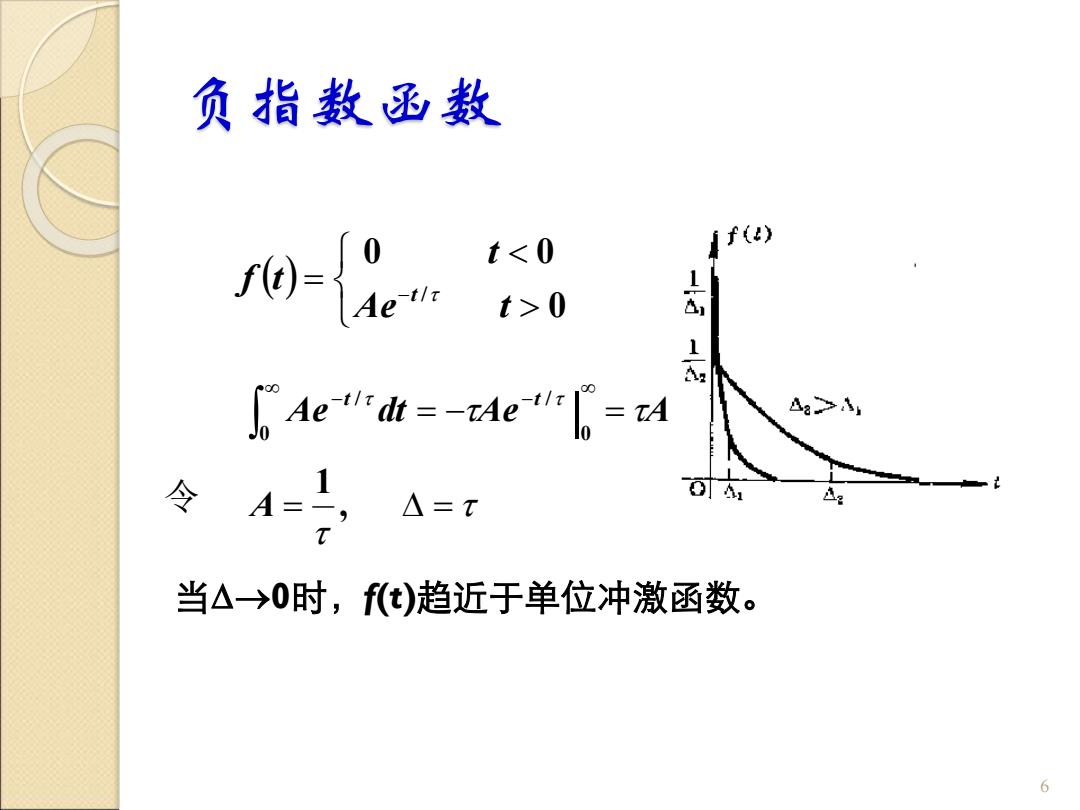
负指数函数 r0=0 t<0 f() 0 & de "dt=-Meprd 4a> 令 A 1 △=t 04 d 当△→0时,f(t)趋近于单位冲激函数
负指数函数 当→0时,f(t)趋近于单位冲激函数。 6 ( ) = − 0 0 0 / Ae t t f t t = = = − = − − , 1 | 0 / 0 / A Ae dt Ae A t t 令

§-2冲激函数的性质 ·冲激函数是阶跃函数的导数 1.6-8 t>0 根据定义 t<0 'd(5)5=et) 故得 de(t)=s(t) dt 7
§-2 冲激函数的性质 ❖ 冲激函数是阶跃函数的导数 7 ( ) ( ) ( ) ( ) (t) dt d t d t t t d t t = = = − − 0 0 1 0 根据定义 故得

冲激函数的性质 筛分性:除了在原点外,对所有t,t)=0,因此,除 了t=0外,对所有t,乘积f)(t)也将为零。在t=0, ft)=fO),故得 ()()=f(0)5(t) si))()=(0) f)少5(t-6)t=f) lf5t),(t-o)》 f()(t一) f(to) f1 o 8
冲激函数的性质 ❖ 筛分性:除了在原点外,对所有t,(t)=0,因此,除 了t=0外,对所有t,乘积f(t)(t)也将为零。在t=0, f(t)=f(0),故得 8 f (t) (t) = f (0) (t) f (t) (t)dt = f (0) (t)dt = f (0) (t)dt = f (0) − − ( ) ( ) ( ) 0 0 f t t − t dt = f t −

§3电容电压和电感电流的跃变 若电容的电流只能为有限值,则电容电压不能跃变; 若电感的电压只能为有限值,则电感电流不能跃变。 在实际电路中,由于电路满足KCL和KVL,电容电压 和电感电流发生跃变都是可能出现的,在这种情况下, 电容电流和电感电压都应为无限大。 必 当电容电压和电感电流发生跃时,讨论电容电压和电 感电流初始值的计算问题,就需要运用冲激电流和冲 激电压的概念
§-3电容电压和电感电流的跃变 ❖ 若电容的电流只能为有限值,则电容电压不能跃变; 若电感的电压只能为有限值,则电感电流不能跃变。 ❖ 在实际电路中,由于电路满足KCL和KVL,电容电压 和电感电流发生跃变都是可能出现的,在这种情况下, 电容电流和电感电压都应为无限大。 ❖ 当电容电压和电感电流发生跃时,讨论电容电压和电 感电流初始值的计算问题,就需要运用冲激电流和冲 激电压的概念。 9

冲激电流概念 由电容的VAR可表为 a,)=u6)+名∫店 设t0=0,仁0+ ue(0.)-ue()+id 若Q6t)流经电容 40,)=0)+号 10
冲激电流概念 由电容的VAR 可表为 10 ( ) ( ) = + t t C C i d C u t u t 0 1 0 ( ) ( ) ( ) ( ) C Q u u i d C u u C C C C = + = + + − + − + − 0 0 1 0 0 0 0 设t0=0-,t=0+ 若Q(t)流经电容