
(Ⅲ)r检验法 2(x-0y-可 记 r= 2x利20,列 当r>r,时,拒绝Ho;否则就接受Ho 其中r.V1+(n-2)/.(1n-2)
(Ⅲ)r 检验法 当|r|> r 1− 时,拒绝 H0;否则就接受 H0. 记 = = = − − − − = n i n i i i n i i i x x y y x x y y r 1 1 2 2 1 ( ) ( ) ( )( ) 其中 ( ) ( ) 1 1 1 1 2 1, 2 r n F n − − = + − −

2.回归系数的置信区间 阝。和阝,置信水平为1-a的置信区间分别为 和 B-1en-2)6.1L,A+1en-26.1 o2的置信水平为1-0的置信区间为 0. 4a2xm列
2.回归系数的置信区间 0 和 1 置信水平为 1-α的置信区间分别为 − − + + − + − − xx e xx e L x n t n L x n t n 2 2 1 0 2 2 1 0 1 ( 2) ˆ ˆ , 1 ( 2) ˆ ˆ 和 − − + − − − e xx n e Lxx t n L t ( 2) ˆ / ˆ ( 2) ˆ / , ˆ 2 1 1 2 1 1 2 的置信水平为 1- 的置信区间为 − − − ( 2) , ( 2) 2 2 2 2 1 n Q n Qe e

3.预测与控制 (1)预测 用%的回归值。=B。+Bx作为%的预测值 y的置信水平为1-,的预测区间为 [-6(x),+6(xo)] -引 L 特别,当n很大且xo在x附近取值时, y的置信水平为1-o的预测区间近似为
3.预测与控制 (1)预测 用 y0的回归值 0 0 1 0 ˆ ˆ y ˆ = + x 作为 y0的预测值. 0 y 的置信水平为1− 的预测区间为 ˆ ( ), ˆ ( ) 0 0 0 0 y − x y + x 其中 ( ) xx e L x x n x t n 2 0 2 1 0 1 ( ) ˆ ( 2) 1 − = − + + − 特别,当 n 很大且 x0在 x 附近取值时, y 的置信水平为1− 的预测区间近似为 − + − − 2 1 2 1 ˆ ˆ , ˆ ˆ u y u y e e

(2)控制 要求:y=B。+Bx+g的值以1-a的概率落在指定区间y',y") 只要控制x满足以下两个不等式 -6(x)≥y',+6(x)≤y" 要求y”-y'≥26(x).若)-6(x)=y',)-6(x)=y”分别有解x' 和x",即)-6(x)=y',)+δ(x")=y” 则(x',x"就是所求的x的控制区间, 返回
(2)控制 要求: y = + x + 0 1 的值以1− 的概率落在指定区间(y , y ) 只要控制 x 满足以下两个不等式 y ˆ − (x) y , y ˆ + (x) y 要求 y − y 2 (x).若 y ˆ − (x) = y , y ˆ − (x) = y 分别有解 x 和 x ,即 y ˆ − (x ) = y , y ˆ + (x ) = y . 则(x , x )就是所求的 x 的控制区间. 返回
四、可线性化的一元非线性回归 (曲线回归) 例2出钢时所用的盛钢水的钢包,由于钢水对耐火材料的侵蚀, 容积不断增大我们希望知道使用次数与增大的容积之间的关 系对一钢包作试验, 测得的数据列于下表: 使用次数 增大容积 使用次数 增大容积 2 6.42 10 10.49 3 8.20 11 10.59 4 9.58 12 10.60 5 9.50 13 10.80 6 9.70 14 10.60 1 10.00 15 10.90 8 9.93 6 10.76 9 9.99 解答
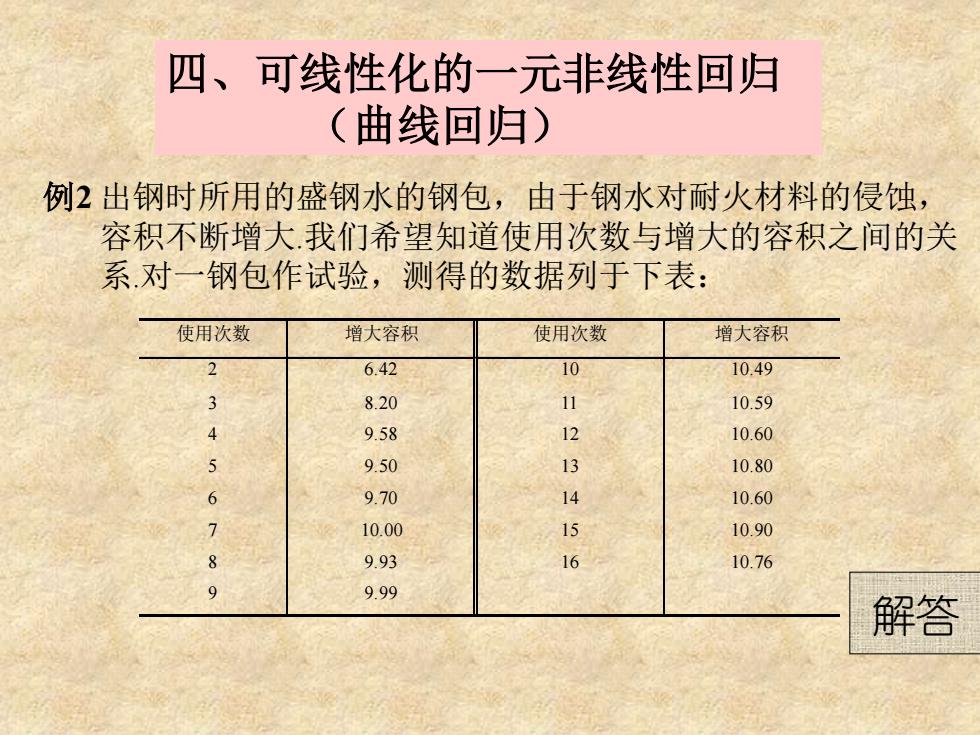
四、可线性化的一元非线性回归 (曲线回归) 例2 出钢时所用的盛钢水的钢包,由于钢水对耐火材料的侵蚀, 容积不断增大.我们希望知道使用次数与增大的容积之间的关 系.对一钢包作试验,测得的数据列于下表: 使用次数 增大容积 使用次数 增大容积 2 3 4 5 6 7 8 9 6.42 8.20 9.58 9.50 9.70 10.00 9.93 9.99 10 11 12 13 14 15 16 10.49 10.59 10.60 10.80 10.60 10.90 10.76 解答