11 15059 8.5 散点图 6.5 6 10 12 14 16 此即非线性回归或曲线回归问题(需要配曲线) 配曲线的一般方法是: 先对两个变量x和y作n次试验观察得(x,y,),i=1,2,n画出散点图, 根据散点图确定须配曲线的类型.然后由对试验数据确定每一类曲线的未知 参数α和b.采用的方法是通过变量代换把非线性回归化成线性回归,即采用 非线性回归线性化的方法
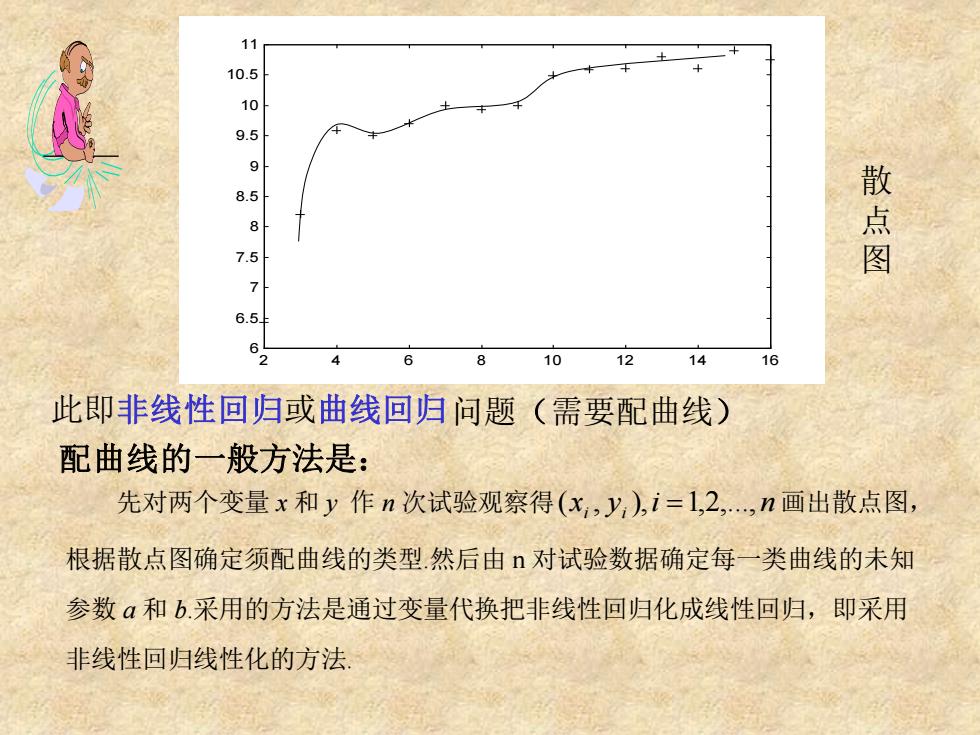
2 4 6 8 10 12 14 16 6 6.5 7 7.5 8 8.5 9 9.5 10 10.5 11 散 点 图 此即非线性回归或曲线回归问题(需要配曲线) 配曲线的一般方法是: 先对两个变量 x 和 y 作 n 次试验观察得 (xi , yi ),i =1,2,., n 画出散点图, 根据散点图确定须配曲线的类型.然后由 n 对试验数据确定每一类曲线的未知 参数 a 和 b.采用的方法是通过变量代换把非线性回归化成线性回归,即采用 非线性回归线性化的方法

通常选择的六类曲线如下: (1)双曲线1=a+b y (2)幂函数曲线y=ax,其中x>0,a>0 (3)指数曲线y=aer其中参数a>0 (4)倒指数曲线y=ae1x其中a>0, (5)对数曲线y=a+blogx,x>0 6)S型曲线y= a+be-x 解例2.由散点图我们选配到指数曲线y=ae1x 根据线性化方法,算得6=-1.1107,A=2.4587 返回 由此 a=e=11.6789 1.1107 最后得 y=11.6789ex
通常选择的六类曲线如下: (1)双曲线 x b a y = + 1 (2)幂函数曲线 y=a b x , 其中 x>0,a>0 (3)指数曲线 y=a e bx 其中参数 a>0. (4)倒指数曲线 y=a / e b x 其中 a>0, (5)对数曲线 y=a+blog x,x>0 (6)S 型曲线 1 e x y a b − = + 返回 解例 2.由散点图我们选配到指数曲线 y=a / e b x 根据线性化方法,算得 2.4587 ˆ 1.1107, ˆ b = − A = 由此 ˆ ˆ e 11.6789 A a = = 最后得 1.1107 11.6789e x y − =

数学模型及定义 一般称 Y=XB+8 E(8)=0,COV(8,8)=o2I 为高斯-马尔可夫线性模型(k元线性回归模型),并简记为(Y,XB,σ21)】 y 「1x12 BT 81 Y= ,X= 17X21 X22 X2k B- B 8= 62 yn 1 xm Xn2 LB」 En y=P+Bx1++Bxk称为回归平面方程. 返回 线性模型(Y,XB,o21n)考虑的主要问题是: (1)用试验值(样本值)对未知参数B和σ作点估计和假设检验,从而建立y与 X1,X2,.,Xk之间的数量关系 (2)在x=xo1,x32=x2,x=xok,处对y的值作预测与控制,即对y作区间估计
一、数学模型及定义 一般称 2 ( ) 0,COV( , ) n Y X E I = + = = 为高斯-马尔可夫线性模型(k 元线性回归模型),并简记为( , , ) 2 n Y X I 1 2 n y y Y y = , 11 12 1 21 22 2 1 2 1 . 1 . 1 . k k n n nk x x x x x x X x x x = , 0 1 k = , 1 2 n = k k y = + x +.+ x 0 1 1 称为回归平面方程. 返回 线性模型 ( , , ) 2 n Y X I 考虑的主要问题是: (1)用试验值(样本值)对未知参数 和 2 作点估计和假设检验,从而建立 y 与 k x , x ,.,x 1 2 之间的数量关系; (2)在 , ,., , 1 01 2 02 k 0k x = x x = x x = x 处对 y 的值作预测与控制,即对 y 作区间估计