
3、最大似然估计 。 欲使得效用模型可以估计,就必须为随机误差项 选择一种特定的概率分布。 ·两种最常用的分布是标准正态分布和逻辑 (logistic)分布,于是形成了两种最常用的二元 选择模型一Probit模型和Logit模型。 ·最大似然函数及其估计过程如下:
3、最大似然估计 • 欲使得效用模型可以估计,就必须为随机误差项 选择一种特定的概率分布。 • 两种最常用的分布是标准正态分布和逻辑 (logistic)分布,于是形成了两种最常用的二元 选择模型—Probit模型和Logit模型。 • 最大似然函数及其估计过程如下:

标准正态分布或逻 F(-t)=1-F(t) 辑分布的对称性 P(y,=1)=P(y,>O)=P(4>-X:B) =1-P(4≤-X:B) =1-F(-X:B)=F(X;B) P(v.2.)=(1-F(X;B)F(X;B) 片=0 y=1 似然函数 L=(F(X;B))2(1-F(X;B)) i=1
F(−t) = 1− F(t) P y P y P P F F i i i i ( ) ( ) ( ) ( ) ( ) ( ) * * * = = = − = − − = − − = 1 0 1 1 X X X X i i i i P y y yn F F y y i i ( , , , ) ( ( )) ( ) 1 2 0 1 = 1− = = Xi Xi L F F i n = − − = ( (X )) ( (X )) i y i i 1 1 yi 1 标准正态分布或逻 辑分布的对称性 似然函数
In L= ∑O,InF(X,B)+(1-y,)In(1-F(X,B》 i=1 In L -fi 1阶极值条件 X=0 OB ·在样本数据的支持下,如果知道概率分布函数 和概率密度函数,求解该方程组,可以得到模 型参数估计量
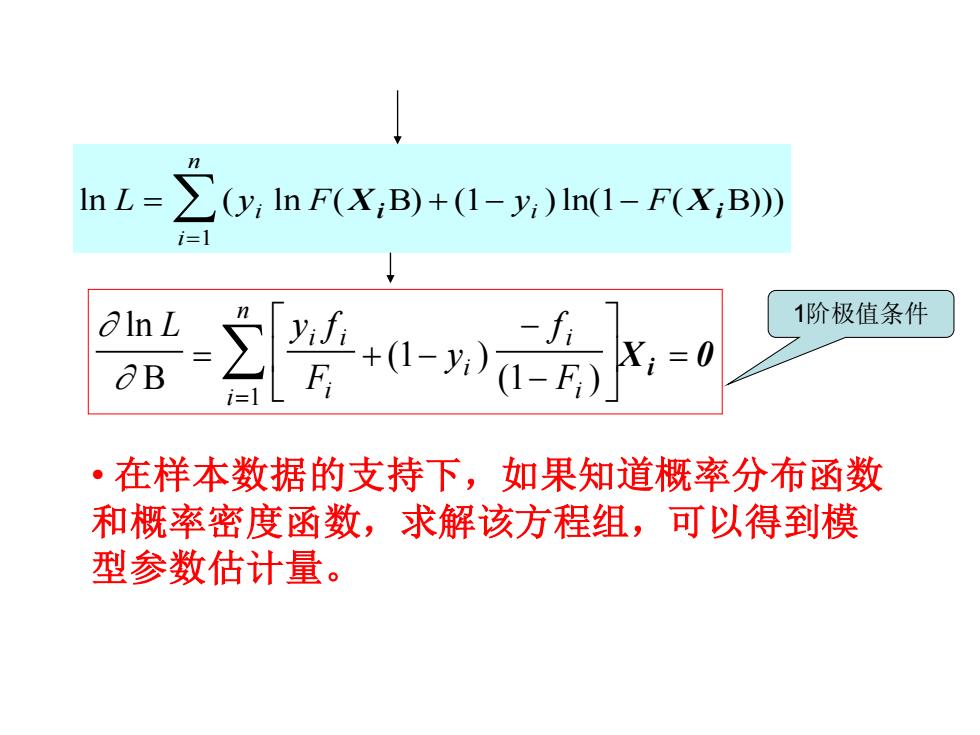
ln L ( y ln F( ) ( y ) ln( F( ))) i i i n = + − − = Xi 1 1 Xi 1 ln ( ) ( ) L y f F y f F i i i i i i i n = + − − − = = 1 1 1 X 0 i • 在样本数据的支持下,如果知道概率分布函数 和概率密度函数,求解该方程组,可以得到模 型参数估计量。 1阶极值条件

三、二元Probit离散选择模型及其参数 估计
三、二元Probit离散选择模型及其参数 估计

1、标准正态分布的概率分布函数 F0)=∫(2x)cxp-x22)d -0 f(x)=(2π)片exp(-x2/2)
1、标准正态分布的概率分布函数 F t x dx t ( ) = ( ) exp(− ) − − 2 2 1 2 2 f (x) = ( ) exp(− x ) − 2 2 1 2 2