
中国科学技术大学物理学院叶邦角整理 29届全国中学生物理竞赛决赛试题 一、(15分) 如图,竖直的光滑墙面上有A和B两个钉子,二者处于同一水平高度,间距为1,有一原长为1、劲度 系数为k的轻橡皮筋,一端由A钉固定,另一端系有一质量为广札的小 Ag 球,其中g为重力加速度.钉子和小球都可视为质点,小球和任何物体碰 撞都是完全非弹性碰撞而且不发生粘连.现将小球水平向右拉伸到与A钉 距离为21的C点,B钉恰好处于橡皮筋下面并始终与之光滑接触.初始时 刻小球获得大小为。=圆 方向竖直向下的速度,试确定此后小球沿 竖直方向的速度为零的时刻 参考解答: 以B钉为坐标原点建坐标系Oy,如图1所示.小 球在被释放后受到本身重力和橡皮筋的弹力两个 力的作用.设小球相对于原点O(即B钉)的位置 由位矢r表示,则弹力可表示为 F=-kr (1) 小球的运动方程在Oy坐标系下分解为 ma,=-kx (2) may =-ky-mg (3) 定义y方向新坐标y=y+mg/k,(3)式可改写为 ma,=-k' (4) 图1 由(2)和(4)式知小球在水平和竖直方向都做简谐振动.其振动方程可表示为 x(1)=A cos(or+) (5) y'()-Acos(t+9,) (6) 利用参考圆可得到小球速度的表达式 v(t)=-A,@sin(at+o) () v,(t)=-A,@sin(at+) (8) 将如下初始条件 x(0)=1 (9) 0=竖号 (10) v.(0)=0 (a1) ”0)=- 2 (12) 代入(5)至(8)式,可解得振幅A,和A及位相P,和g,·再利用w=Vk/m=2√gi,上 述振动方程和速度表达式可用已知量表示为: (13) (14) -2@m2昌 (15) 中国科学技术大学物理学院叶邦角整理
29 届全国中学生物理竞赛决赛试题 一、(15 分) 如图,竖直的光滑墙面上有 A 和 B 两个钉子,二者处于同一水平高度,间距为l ,有一原长为l 、劲度 系数为 k 的轻橡皮筋,一端由 A 钉固定,另一端系有一质量为 m= g kl 4 的小 球,其中 g 为重力加速度.钉子和小球都可视为质点,小球和任何物体碰 撞都是完全非弹性碰撞而且不发生粘连.现将小球水平向右拉伸到与 A 钉 距离为 2l 的 C 点,B 钉恰好处于橡皮筋下面并始终与之光滑接触.初始时 刻小球获得大小为 2 0 gl v 、方向竖直向下的速度,试确定此后小球沿 竖直方向的速度为零的时刻. 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 ,厚2+到 (16) 由(16)式可求出小球速度沿y方向分量第一次为零的时刻,即),()=0,其中 0= 3n D 8 Vg (17) 此后,如果小球沿y方向的振动没有中断,当小球沿y方向的振动到达最大振幅处时,(16) 式右端便等于零.然而,按(16)式右端等于零所求出的其它时刻并不是满足题意的解:因 为在按(16)式求出的竖直速度等于零的第二个时刻之前,小球将和B钉发生碰撞,碰撞 时刻为 31 t。= 4Vg (18) 此时,按(13)和(14)两式可知 ))-0 (19) (20) 这恰好是B钉的位置.这样,小球将在t=t。时和B钉发生完全非弹性碰撞,碰撞后小 球速度为零:由于碰撞过程时间极短,t。时刻就是小球速度沿y方向分量第二次为零的时刻。 碰撞后小球并不和B钉粘连,所以小球将沿y方向做一维的简谐振动,由(4)式可知此振 动周期为 (21) 0 每经过半个振动周期T,都会出现速度为零的情况(此时自然有?,=0)·这样,除(17) 和(18)式确定的前两个特定时刻之外,每当 a4+=m+马5, T +22 ,n=1,2,… (22) 时,小球速度都为零,因而其沿y方向的速度分量也为零, 评分标准:本题15分 (2)式1分,(3)或(4)式1分: (5)(6)(7)(8)(13)(14)(15)(16)(17)(18)(21)式各1分, (22)式2分 二、(20分) 如图所示,三个质量均为m的小球固定于由刚性轻质杆构成的丁字形架的三个顶点A、B和C处.AD ⊥BC,且AD=BD=CD=,小球可视为质点,整个杆球体系置于水平桌面上,三个小球和桌面接触,轻质杆架 悬空.桌面和三小球之间的静摩擦和滑动摩擦因数均为μ,在AD杆上距A点a/4 和3a/4两处分别施加一垂直于此杆的推力,且两推力大小相等、方向相反. B 1.试论证在上述推力作用下,杆球体系处于由静止转变为运动的临界状态时, 推力 三球所受桌面的摩擦力都达到最大静摩擦力: 2.如果在AD杆上有一转轴,随推力由零逐渐增加,整个装置将从静止开始绕 A 该转轴转动.问转轴在AD杆上什么位置时,推动该体系所需的推力最小,并求出 该推力的大小, 推力 中国科学技术大学物理学院叶邦角整理
二、(20 分) 如图所示,三个质量均为 m 的小球固定于由刚性轻质杆构成的丁字形架的三个顶点 A、B 和 C 处.AD ⊥BC,且 AD=BD=CD=a,小球可视为质点,整个杆球体系置于水平桌面上,三个小球和桌面接触,轻质杆架 悬空.桌面和三小球之间的静摩擦和滑动摩擦因数均为μ,在 AD 杆上距 A 点 a/4 和 3a/4 两处分别施加一垂直于此杆的推力,且两推力大小相等、方向相反. 1.试论证在上述推力作用下,杆球体系处于由静止转变为运动的临界状态时, 三球所受桌面的摩擦力都达到最大静摩擦力; 2.如果在 AD 杆上有一转轴,随推力由零逐渐增加,整个装置将从静止开始绕 该转轴转动.问转轴在 AD 杆上什么位置时,推动该体系所需的推力最小,并求出 该推力的大小. 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 参考解答: 1.将固连于杆的A、B和C三端的小球分别称为A、B和C球.由于杆的质量可忽略, 则三小球所受桌面支持力的大小都等于其重力.这一结论可通过如下方法证明:以B球为 例,将B球连同一小段杆隔离出来作为研究对象,分析其在竖直方向的受力情况,它受小球 重力和桌面支持力,这两个力的作用线过小球和桌面接触点并垂直于桌面,如果这两个力大 小不相等,则在该研究对象的杆截面处必存在非零的竖直方向力,才能满足在竖直方向力的 平衡方程.然而,如果存在这样的力,则相对于小球球心,该研究对象的力矩不为零,这违 反研究对象的力矩平衡条件,因此,桌面支持力必等于小球重力,根据如上分析,三小球所 受最大静摩擦力的大小都为 fr=umg (1) 体系由静止向运动转变的临界状态可能存在两种不同的情况,第一种情况是两个小球所 受摩擦力的大小已达到∫x,而第三个小球尚未达到∫x·这种临界状态对应着体系将绕第 三个小球转动,第二种情况为三小球所受摩擦力的大小都已达到∫∝,这种临界状态意味 着体系将发生平移或绕三小球以外的某点转动,也可以是平动和转动的合成运动,总之,这 是一种对应着三小球都将开始运动的临界状态 可以论证所谓的第一种临界状态是不合理的.换言之,这种临界状态是不可能发生的. 为证明这种观点,可设B和C球所受摩擦力己达到∫x,而A球摩擦力尚未达到该值,在 此基础上如果再稍增加推力,一种可能是B和C球仍保持静止,但是A球的摩擦力值随之 增加直到fx,但这就转变成第二种临界状态了,另一种情况是A球摩擦力虽未达到∫m: 但也不再增加,而B和C球已开始运动,此时A球必为体系的转动中心,B和C球处于绕 之转动的临界状态,由于在该临界状态系统仍静止,所以在水平桌面内其所受外力的矢量和 为零,用矢量形式表示为 fa+fe+fc=0 上式左边的三个力分别为A、B和C球所受的静摩擦力.B和C球的摩擦力大小为 后=:=寸x,其方向垂直于两小球到A球的连线.将(1)式正交分解,可求得A球所受 的摩擦力大小为 f=v2f>fm (2) 该值已超过最大静摩擦力∫mx,这意味着A球不可能处于静止状态,所以这种临界状态不可 能出现.同理可知,体系分别绕B或C球开始转动的临界状态也不可能出现,因为这样的 状态对应的B或C球的摩擦力为 fuc =12+2fom>fo (3) 可见该值也超过了最大静摩擦力、终上所述,在体系由静到动的临界状态三小球所受摩擦力 中国科学技术大学物理学院叶邦角整理
中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 都达到最大摩擦力fx· B 2.用G表示转轴在AD杆上的位置,用F表示推力的大小,在体系绕转轴刚好开始转 动的临界状态,桌面对A、B和C三球的最大静摩擦力(大小均为4mg)的方向分别和连 线GA,GB和GC垂直,如图所示.并且它们对G点的总力矩刚好和外力矩相平衡.设G点 与D点的距离为xa,则力矩平衡方程为 umg(2x'a +a+a-xa)=Fa (4) 此式可进一步整理为 -小+4-(=0 (5) 这个方程有实根的条件是 (6 上式简化为 F≥2(N5+1)4mg (7) 这意味着只有F满足如上条件时,才能在AD杆上找到一个转轴位置而使体系运动起来.换 言之, F=2(N3+1)mg (8) 是推动该体系转动的最小推力,将上式代入(5)式,可求出 3 (9) 评分标准:本题20分, 第1问8分, (1)式2分,(2)(3)式各3分 第2问12分, (4)式4分,(6)式2分,(7)(8)(9)式各2分.用其它方法正确得到(8)式的,给(6) (7)(8)式的分值. 中国科学技术大学物理学院叶邦角整理
中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理
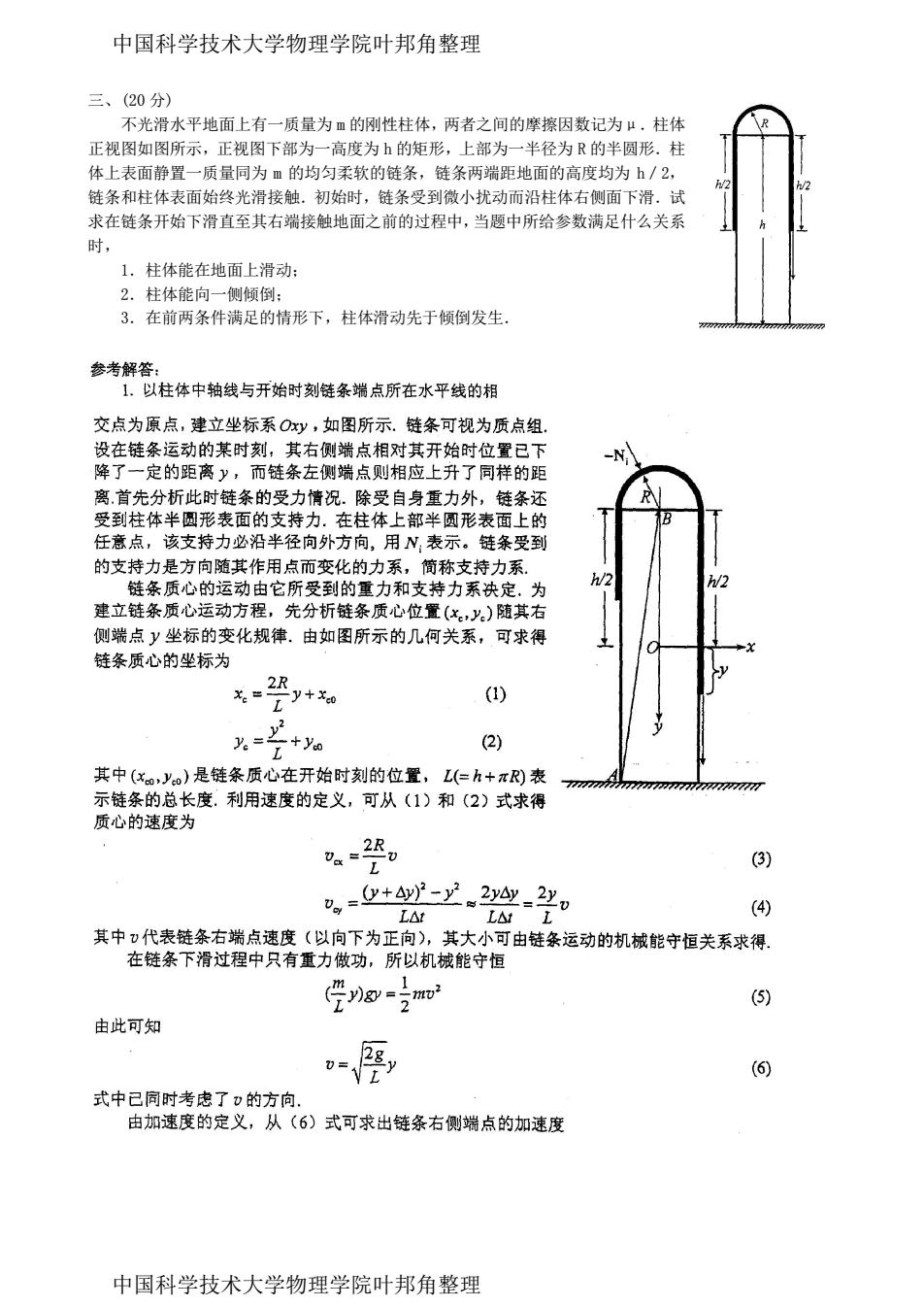
中国科学技术大学物理学院叶邦角整理 三、(20分) 不光滑水平地面上有一质量为m的刚性柱体,两者之间的摩擦因数记为μ,柱体 正视图如图所示,正视图下部为一高度为的矩形,上部为一半径为R的半圆形.柱 体上表面静置一质量同为m的均匀柔软的链条,链条两端距地面的高度均为h/2, 链条和柱体表面始终光滑接触.初始时,链条受到微小扰动而沿柱体右侧面下滑.试 求在链条开始下滑直至其右端接触地面之前的过程中,当题中所给参数满足什么关系 时, 1.柱体能在地面上滑动: 2.柱体能向一侧倾倒 3.在前两条件满足的情形下,柱体滑动先于倾倒发生. 参考解答: 1.以柱体中轴线与开始时刻链条端点所在水平线的相 交点为原点,建立坐标系Oxy,如图所示.链条可视为质点组. 设在链条运动的某时刻,其右侧端点相对其开始时位置已下 -N 降了一定的距离y,而链条左侧端点则相应上升了同样的距 离首先分析此时链条的受力情况.除受自身重力外,链条还 受到柱体半圆形表面的支持力.在柱体上部半圆形表面上的 任意点,该支持力必沿半径向外方向,用N,表示。链条受到 的支持力是方向随其作用点而变化的力系,简称支持力系 链条质心的运动由它所受到的重力和支持力系决定.为 h/2 建立链条质心运动方程,先分析链条质心位置(x,y)随其右 侧端点y坐标的变化规律.由如图所示的几何关系,可求得 链条质心的坐标为 -y+xco (1) 2 。= +yoo (2) 其中(x0,yo)是链条质心在开始时刻的位置,L(=h+πR)表 示链条的总长度.利用速度的定义,可从(1)和(2)式求得 质心的速度为 0,2R (3) ,=+-少2-2 -V L△tL△t (4) 其中)代表链条右端点速度(以向下为正向),其大小可由链条运动的机械能守恒关系求得 在链条下滑过程中只有重力做功,所以机械能守恒 (5) 由此可知 28y (6) 式中已同时考虑了)的方向. 由加速度的定义,从(6)式可求出链条右侧端点的加速度 中国科学技术大学物理学院叶邦角整理
三、(20 分) 不光滑水平地面上有一质量为 m 的刚性柱体,两者之间的摩擦因数记为μ.柱体 正视图如图所示,正视图下部为一高度为 h 的矩形,上部为一半径为 R 的半圆形.柱 体上表面静置一质量同为 m 的均匀柔软的链条,链条两端距地面的高度均为 h/2, 链条和柱体表面始终光滑接触.初始时,链条受到微小扰动而沿柱体右侧面下滑.试 求在链条开始下滑直至其右端接触地面之前的过程中,当题中所给参数满足什么关系 时, 1.柱体能在地面上滑动; 2.柱体能向一侧倾倒; 3.在前两条件满足的情形下,柱体滑动先于倾倒发生. 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理