物理奥林匹克竞赛：全国物理奥林匹克竞赛第33届复赛试题（含参考答案）

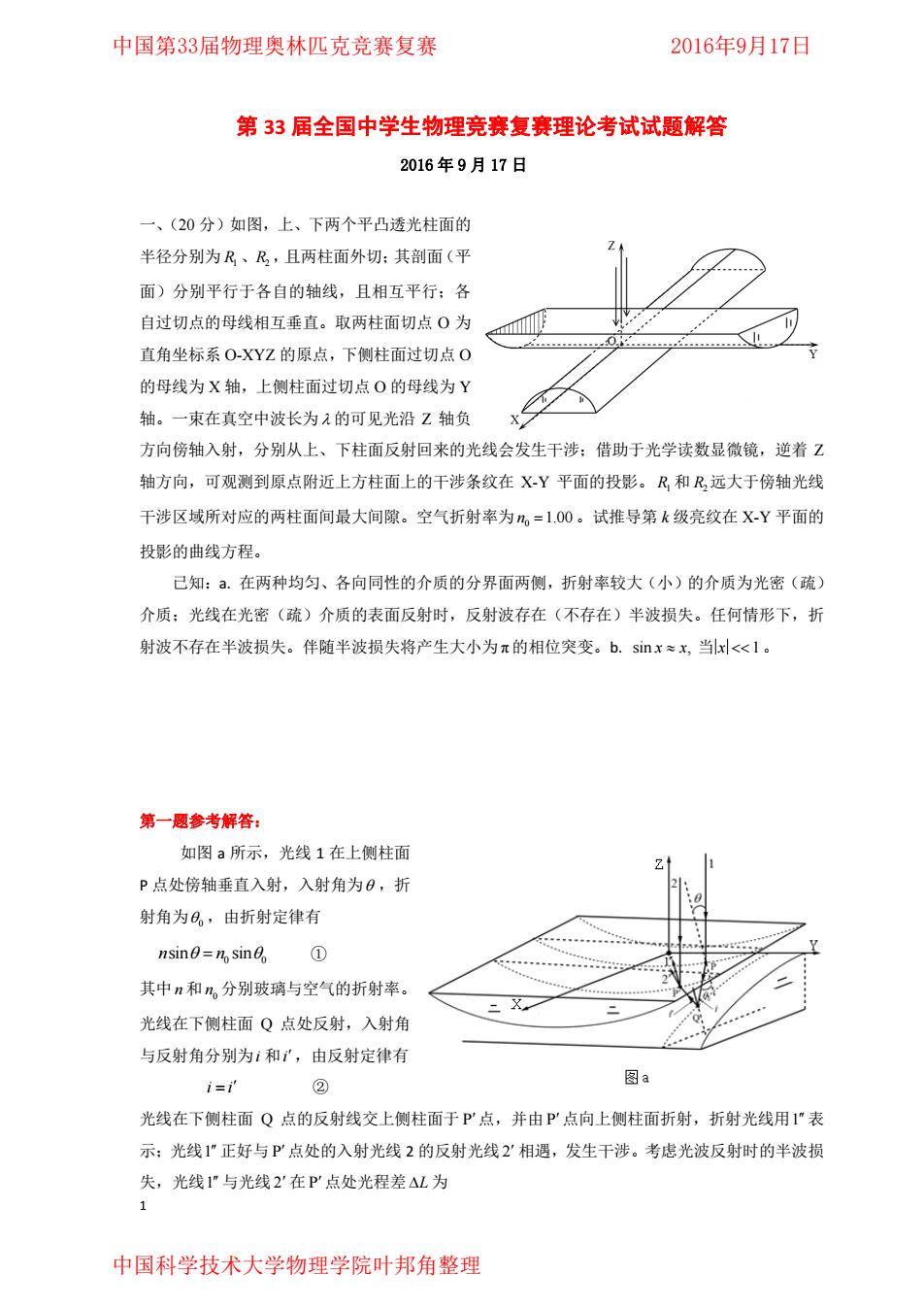
中国第33届物理奥林匹克竞赛复赛 2016年9月17日 第33届全国中学生物理竞赛复赛理论考试试题解答 2016年9月17日 一、(20分)如图，上、下两个平凸透光柱面的 半径分别为R、R,且两柱面外切：其剖面（平 面)分别平行于各自的轴线，且相互平行：各 自过切点的母线相互垂直。取两柱面切点O为 直角坐标系O-XYZ的原点，下侧柱面过切点O 的母线为X轴，上侧柱面过切点O的母线为Y 轴。一束在真空中波长为1的可见光沿Z轴负 方向傍轴入射，分别从上、下柱面反射回来的光线会发生干涉：借助于光学读数显微镜，逆着Z 轴方向，可观测到原点附近上方柱面上的干涉条纹在XY平面的投影。R和R远大于傍轴光线 干涉区域所对应的两柱面间最大间隙。空气折射率为m。=1.00。试推导第k级亮纹在X-Y平面的 投影的曲线方程。 己知：.在两种均匀、各向同性的介质的分界面两侧，折射率较大（小）的介质为光密（疏） 介质：光线在光密（疏）介质的表面反射时，反射波存在（不存在）半波损失。任何情形下，折 射波不存在半波损失。伴随半波损失将产生大小为π的相位突变。b.sinx≈x,当lx<1。 第一题参考解答： 如图a所示，光线1在上侧柱面 P点处傍轴垂直入射，入射角为0，折 射角为O,由折射定律有 nsin=n sin ① 其中n和n。分别玻璃与空气的折射率。 光线在下侧柱面Q点处反射，入射角 与反射角分别为i和，由反射定律有 i=i' ② 图a 光线在下侧柱面Q点的反射线交上侧柱面于P'点，并由P'点向上侧柱面折射，折射光线用1"表 示：光线1”正好与P点处的入射光线2的反射光线2'相遇，发生干涉。考虑光波反射时的半波损 失，光线1"与光线2'在P'点处光程差△L为 1 中国科学技术大学物理学院叶邦角整理

1  第 33 届全国中学生物理竞赛复赛理论考试试题解答 2016 年 9 月 17 日 一、（20 分）如图，上、下两个平凸透光柱面的 半径分别为 R1 、R2，且两柱面外切；其剖面（平 面）分别平行于各自的轴线，且相互平行；各 自过切点的母线相互垂直。取两柱面切点 O 为 直角坐标系 O-XYZ 的原点，下侧柱面过切点 O 的母线为 X 轴，上侧柱面过切点 O 的母线为 Y 轴。一束在真空中波长为 的可见光沿 Z 轴负 方向傍轴入射，分别从上、下柱面反射回来的光线会发生干涉；借助于光学读数显微镜，逆着 Z 轴方向，可观测到原点附近上方柱面上的干涉条纹在 X-Y 平面的投影。 R1 和 R2远大于傍轴光线 干涉区域所对应的两柱面间最大间隙。空气折射率为 0 n 1.00 。试推导第 k 级亮纹在 X-Y 平面的 投影的曲线方程。 已知：a.  在两种均匀、各向同性的介质的分界面两侧，折射率较大（小）的介质为光密（疏） 介质；光线在光密（疏）介质的表面反射时，反射波存在（不存在）半波损失。任何情形下，折 射波不存在半波损失。伴随半波损失将产生大小为 π 的相位突变。b.  sin , 1 xx x   当 。 第一题参考解答：       如图 a 所示，光线 1 在上侧柱面 P 点处傍轴垂直入射，入射角为 ，折 射角为0 ，由折射定律有 0 0 n n sin sin          ① 其中 n 和 0 n 分别玻璃与空气的折射率。 光线在下侧柱面 Q 点处反射，入射角 与反射角分别为i 和i，由反射定律有 i i            ② 光线在下侧柱面 Q 点的反射线交上侧柱面于 P点，并由 P点向上侧柱面折射，折射光线用1 表 示；光线1 正好与 P点处的入射光线 2 的反射光线 2 相遇，发生干涉。考虑光波反射时的半波损 失，光线1 与光线 2 在 P点处光程差 L 为 中国第33届物理奥林匹克竞赛复赛 2016年9月17日 中国科学技术大学物理学院叶邦角整理

中国第33届物理奥林匹克竞赛复赛 2016年9月17日 L=[-,+%(PQ+PO)+}M-,=%(0+PO)-M,-+子 ③ 式中入为入射光线在真空中的波长，n,=1.O0。由题意，R和R远大于傍轴光线干涉区域所对应 的两柱面间最大间隙：因而在傍轴垂直入射情况下有 0≈0，'=i<1 ①式成为 n0≈n8 ④ 亦即 1>9,≈n0≈0 ⑤ 在傍轴条件下，柱面上P、Q两处切平面的法线近似平行，因此 1>'=i≈0≈0 ⑥ 从而，在P、Q两处，不仅切平面的法线近似平行，而且在上下表面的反射光线、折射光线均近 似平行于入射线，因而也近似平行于Z轴，从而P'与P点近似重合，即 2p≈2p ⑦ 且PQ近似平行于Z轴，因而长度 p'Q≈PQ≈p-20 ⑧ 由③⑧式得 M=20+分=2%-+月 ⑨ 可以将⑨式右端的÷坐标近似用x或y-坐标表出。为此，引 入一个近似公式。如图b所示，设置于平面上的柱面透镜与平面之 间的空气隙的厚度为e,柱面半径为R。对三边边长分别为R、 R-e和r的直角三角形有 R2=(R-e)2+r2 ⑩ 即 2Re-e2=r2 ① 在光线傍轴垂直入射时，e<R,可略去①式 左端的e2,故 2 e=2R ② 在光线傍轴垂直入射时，前面己证近似有 PQ亿轴。故可将上、下两个柱面上的P、Q两 点的坐标取为P(x,,p)、Q(x,y,o),如图C 图c 中国科学技术大学物理学院叶邦角整理

2       p 0 p 0 p p ( ) (PQ P Q) ( ) (PQ P Q) ( ) 2 2 L n z n n z n nz z                                       ③ 式中 为入射光线在真空中的波长， 0 n 1.00 。由题意，R1 和 R2远大于傍轴光线干涉区域所对应 的两柱面间最大间隙；因而在傍轴垂直入射情况下有   0，i i   1 ①式成为 0 0 n n                                                        ④ 亦即 0 1 0     n                                                ⑤ 在傍轴条件下， 柱面上 P、Q 两处切平面的法线近似平行，因此 0 1 0     i i                                               ⑥ 从而，在 P、Q 两处，不仅切平面的法线近似平行，而且在上下表面的反射光线、折射光线均近 似平行于入射线，因而也近似平行于 Z 轴，从而 P与 P 点近似重合，即 p p z z                                                           ⑦ 且 PQ 近似平行于 Z 轴，因而长度 P Q PQ P Q    z z                                               ⑧ 由③⑧式得 0 0   P Q 2 PQ 2 2 2 L n nz z                     ⑨ 可以将⑨式右端的 z-坐标近似用 x- 或 y- 坐标表出。为此，引 入一个近似公式。如图 b 所示，设置于平面上的柱面透镜与平面之 间的空气隙的厚度为 e ，柱面半径为 R 。对三边边长分别为 R 、 R e  和 r 的直角三角形有   2 2 2 R Re r =   ⑩ 即 2 2 2Re e r   ⑪ 在光线傍轴垂直入射时， e R  ，可略去⑪式 左端的 2 e ，故 2 2 r e R  ⑫ 在光线傍轴垂直入射时， 前面已证近似有 PQ//Z 轴。故可将上、下两个柱面上的 P、Q 两 点的坐标取为 P P (, , ) x y z 、Q Q (, , ) x y z ，如图 c 中国第33届物理奥林匹克竞赛复赛 2016年9月17日 中国科学技术大学物理学院叶邦角整理

中国第33届物理奥林匹克竞赛复赛 2016年9月17日 所示。根据②式可知，P、Q两点到XOY切平面的距离分别为 x e=2m=2D,e2=-02 ③ 最后，光线在上、下两个柱面反射并相遇时，其光程差△L为 2m-+子-2%6+6)+号 若P、Q两点在XOY平面的投影点(x,y)落在第k级亮（暗）纹上，则△L须满足条件 k k=1,2,…,亮环 ⑤ (k+)2,k=0,1,2,…,暗环 ⑤式中亮环条件对应于第k级亮纹上的点(x,y,)的x、y-坐标满足的方程。 更具体地，不妨假设R>R,根据⑤式中的亮环条件，可得第k级亮纹的方程为 x2 y =1,k=12.… ⑥ ARB网 它们是椭圆亮环纹，其半长轴与半短轴分别为 4=Vk-2R%,k=l2,B=k-R1m,k=1,2, ⑦ 评分参考：①②式各1分，③式2分，④⑤式各1分，⑥式2分，⑦式1分，⑧式2分，⑨⑩①② 式各1分，③式2分，④式1分，⑤式（亮环条件正确）2分。 中国科学技术大学物理学院叶邦角整理

3  所示。根据⑫式可知，P、Q 两点到 XOY 切平面的距离分别为 2 1 P 1 2 x e z R   ， 2 2 Q 2 2 y e z R   ⑬ 最后，光线在上、下两个柱面反射并相遇时, 其光程差 L为     0P Q 01 2 2 2 2 2 L nz z ne e         2 2 2 2 0 0 1 2 1 2 2 22 2 2 x y xy n n R R RR                 ⑭ 若 P、Q 两点在 XOY 平面的投影点(, ) x y 落在第 k 级亮(暗)纹上，则 L须满足条件 2 2 0 1 2 , 1,2, , 1 2 ( ) , 0,1,2, , 2 k k x y L n R R k k                        亮环 暗环 ⑮ ⑮式中亮环条件对应于第 k 级亮纹上的点(, ,) x y z 的 x -、 y -坐标满足的方程。 更具体地，不妨假设 R R 1 2  ，根据⑮式中的亮环条件，可得第 k 级亮纹的方程为 2 2 2 2 1, 1,2 k k x y k A B    ⑯ 它们是椭圆亮环纹，其半长轴与半短轴分别为 1 0 1 ( ) / , 1,2, 2 A k Rnk k     ， 2 0 1 ( ) / , 1,2, 2 B k R nk k     ⑰ 评分参考：①②式各 1 分，③式 2 分，④⑤式各 1 分，⑥式 2 分，⑦式 1 分，⑧式 2 分，⑨⑩⑪⑫ 式各 1 分，⑬式 2 分，⑭式 1 分，⑮式（亮环条件正确）2 分。 中国第33届物理奥林匹克竞赛复赛 2016年9月17日 中国科学技术大学物理学院叶邦角整理

中国第33届物理奥林匹克竞赛复赛 2016年9月17日 二、(20分)某秋天清晨，气温为4.0℃，一加水员到 观 加水口 蒸馏水罐 实验园区给一内径为2.00m、高为2.00m的圆柱形不 锈钢蒸馏水罐加水。罐体导热良好。罐外有一内径为 柱 4.00cm的透明圆柱形观察柱，底部与罐相连（连接 处很短)，顶部与大气相通，如图所示。加完水后， 加水员在水面上覆盖一层轻质防蒸发膜（不溶于水， 与罐壁无摩擦)，并密闭了罐顶的加水口。此时加水 员通过观察柱上的刻度看到罐内水高为1.00m。 (1)从清晨到中午，气温缓慢升至24.0℃，问此时 观察柱内水位为多少？假设中间无人用水，水的蒸发及罐和观察柱体积随温度的变化可忽略。 (2)从密闭水罐后至中午，罐内空气对外做的功和吸收的热量分别为多少？求这个过程中罐内空 气的热容量。 己知罐外气压始终为标准大气压p。=1.01×10Pa,水在4.0℃时的密度为 Po=1.00×10kg·m3,水在温度变化过程中的平均体积膨胀系数为=3.03×10K,重力加速度 大小为g=9.80m·s2,绝对零度为-273.15℃。 第二题参考解答： (1)清晨加完水封闭后，罐内空气的状态方程为 PoVo=nRTo ① 式中n为罐内空气的摩尔数，P。、'。=πm3和T。=277.15K分别是此时罐内空气的压强、体积和 温度。 至中午时，由于气温升高，罐内空气压强增大，设此时罐内空气的压强、体积和温度分别为P、 V和T,相应的状态方程为 PV=nRT ② 式中T=297.15K。空气和水的体积都发生变化，使得观察柱中水位发生变化，此时观察柱内水 位和罐内水位之差为， △h=-业+-+(I-S+S4 ③ S S 式中右端第三项是由原罐内和观察柱内水的膨胀引起的贡献，1。=1.00m为早上加水后观测柱内 水面的高度，S=πm2、S2=4π×10m2分别为罐、观察柱的横截面积。由力平衡条件有 P=Po+Pg△h ④ 式中 中国科学技术大学物理学院叶邦角整理

4  二、（20 分）某秋天清晨，气温为 4.0 C ，一加水员到 实验园区给一内径为2.00 m 、高为2.00 m 的圆柱形不 锈钢蒸馏水罐加水。罐体导热良好。罐外有一内径为 4.00 cm 的透明圆柱形观察柱，底部与罐相连（连接 处很短），顶部与大气相通，如图所示。加完水后， 加水员在水面上覆盖一层轻质防蒸发膜（不溶于水， 与罐壁无摩擦），并密闭了罐顶的加水口。此时加水 员通过观察柱上的刻度看到罐内水高为1.00 m 。 （1）从清晨到中午，气温缓慢升至 24.0 C ，问此时 观察柱内水位为多少？假设中间无人用水，水的蒸发及罐和观察柱体积随温度的变化可忽略。 （2）从密闭水罐后至中午，罐内空气对外做的功和吸收的热量分别为多少？求这个过程中罐内空 气的热容量。 已知罐外气压始终为标准大气压 5 0 p   1.01 10 Pa ，水在 4.0 C 时的密度为 3 3 0  1.00 10 kg m   ，水在温度变化过程中的平均体积膨胀系数为 4 1  3.03 10 K    ，重力加速度 大小为 2 g 9.80m s   ，绝对零度为 273.15 C 。 第二题参考解答： （1）清晨加完水封闭后，罐内空气的状态方程为 00 0 p V nRT  ① 式中n 为罐内空气的摩尔数， 0 p 、 3 0 V  π m 和 0 T  277.15K 分别是此时罐内空气的压强、体积和 温度。 至中午时，由于气温升高，罐内空气压强增大，设此时罐内空气的压强、体积和温度分别为 1 p 、 V1和T1 ，相应的状态方程为 11 1 p V nRT  ② 式中 1 T  297.15K 。空气和水的体积都发生变化，使得观察柱中水位发生变化，此时观察柱内水 位和罐内水位之差为， 1 0 1 0 1 0 1 20 12 2 V V V V T T S Sl ( )( + ) h SS S       ③ 式中右端第三项是由原罐内和观察柱内水的膨胀引起的贡献， 0l 1.00 m 为早上加水后观测柱内 水面的高度， 2 1 S  π m 、 4 2 2 S 4π 10 m   分别为罐、观察柱的横截面积。由力平衡条件有 1011 p p gh    ④ 式中 中国第33届物理奥林匹克竞赛复赛 2016年9月17日 中国科学技术大学物理学院叶邦角整理

中国第33届物理奥林匹克竞赛复赛 2016年9月17日 Po P=1+k(C,-T) ⑤ 是水在温度为T时的密度。联立①②③④⑤式得关于△h的一元二次方程为 P,gS(△h2+(p,S+7P,g)△h-(÷-2p,。=0 T 式中 S'=-SS,2=1-K(T-7) ⑦ S+S2 解方程⑥得 -(PoS,+p 8Vo)+ (PoS,+ip8)+4p8SpV() △h= -=0.812m ⑧ 2pgS 另一解不合题意，舍去。由③⑤⑦⑧式和题给数据得 V,-'%=S△h-k(T-T)S,l=-0.0180m3 由上式和题给数据得，中午观察柱内水位为 4=h-:6+h=182m ⑨ S (2)先求罐内空气从清晨至中午对外所做的功。 (解法一)早上罐内空气压强P。=1.01×10Pa:中午观察柱内水位相对于此时罐内水位升高 △h,罐内空气压强升高了 p=PgAh=7.913×103Pa=7.91×103Pa ⑩ 由于△p<P。,可认为在准静态升温过程中，罐内空气平均压强为 p=P+。p=1.0495×103Pa=1.05×10Pa ⊙ 2 罐内空气体积缩小了 △'=0.0180m3 ② 可见△V/。<1,这说明①式是合理的。罐内空气对外做功 W=pAV=-1.889×103J=-1.9×103J ⑧ (解法二)缓慢升温是一个准静态过程，在封闭水罐后至中午之间的任意时刻，设罐内空气 都处于热平衡状态，设其体积、温度和压强分别为V、T和p。水温为T时水的密度为 Po P=1+K(T-T) ⑩ 将②③④式中的Y、T和p换为V、T和p,利用⑩式得，罐内空气在温度为T时的状态方程为 中国科学技术大学物理学院叶邦角整理

5  0 1 1 0 1( ) T T       ⑤ 是水在温度为T1 时的密度。联立①②③④⑤式得关于 h 的一元二次方程为 2 1 1 01 1 0 00 0 () ( ) ( ) 0 T gS h p S gV h p V T            ⑥ 式中 1 2 1 2 S S S S S    ， 1 0  1( )    T T ⑦ 解方程⑥得 2 1 01 1 0 01 1 0 1 00 0 1 ( ) ( )4 ( ) 0.812m 2 T p S gV p S gV gS p V T h gS               ⑧ 另一解不合题意，舍去。由③⑤⑦⑧式和题给数据得 3 1 0 1 0 10 V V S h T T Sl        ( ) 0.0180m 由上式和题给数据得，中午观察柱内水位为 1 0 1 0 1 + 1.82m V V lh l S     ⑨ （2）先求罐内空气从清晨至中午对外所做的功。 （解法一）早上罐内空气压强 5 0 p   1.01 10 Pa ；中午观察柱内水位相对于此时罐内水位升高 h ，罐内空气压强升高了                3 3 1      p gh  7.913 10 Pa 7.91 10 Pa                          ⑩ 由于 0   p p ，可认为在准静态升温过程中，罐内空气平均压强为 5 5 0 1 1.0495 10 Pa 1.05 10 Pa 2 pp p                         ⑪ 罐内空气体积缩小了 3   V 0.0180m                                                   ⑫ 可见 0   V V/ 1，这说明⑪式是合理的。罐内空气对外做功 3 3 W pV       1.889 10 J 1.9 10 J                       ⑬ （解法二）缓慢升温是一个准静态过程，在封闭水罐后至中午之间的任意时刻，设罐内空气 都处于热平衡状态，设其体积、温度和压强分别为V 、T 和 p 。水温为T 时水的密度为 0 0 1( ) T T       ⑩ 将②③④式中的V1、T1 和 1 p 换为V 、T 和 p ，利用⑩式得，罐内空气在温度为T 时的状态方程为 中国第33届物理奥林匹克竞赛复赛 2016年9月17日 中国科学技术大学物理学院叶邦角整理