
中国科学技术大学物理学院叶邦角整理 第32届全国中学生物理竞赛决赛理论考试评分标准 本卷可能需要用到下列公式: 广空-h:会-2+c:n+小-亏hx1 一、(15分)一根轻杆两端通过两根轻质弹簧A和B悬挂在天花 板下,一物块D通过轻质弹簧C连在轻杆上:A、B和C的劲度 系数分别为k、k,和k,D的质量为m,C与轻杆的连接点到A 和B的水平距离分别为α和b;整个系统的平衡时,轻杆接近水 平,如图所示。假设物块D在竖直方向做微小振动,A、B始终 6 可视为竖直,忽略空气阻力。 (1)求系统处于平衡位置时各弹簧相对于各自原长的仲长: (2)求物块D上下微小振动的固有频率: (3)当a和b满足什么条件时,物块D的固有频率最大?并求 Dm 出该固有频率的最大值。 参考解答: (1)沿竖直方向建立如图所示的坐标轴o.x。设三根弹簧 A、B和C的原长分别为1、1,和1,不妨设1,>1。设系 统处于平衡位置时,三根弹簧A、B和C相对于各自原长 的伸长分别为△x,、△x,和△x,。此时物块D处于平衡状态; 有 mg=k,△x3 即 4 ② AXE k E 设此时弹簧A和B的末端对轻杆的拉力分别为F和 mg £,。以弹簧C与轻杆的连接点为支点,由力矩平衡有 Fa=Fb ③ 竖直方向轻杆所受合力为零,有 F+F-mg=0 ④ 由胡克定律有 F=k△r ⑤ F2=k2△x ⑥ 由③④⑤⑥式得 4此-mgb ⑦ (a+b)k 11g0 △x,=(a+bk, ⑧ (2)挂上物块D之前,系统平衡时弹簧C的木端E点的坐标x为 x=(+4+) ⑨ a+b 挂上物块D后,系统重新处于半衡位置时,弹簧C的木端从E点移动到E'点。E点的坐 标x为 x=+A+h+△x3+a+A-4x) ⑩ a+b 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 将系统视为一等效弹簧,则系统处于静平衡时等效弹簧仲长为 AX:=x=A+r +a(r,Ar) ① a+b 将②⑦⑧式代入①式,得到系统处于静平衡时等效弹簧的伸长为 Axr =mg(a'k +bk)mg 1② (a+b)kk,k 因此等效弹簧的等效劲度系数为 (a+b)'kk k ③ a'k k+b'kk+(a+b)'k k 系统的固有频率为 (a+b)k kks .=mmlakkj+bk.k,+(a+b)'k.k:] ④ (3)由4@=0,有 da a=点6 ③ k 此时 d'=_m 6 da' (k+k)k+飞+k) 因此⑤式为系统尚有频率取最人值的条件,其最人固有频率的值为 (k+k2)ks 0三 ① (k+kz +k)m 评分标准: 第(1)问8分,①2③④⑤⑥⑦⑧式各1分 第(2)问4分,①②3④式各1分: 第(3)问3分,⑤⑥①式各1分. 二、(20分)如图,轨道型电磁发射器是山两条平行固定长直刚性金属导轨、高功率电源、 接触导电性能良好的电枢和发射体等构成。电流从电流源输出,经过导轨、电枢和另~条导 轨构成闭合回路,在空问中激发磁场。载流电枢在安培力作用下加速,推动发射体前进。已 比枢质量为m,发射体质量为m,:导轨单位长度的比阻为R,导轨每增加单位长度整个 回路的电感的增加量为,;电枢引入的电阻为R、电感为L,;回路连线引入的电阻为R,、 电感为L。导轨与电枢间摩擦以及空气阻力可忽略。 (1)试画出轨道型比磁发射器的等效比路图,并给出回路方程: (2)求发射体在导轨屮运动加速度的大小与可路电流的关系: (3)设回路比流为恒流I(平顶脉冲地流)、电枢和发射休的总质量为m,+m。=0.50kg、 导轨长度为x=500m、导轨.上单位长度电感增加量L,=1.0H/m,若发射体开始时静止, 山口速度为vm=3.0×103m/s,,求回路电流1和加速时间x。 中国科学技术大学物理学院叶邦角整理
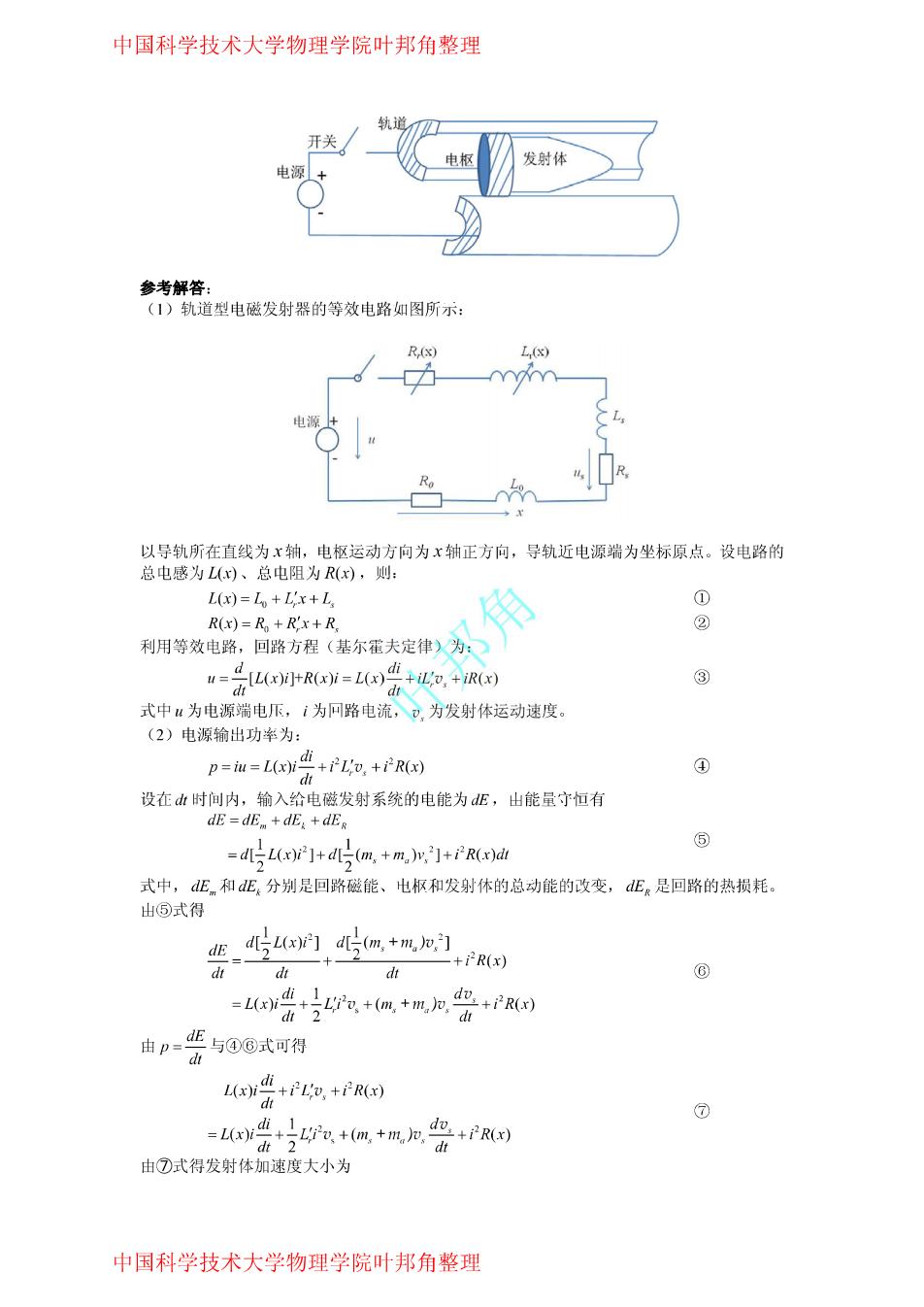
中国科学技术大学物理学院叶邦角整理 轨道 开关 电枢 发射体 电源 参考解答: (1)轨道型电磁发射器的等效电路如图所示: R(x) L,(x) 以导轨所在直线为x轴,电枢运动方向为x轴正方向,导轨近电源端为坐标原点。设电路的 总电感为L(心)、总电阻为R(x),则: L(x)=Lo+L'x+L ① R(x)=R+Rx+R ② 利用等效电路,回路方程(基尔霍夫定律)为: u=4L(x)i+R(x)i=L(x)+iL,+iR(x) ③ d dt 式中u为电源端电压,i为回路电流,。,为发射体运动速度。 (2)电源输出功率为: p=iu=L)i +2Lo,+R(x) ④ dt 设在d山时间内,输入给电磁发射系统的电能为dE,山能量守恒有 dE =dE+dE+dEg ⑤ -dL()]+d (m+m)v,]+R(x)di 式中,dE和dE分别是回路磁能、枢和发射体的总动能的改变,dE。是回路的热损耗。 出⑤式得 dE d5L(x)]d5m,+,力,] +2R(x) d dt dt ⑥ =L(x)idi 1 +'0,+(m,+m,加, dt 2 do+i平R(x) 由p=E与④⑥式可得 L)i+PL+PR() dt =L)idi1 ⑦ 而++m+m,加多+ dt 由⑦式得发射体加速度大小为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 1 、L2 ⑧ dt2(m、+m (3)若回路电流为恒流I,则电枢和发射体在时刻1的加速度、速度和位移的大小分别为 a=d地= 1 LP dt2(m。+m,) ⑨ L12 0、=a,f= ⑩ 2(m。+m,) 1 L72 x=21= 一2 ① 4(m。+m,) 要使发射体山口速度m达到3.0×103ms,则由题给数据得 9.0×10 dom= m/s2=9.0×103ms3 1② 2Xsm 2×5.0 H⑨2式得 2(m。+ma)am 2×0.50×9.0×106 A=3.0×10°A L 1.0×10-6 加速时间为 T=D=3.0x103 s=3.3×10-4s ④ am9.0×105 评分标准:第(1)问7分,等效电路图正确给3分,①②式各1分,③式2分: 第(2)问8分,④⑤⑥式各2分,⑦⑧式各1分: 第(3)问5分,⑨⑩①3④式各1分。 二、(15分)俄国火箭专家齐奥尔科夫斯基将火箭发射过程进行模型简化,得出了最早的理 想火箭方程,为近代火箭、导弹T程提供了理论依据。该简化模型为:待发射火箭静止于惯 性参考系S中某点,忽略火箭所受的地球引力等外力的作刀,火箭(包含燃料)的初始静 止质量为M,;在=0时刻点火,火箭向左排出气休,气体相对于火箭的速度恒为'。,使火 箭向右发射:在S系中观测,火箭的速度为,排出气体的速度为V,,如图所示。根据此 模型,火箭运行一段时间后,当其静止质量山M,变为M时, (1)用牛顿力学推导火箭所获得的速度V与质量比M/M,之间的关系: (2)用狭义相对论力学推导火箭所获得的速度Y与质量比M/M,之间的关系: (3)当Y远小于真空中的光速c时,计算以上两种结果之差,保留至(化/c)项。 V(相对丁火箭) '(相对于S系) (相对于S系) M 参考解答: (1)用牛顿力学求火箭获得的速度与质量比率之间的关系。 根据动量守恒定律,火箭动量的变化等于排出质量为dm的气体引起的动量的变化 d(MV)=V,dm ① 由质量守恒定律得 dMdm =0 ② 由速度叠加原理有 2='。- ③ 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 将③式代入①式得 d(M')=('-')dm ④ 将②式代入④式得 dM=_dy ⑤ M V. 两边取积分得 此兴 ⑥ 利用题给积分公式完成积分,并考虑初始条件,得 n-上 ⑦ M,' 或 M y=-'ln。 ⑧ “M (2)用狭义相对论求火箭获得的速度与质量比率之间的大系。 根据相对论动量守恒定律,火箭动量的变化等于排出质量为dm的气体引起的动量变化 d MV )= dm ⑨ v1-V2/c v1-V2/c2 根据相对论能量守恒定律,火箭能量的减少等于排山质量dm的气休对应的能量 Me2 an-vl dme2 ⑩ 邦角 V1-1c 中相对论速度叠加原理有 y。- V,=1-W.19 ① 将①式代入⑨式并利用⑩式得 d(- d(- ② 1-1c 1-vV.lc;-v2lc 此即 dM dv 图 MV.1-V21c2) 对③式两边积分,并利用恒等式 品) 1 得 兴e ④ 利用题给积分公式完成积分,并考虑初始条件,得 5 或 6 或 5=1-(M/M)ě 1+M/M)产 ⑩ 中国科学技术大学物理学院叶邦角整理