
静力学力对点的矩的矢量计算式为:mo(F) =r×F(. mo(F) -|Fl sin(r, F) -F ·h)力对点的矩等于矩心到该力作用点的矢径与该力的矢量积。r=xi+yji+zk由于F= Xi+Yi+Zk[m,(F)]. = yz - zY[ijk]..mo(F)=rxF=x y =[m,(F)], = zX - xzXYZ[m,(F) = xY - yX=(yZ-zY)i+(2X -xZ)j+(xY-yX)k-[mo(F)],i+[mo(F)], j+[mo(F)].k11
11 力对点的矩等于矩心到该力作用点的矢径与该力的矢量积。 ( ( ) sin( , ) ) ( ) , m F r F r F F h m F r F O O = = = 由于F =Xi +Yj+Zk r =xi + yj+zk X Y Z x y z i j k mO (F )=rF = m F i m F j m F k yZ zY i zX x Z j x Y yX k O x O y O z [ ( )] [ ( )] [ ( )] ( ) ( ) ( ) = + + = − + − + − 力对点的矩的矢量计算式为: m F xY yX m F zX xZ m F yZ zY o z o y o x = − = − = − ( ) ( ) ( )
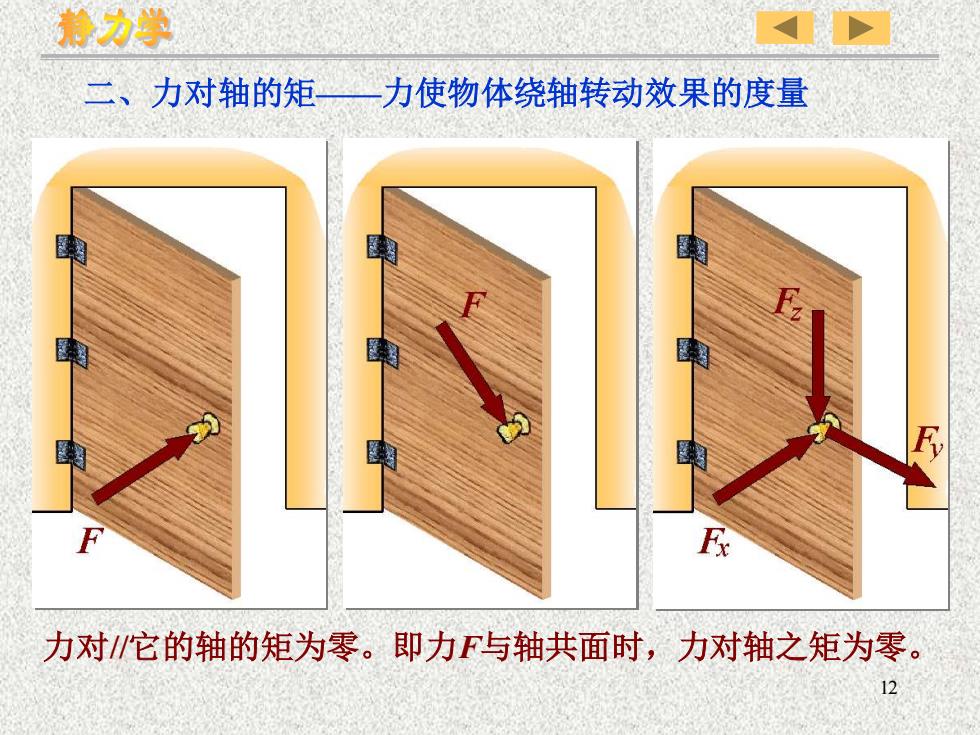
静力学三、力对轴的矩力使物体绕轴转动效果的度量WFFx力对/它的轴的矩为零。即力F与轴共面时,力对轴之矩为零12
12 二、力对轴的矩——力使物体绕轴转动效果的度量 力对//它的轴的矩为零。即力F与轴共面时,力对轴之矩为零
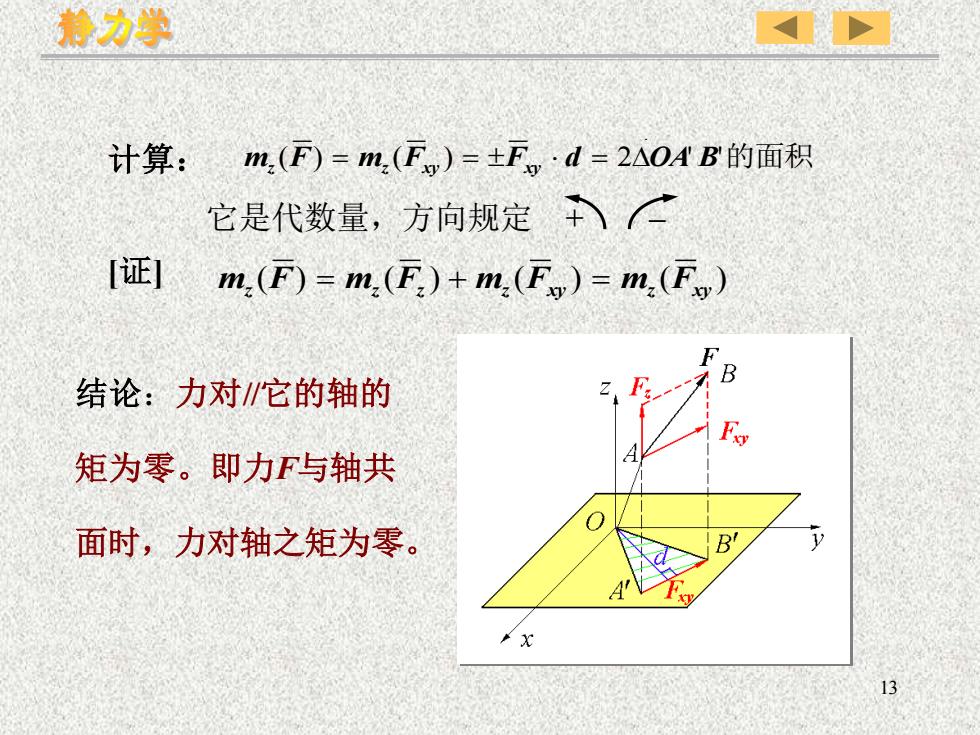
静力学计算:m(F)=m(F)=+Fd =2△OA B的面积它是代数量,方向规定 ([证] m,(F) = m(F) + m,(F,) = m,(F)B结论:力对/它的轴的2矩为零。即力F与轴共V面时,力对轴之矩为零。13
13 计算: 它是代数量,方向规定 + – mz (F) = mz (Fxy ) = Fxy d = 2OA' B'的面积 结论:力对//它的轴的 矩为零。即力F与轴共 面时,力对轴之矩为零。 ( ) ( ) ( ) ( ) mz F = mz Fz + mz Fxy = mz Fxy [证]

静力学三、力对点的矩与力对通过该点的轴之矩的关系: m,(F) = m,(F,) = m,(F)FP- Yx - XyF.[m,(F)]. = yz - zy又:[m,(F)], - zX - xz2[m,(F)] = xY - yX:. [mo(F)], = m (F)m,(F) = [m,(F)同理:m,(F) =-[m,(F)]14
14 [m (F)] m (F) O z = z 三、力对点的矩与力对通过该点的轴之矩的关系 Yx Xy mz F mz Fxy mo Fxy = − ( ) = ( ) = ( ) 又: m F xY yX m F zX xZ m F yZ zY o z o y o x = − = − = − ( ) ( ) ( ) 同理: y o y x o x m F m F m F m F ( ) ( ) ( ) ( ) = =

静力学又由于 mo(F)=rxF-[mo(F)],i+[mo(F)],j+[mo(F)]_k.. m,(F) = m,(F)i + m,(F)j + m,(F)k力对点O的矩为:大小:mo(F)-/(m,(F)2 +(m,(F)2 +(m.(F)2m,(F)m.(F)m.(F),cosB-cosa方向:COSYmo(F)mo(F)mo(F)
15 mo (F) = mx (F)i + my (F) j + mz (F)k m F r F m F i m F j m F k O O x O y O z 又由于 ( )= =[ ( )] +[ ( )] +[ ( )] 力对点O的矩为: 2 2 2 m (F) (m (F)) (m (F)) (m (F)) 大小: O = x + y + z ( ) ( ) ,cos ( ) ( ) ,cos ( ) ( ) cos m F m F m F m F m F m F O z O y O x 方向: = = =