
静力学三、空间汇交力系的平衡空间汇交力系平衡的充要条件是:力系的合力为零,即:X=0即:R-F-0空间汇交力系的平衡方程ZY=0z=0[例1已知: AB=3m,AE=AF-4m,O-20kN求:绳BE、BF的拉力和杆AB的内力y解:分别研究C点和B点作受力图HTi'X由C点:ZY=0,T'sin15°-Qsin45°=0oQ45°..T -546(kN)QMi
6 三、空间汇交力系的平衡: R =Fi =0 空间汇交力系平衡的充要条件是:力系的合力为零,即: X =0 Y =0 Z =0 即: 空间汇交力系的平衡方程 [例] 已知:AB=3m,AE=AF=4m, Q=20kN; 求:绳BE、BF的拉力和杆AB的内力 解:分别研究C点和B点作受力图 546(kN) 0, 'sin15 sin45 0, 1 1 = = − = T 由C点: Y T Q
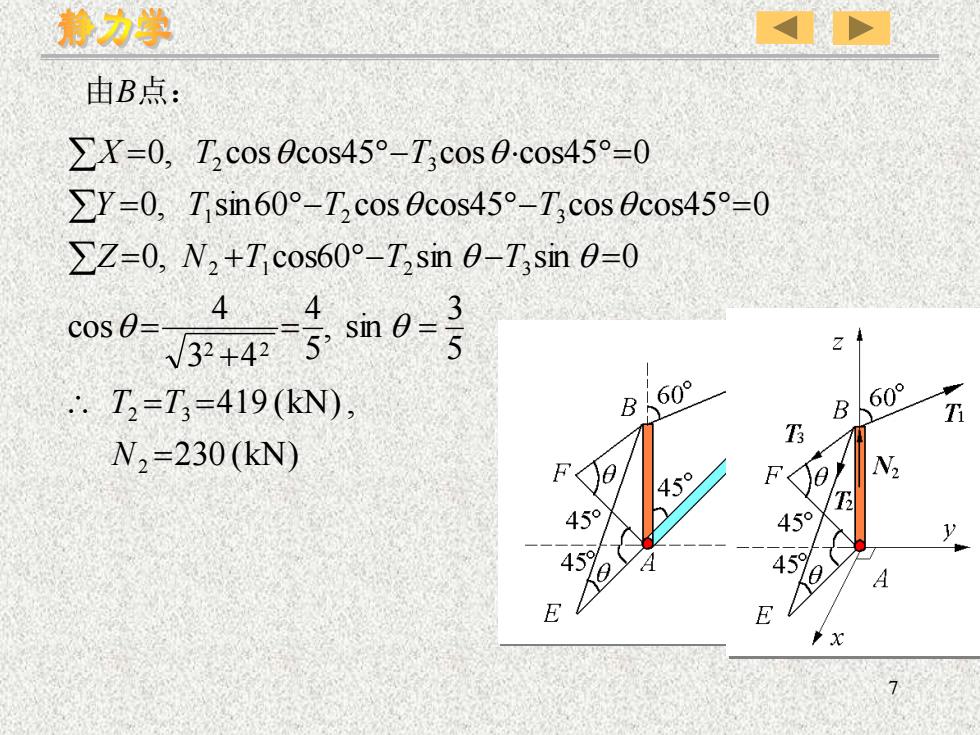
静力学由B点:ZX=0, T, cos Ocos45°-T,cos O-.cos45°=0ZY =0, T, sin60°-T, cos Ocos45°-T,cos cos45°=0Z=0, N,+T cos60°-T,sin 0-T,sin 0=0443cos O=V32 +4273: sin 0 =5ZBL60°60°T, =T,-419(kN),BTiT3N,=230 (kN)N2F0F<014545945°y45%4506ADEE/ x7
7 230 (kN) 419 (kN), 5 3 , sin 5 4 3 4 4 cos 0, cos60 sin sin 0 0, sin60 cos cos45 cos cos45 0 0, cos cos45 cos cos45 0 2 2 3 2 2 2 1 2 3 1 2 3 2 3 = = = = = + = = + − − = = − − = = − = N T T Z N T T T Y T T T X T T 由B点:
静力学$4-2空间力偶系空间力偶及其矢量表示:400N400N空间力偶三要素:大小、1000N转向,力偶的作用面021所以空间力偶矩必须用0.5m量表示(b)(C)(a)图4-10力偶的平行移动m力偶的转向为右手螺旋法则。F空间力偶是一个自由矢量FY8
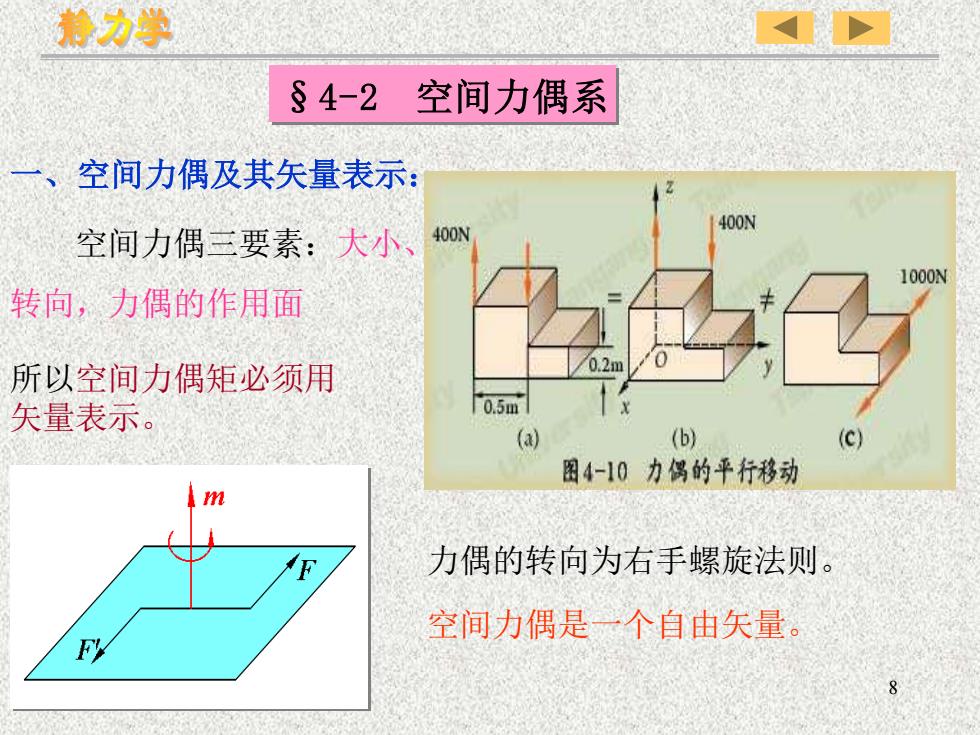
8 §4-2 空间力偶系 空间力偶三要素:大小、 转向,力偶的作用面 一、空间力偶及其矢量表示: 力偶的转向为右手螺旋法则。 空间力偶是一个自由矢量。 所以空间力偶矩必须用 矢量表示

静力学一、空间力偶的等效定理作用在同一刚体的两个力偶,若它们的力偶矩矢的相等,则两个力偶等效。由此可得出,空间力偶矩是自由矢量,它有三个要素:①力偶矩的大小=m②力偶矩的方向与力偶作用面法线方向相同③转向遵循右手螺旋规则。三、空间力偶系的合成与平衡nLm1、合成:m-m+m +...+m.1ilZw*=02、平衡: m=m,-0Zw=0投影式为:w=0O
9 二、空间力偶的等效定理 作用在同一刚体的两个力偶,若它们的力偶矩矢的相等,则 两个力偶等效。 由此可得出,空间力偶矩是自由矢量,它有三个要素: ①力偶矩的大小= ②力偶矩的方向——与力偶作用面法线方向相同 ③转向——遵循右手螺旋规则。 m 三、空间力偶系的合成与平衡 = = + + + = n i m m m mn mi 1 1、合成: 1 2 2、平衡: = =0 m mi 投影式为: mx =0 my =0 mz =0

静力学$·4-3力对点的矩与力对轴的矩一、力对点的矩的失量表示P3在平面:力对点的矩是代数量RP在空间:力对点的矩是矢量。[例]汽车反镜的球铰链B12-M. (F)大小:M。(F)=F·h=2ZAOB面积RTA(xy.z)量方位:作用面法线位置箭头指向:力矩转向(右手螺旋法则)图4-8力对点之矩10
10 在平面:力对点的矩是代数量。 在空间:力对点的矩是矢量。 [例] 汽车反镜的球铰链 §4-3 力对点的矩与力对轴的矩 一、力对点的矩的矢量表示 大小: MO (F) = F h = 2AOB面积 矢量方位:作用面法线位置 箭头指向:力矩转向 (右手螺旋法则)