
To begin with,we define a distinguished circulant matrix W with first row (0,1,0,...,0).W is just the identity matrix with its top row moved to the bottom,e.g.for n =4, 0 100 0 0 1 0 0 0 0 1 0 01 0 0 01 1 0 00 W= W2= 0 W3= 0 0 01 0 0 0 0 1 0 0 100 0 10 100 0 001 Direct checking shows that i)Note that WT =W-1 (i.e.W is an orthogonal matrix). ii)The characteristic polynomial for W is p(t)=det(tI-W)=t"-1, and hence the eigenvalues of w are the nth roots of unity. i)For each nth root of unity入,vx=(1,入,2,.,λn-1)is an associated eigenvector
To begin with, we define a distinguished circulant matrix W with first row (0, 1, 0, . . . , 0). W is just the identity matrix with its top row moved to the bottom, e.g. for n = 4, W = 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 , W2 = 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 , W3 = 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 . Direct checking shows that i) Note that WT = W−1 (i.e. W is an orthogonal matrix). ii) The characteristic polynomial for W is p(t) = det(tI − W) = t n − 1, and hence the eigenvalues of W are the nth roots of unity. iii) For each nth root of unity λ, vλ = (1, λ, λ2 , . . . , λn−1 ) is an associated eigenvector

If C is any n x n circulant matrix,use its first row [ao a1 a2...an-1 to define a polynomial q(t)=ao+ait+azt2+...+an-1tn-1. i)Then C=q(W)=aoI+aW+a2W2+...+an-1wn-1. For example,when n=4, ao 0 0 0 [0 al 0 0 0 ao 0 0 0 0 0 aol al 0 aiW= ao 0 0 ai 0 0 aol 0 0 0 8 0 02 0 「0 0 0 a3 a2W2 0 3 0 0 0 0 a3w3 = as 0 00 0 a2 0 0 0 0 a3 0
If C is any n × n circulant matrix, use its first row [a0 a1 a2 . . . an−1] to define a polynomial q(t) = a0 + a1t + a2t 2 + · · · + an−1t n−1 . i) Then C = q(W) = a0I + a1W + a2W2 + · · · + an−1Wn−1 . For example, when n = 4, a0I = a0 0 0 0 0 a0 0 0 0 0 a0 0 0 0 0 a0 , a1W = 0 a1 0 0 0 0 a1 0 0 0 0 a1 a1 0 0 0 a2W2 = 0 0 a2 0 0 0 0 a2 a2 0 0 0 0 a2 0 0 , a3W3 = 0 0 0 a3 a3 0 0 0 0 a3 0 0 0 0 a3 0
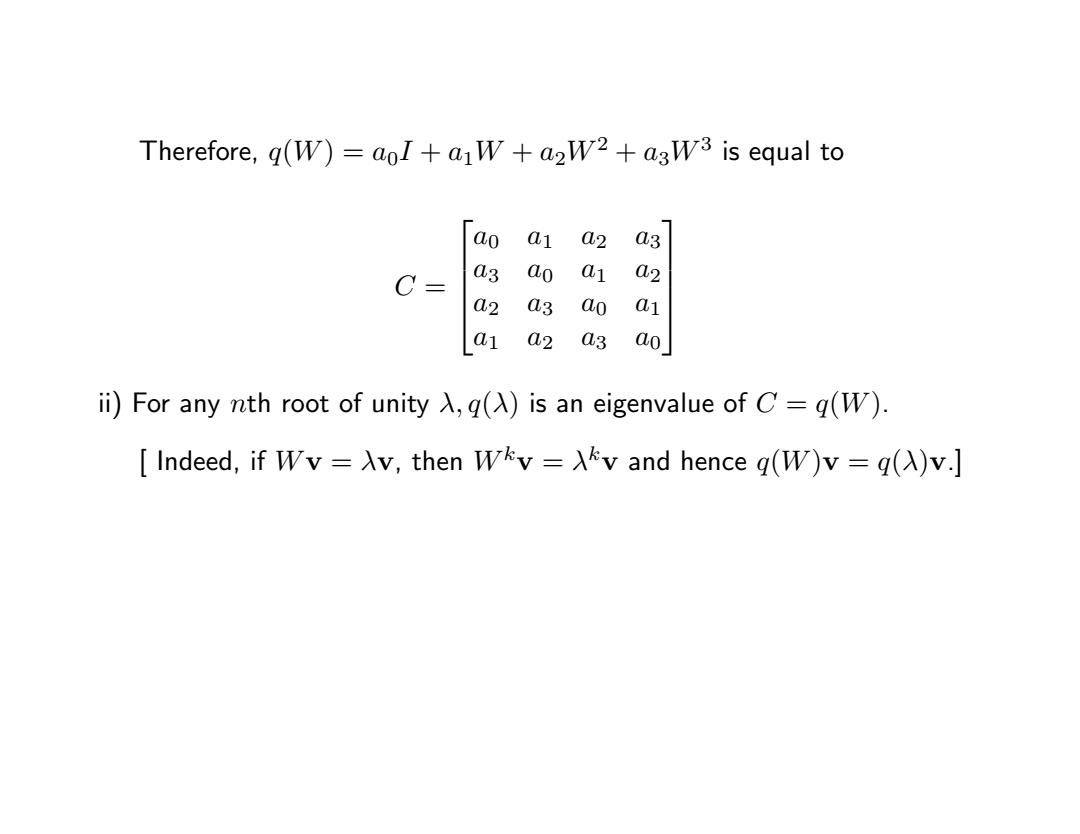
Therefore,g(W)=aoI+aW a2W2+a3W3 is equal to ao a1 a2 a3 C= a3 ao a1 a2 a2 03 ao a1 a1 a2 a3 ao i))For any nth root of unity入,q()is an eigenvalue of C=q(W) Indeed,if Wv=Av,then Wkv=Av and hence g(W)v=g(A)v.]
Therefore, q(W) = a0I + a1W + a2W2 + a3W3 is equal to C = a0 a1 a2 a3 a3 a0 a1 a2 a2 a3 a0 a1 a1 a2 a3 a0 ii) For any nth root of unity λ, q(λ) is an eigenvalue of C = q(W). [ Indeed, if Wv = λv, then Wkv = λ kv and hence q(W)v = q(λ)v.]

Example 3.Consider the circulant matrix [1 213 3 1 1 2 C= 1 31 2 2 13 1 Read the polynomial g from the first row of C: q(t)=1+2t+t2+3t3
Example 3. Consider the circulant matrix C = 1 2 1 3 3 1 2 1 1 3 1 2 2 1 3 1 . Read the polynomial q from the first row of C: q(t) = 1 + 2t + t 2 + 3t 3

Here,with n =4,the nth roots of unity are t1 and ti. The eigenvalues of C are now computed as q(1)=7,q(-1)=-3,q(i)=-i,andq(-i)=i. The corresponding eigenvectors are w(1) 三 (1,1,1,1), w(-1) 三 (1,-1,1,-1), v(i) = (1,i,-1,-i),and v(-) 上 (1,-i,-1,2) Can check that the characteristic polynomial of C is det(tI-C)=p(t)=t4-4t3-20t2-4t-21
Here, with n = 4, the nth roots of unity are ±1 and ±i. The eigenvalues of C are now computed as q(1) = 7, q(−1) = −3, q(i) = −i, and q(−i) = i. The corresponding eigenvectors are v(1) = (1, 1, 1, 1), v(−1) = (1, −1, 1, −1), v(i) = (1, i, −1, −i), and v(−i) = (1, −i, −1, i). Can check that the characteristic polynomial of C is det (tI − C) = p(t) = t 4 − 4t 3 − 20t 2 − 4t − 21