电路学习指导 第三章电阻电路的一般分析 I=I-U,s0R-U U 018: In Figa the mesh current equations are 21-2=U+U I: -21481,=-2U and U1=2I1 Then we get 4o Rab-13 E3-6 The circuit is shown as Fig.E3-6,write the mesh current equations.Where Usi=50V, Us3=30V,Is2=2A 20 白sx 109 509 (a) Fig.E3-6 Solution Method 1 chose the traveling direction as Fig.a 11:(20+20+10)I11-10I12-20I13=0 12: -20I11+(10+40)I12+U=Us1 13: -20111+(20+50)I13-U=-Us3 and 【s2=13-I12=2A: Method 2 chose the traveling direction as Fig.b 11:(20+20+10)11+20112-201130 12:20111+20+5040112+50113=Us1-Us 13 I12-2A E3-7 The circuit is shown as Fig.E3-7,find the branch current using loop current analysis. 26
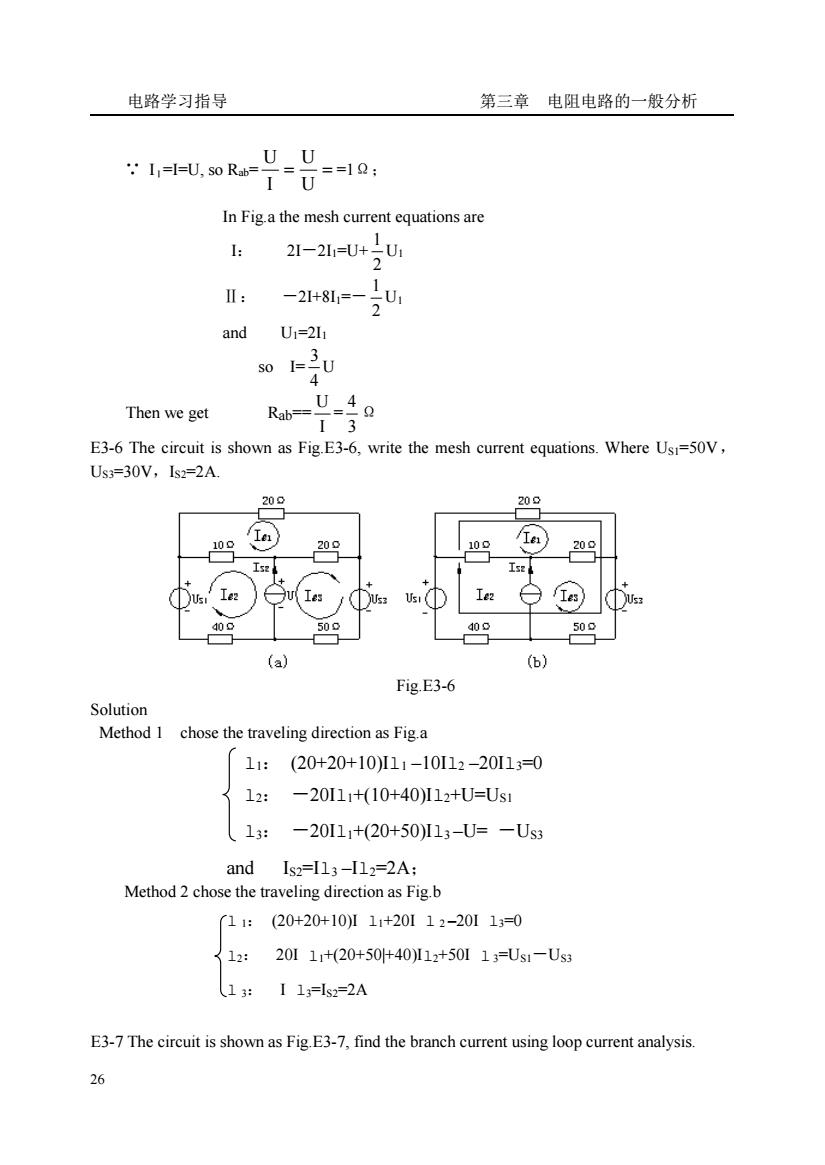
电路学习指导 第三章 电阻电路的一般分析 26 ∵ IⅠ=I=U, so Rab= = = U U I U =1Ω; In Fig.a the mesh current equations are I: 2I-2I1=U+ 2 1 U1 Ⅱ: -2I+8I1=- 2 1 U1 and U1=2I1 so I= 4 3 U Then we get Rab== I U = 3 4 Ω E3-6 The circuit is shown as Fig.E3-6, write the mesh current equations. Where US1=50V, US3=30V,IS2=2A. Fig.E3-6 Solution Method 1 chose the traveling direction as Fig.a l1: (20+20+10)Il1 –10Il2 –20Il3=0 l2: -20Il1+(10+40)Il2+U=US1 l3: -20Il1+(20+50)Il3 –U= -US3 and IS2=Il3 –Il2=2A; Method 2 chose the traveling direction as Fig.b l 1: (20+20+10)I l1+20I l 2 –20I l3=0 l2: 20I l1+(20+50|+40)Il2+50I l 3=US1-US3 l 3: I l3=IS2=2A E3-7 The circuit is shown as Fig.E3-7, find the branch current using loop current analysis
电路学习指导 第三章电阻电路的一般分析 Solution The equations are 厂I11=5A 112=5U1 10w -2111+2112+(1+2+2I10 andU=2(111-11) 名 3058 50113=6A, 112=5U1=5×(-2F-10A The branch currents are 1=-1A12=1 ①4 1=5A1=113=6A 28 1=5U,=-10A1=112+113=-10+6=-4A o.5s Fig.E3-7 E3-8 The circuit is shown as Fig.E3-8,find the branch current using nodal voltage analysis Solution The nodal voltage equations are 下Ua 1:Ua1=10V 门R 2:-0.5Un1+0.5+0.5)Un2=-10-0.5×4 R 3:-0.2Ua1+0.2+0.2)Un=10-0.2×10 Solve them,we get Unl=10V Un2.=-7V Un3=25V The branch currents are I=(U1-Un3-10)×02=-5A Fig.E3-8 l2=(Ua1-U)x0.5=8.5A l=11+l=8.5-5=3.5A 11 I6=0.2Un3=5A E3-9 The circuit is shown as Fig.E3-9,write the nodal voltage equations. Solution
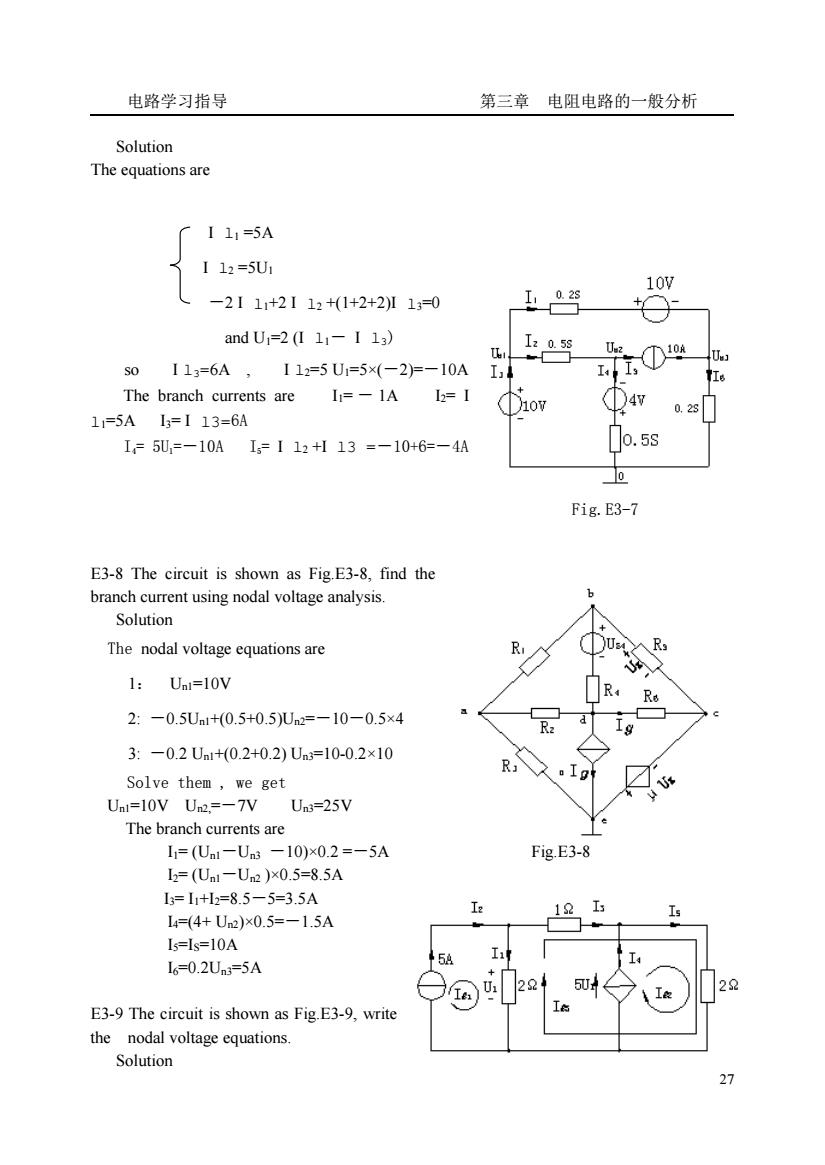
电路学习指导 第三章 电阻电路的一般分析 27 Solution The equations are I l1 =5A I l2 =5U1 -2 I l1+2 I l2 +(1+2+2)I l3=0 and U1=2 (I l1- I l3) so I l3=6A , I l2=5 U1=5×(-2)=-10A The branch currents are I1= - 1A I2= I l1=5A I3= I l3=6A I4= 5U1=-10A I5= I l2 +I l3 =-10+6=-4A Fig.E3-7 E3-8 The circuit is shown as Fig.E3-8, find the branch current using nodal voltage analysis. Solution The nodal voltage equations are 1: Un1=10V 2: -0.5Un1+(0.5+0.5)Un2=-10-0.5×4 3: -0.2 Un1+(0.2+0.2) Un3=10-0.2×10 Solve them , we get Un1=10V Un2,=-7V Un3=25V The branch currents are I1= (Un1-Un3 -10)×0.2 =-5A Fig.E3-8 I2= (Un1-Un2 )×0.5=8.5A I3= I1+I2=8.5-5=3.5A I4=(4+ Un2)×0.5=-1.5A I5=IS=10A I6=0.2Un3=5A E3-9 The circuit is shown as Fig.E3-9, write the nodal voltage equations. Solution