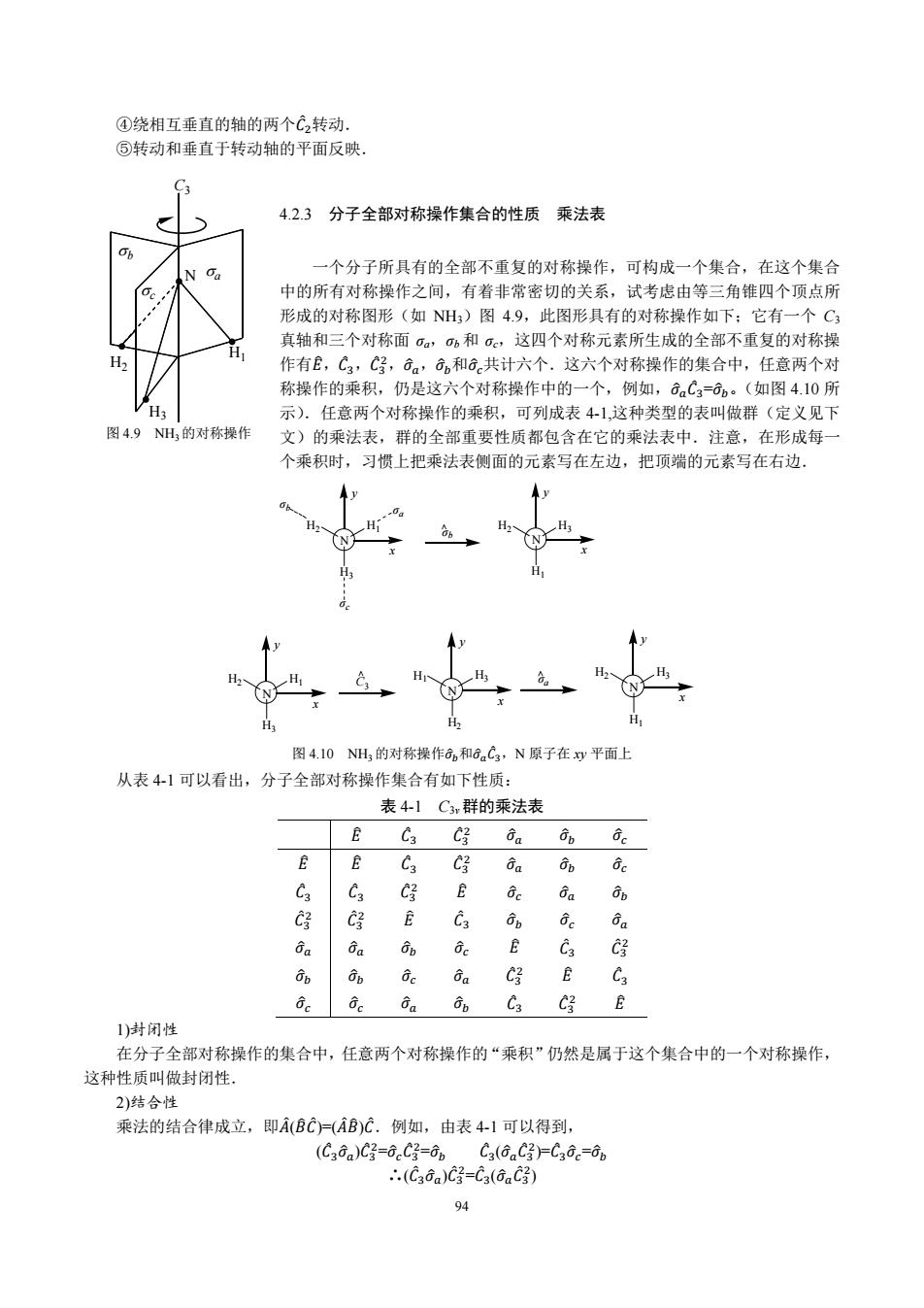
④绕相互垂直的轴的两个C2转动. ⑤转动和垂直于转动轴的平面反映。 C 4.2.3分子全部对称操作集合的性质乘法表 N Oa 一个分子所具有的全部不重复的对称操作,可构成一个集合,在这个集合 中的所有对称操作之间,有着非常密切的关系,试考虑由等三角锥四个顶点所 形成的对称图形(如NH3)图4.9,此图形具有的对称操作如下:它有一个C3 真轴和三个对称面oa,o6和,这四个对称元素所生成的全部不重复的对称操 H 作有E,C3,C好,6a,和6共计六个.这六个对称操作的集合中,任意两个对 称操作的乘积,仍是这六个对称操作中的一个,例如,6aC3=可。(如图4.10所 H3 示).任意两个对称操作的乘积,可列成表41,这种类型的表叫做群(定义见下 图4.9NH3的对称操作 文)的乘法表,群的全部重要性质都包含在它的乘法表中,注意,在形成每一 个乘积时,习惯上把乘法表侧面的元素写在左边,把顶端的元素写在右边. 0 H 图4.10NH3的对称操作和6aC3,N原子在xy平面上 从表4-1可以看出,分子全部对称操作集合有如下性质: 表4-1C3群的乘法表 E C3 c好 6 E C3 c好 a b C3 C3 C好 E c a Op C好 C好 C3 b Gc Ga 60 Ga 可b e E C3 c好 b Op Gc Ga C好 E C3 e Gc a Gp C3 c好 E 1)封闭性 在分子全部对称操作的集合中,任意两个对称操作的“乘积”仍然是属于这个集合中的一个对称操作, 这种性质叫做封闭性。 2)结合性 乘法的结合律成立,即A(BC)=(AB)C.例如,由表41可以得到, (C3aa)C好=6C好=6。C3(6aC3-C3e=b ∴.(C36a)C好=C3(⑥aC) 94
94 ④绕相互垂直的轴的两个ܥመ ଶ转动. ⑤转动和垂直于转动轴的平面反映. 4.2.3 分子全部对称操作集合的性质 乘法表 一个分子所具有的全部不重复的对称操作,可构成一个集合,在这个集合 中的所有对称操作之间,有着非常密切的关系,试考虑由等三角锥四个顶点所 形成的对称图形(如 NH3)图 4.9,此图形具有的对称操作如下;它有一个 C3 真轴和三个对称面 σa,σb 和 σc,这四个对称元素所生成的全部不重复的对称操 መܥ,ܧ作有 ଷ,ܥመ ଷ ଶ,ߪො,ߪො和ߪො共计六个.这六个对称操作的集合中,任意两个对 称操作的乘积,仍是这六个对称操作中的一个,例如,ߪොܥመ ଷ=ߪො。(如图 4.10 所 示).任意两个对称操作的乘积,可列成表 4-1,这种类型的表叫做群(定义见下 文)的乘法表,群的全部重要性质都包含在它的乘法表中.注意,在形成每一 个乘积时,习惯上把乘法表侧面的元素写在左边,把顶端的元素写在右边. N H1 H3 H2 σa σc x y σb N H3 H1 H2 x y σb < N H3 H1 H2 x y σa < N H3 H2 H1 x y < N H1 H3 H2 x y C3 图 4.10 NH3 的对称操作ߪො和ߪොܥመ ଷ,N 原子在 xy 平面上 从表 4-1 可以看出,分子全部对称操作集合有如下性质: 表 4-1 C3v群的乘法表 መܥ ܧ ଷ ܥመ ଷ ଶ ߪො ߪො ߪො ܧ መܥ ଷ መܥ ଷ ଶ ොߪ ොߪ ොߪ ܧ መܥ ଷ መܥ ଷ ଶ ොߪ ොߪ ොߪ መܥ ଷ መܥ ଷ ଶ ܧ ොߪ ොߪ ොߪ መܥ ଷ ଶ ܧ መܥ ଷ ොߪ ොߪ ොߪ ොߪ ොߪ ොߪ ܧ መܥ ଷ ଶ መܥ ଷ ොߪ ොߪ ොߪ መܥ ଷ ܧ መܥ ଷ ଶ ොߪ ොߪ ොߪ መܥ ଷ ଶ መܥ ଷ ܧ 1)封闭性 在分子全部对称操作的集合中,任意两个对称操作的“乘积”仍然是属于这个集合中的一个对称操作, 这种性质叫做封闭性. 2)结合性 乘法的结合律成立,即ܣመ(ܤܥመ)=(ܣመܤ(ܥመ.例如,由表 4-1 可以得到, መܥ) ଷߪො)ܥመ ଷ ଶ=ߪොܥመ ଷ ଶ=ߪො ܥመ ଷ(ߪොܥመ ଷ ଶ)=ܥመ ଷߪො=ߪො መܥ)∴ ଷߪො)ܥመ ଷ ଶ=ܥመ ଷ(ߪොܥመ ଷ ଶ) 图 4.9 NH3的对称操作 a c b C3 N H1 H2 H3

3)恒等元 集合中含有一个恒等操作E,它同集合中的任一对称操作A的乘积都有AE=EA=A,即任一对称操作乘以 恒等元保持不变。 4)逆元 集合中每一个对称操作A一定有一个逆元A-1,也是集合中的一个对称操作,使得AA-1=A-1A=E,例如 C3c好=E,则C31=好。 由于分子全部对称操作的集合满足如上四条性质,构成一个对称群. 4.3群的基本概念 我们要用对称性讨论分子的电子结构以及分子的振动和转动,就要用到称为群论的数学分支,群论是 在18世纪的后期开始发展起来的,数学家伽略华(Evaristte Galois)(1832年.死于决斗,年仅二十一岁)和 阿贝尔Niels Abel)(I829年.死于肺结核,年方二十六岁)对群论的发展作了重大的贡献,凯雷(Arthur Cayley) 对群给了完整的定义, 4.3.1群的定义 群的概念是抽象的,考虑元素A,B,C,…的一个集合,其中任何两个元素都不相同.这些元素可以 是数,但并不需要它们一定是数,假设我们定义一个结合规则(称为“乘法”)用符号*表示,则任意两个 元素A和B按给定次序的“乘积”唯一地被确定,例如用P表示此乘积,A*B=P(按相反顺序的“乘积” B*A不一定等于A*B).在此讲的“结合规则”不一定是算术中的乘法,它可以是任何经适当定义的规则.A, B,C,…等元素的集合,满足以下四个条件时就称这个集合在指定的结合规则下形成一个群: 1)封闭性 如A和B是群的任意两个元素,则它们的积A*B也一定是该群的元素, 2)结合性 结合规则(“乘法”)一定要满足结合律:如果A,B和C是群的任意三个元素,则(A*B)*C=A*(B*C). 3)恒等元 群必须含有一个单独的元素E,对于群中的任何元素A,都有A*E=E*A=A.我们称E为恒等元.群的元 素乘以恒等元保持不变. 4)逆元 群的每一个元素A一定有一个逆元素,它也是该群的一个元素.术语避元意味着A*A='*A=E,E 是恒等元。 只要提到元素A,B,C,…的集合形成一个群,总是假定所有的群元素都不相同,群中元素的数目叫 做群的阶.因封闭性的要求,当我们考虑A和B相乘时,不能排除A和B是相同元素的可能性,即要求A*A 仍为群的一个元素.注意群的元素不按特定的次序排列, 4.3.2群的几个例子 让我们看几个例子,考虑从1到10的整数集合,并设结合规则是加法,我们能否得到一个群呢?回答 是不能.因为它不满足封闭性.例如8+7=15,而15不是元素1,2,…10集合的成员. 再考虑所有正整数1,2,3,…的集合,结合规则是普通的乘法.封闭性是满足的,因为任意两个正整 数的乘积仍为一个正整数.一般乘法是可以结合的,所以满足结合性条件.(不要认为结合性是理所当然的, 它并不是在任何情况下都是正确的.指数就不能结合运算,如(2)2=64,而23)=512)恒等元是1,因而满足条 95
95 3)恒等元 即任一对称操作乘以,መܣ=መܣܧ=ܧመܣመ的乘积都有ܣ它同集合中的任一对称操作,ܧ集合中含有一个恒等操作 恒等元保持不变。 4)逆元 集合中每一个对称操作ܣመ一定有一个逆元ܣመିଵ,也是集合中的一个对称操作,使得ܣመܣመିଵ=ܣመିଵܣመ=ܧ,例如 መܥ ଷܥመ ଷ ଶ =ܧ,则ܥመ ଷ ିଵ=ܥመ ଷ ଶ。 由于分子全部对称操作的集合满足如上四条性质,构成一个对称群. 4.3 群的基本概念 我们要用对称性讨论分子的电子结构以及分子的振动和转动,就要用到称为群论的数学分支,群论是 在 18 世纪的后期开始发展起来的,数学家伽略华(Evaristte Galois)(1832 年.死于决斗,年仅二十一岁)和 阿贝尔(Niels Abel) (1829 年.死于肺结核,年方二十六岁)对群论的发展作了重大的贡献,凯雷(Arthur Cayley) 对群给了完整的定义. 4.3.1 群的定义 群的概念是抽象的,考虑元素 A,B,C,…的一个集合,其中任何两个元素都不相同.这些元素可以 是数,但并不需要它们一定是数,假设我们定义一个结合规则(称为“乘法”)用符号*表示,则任意两个 元素 A 和 B 按给定次序的“乘积”唯一地被确定.例如用 P 表示此乘积,A*B=P(按相反顺序的“乘积” B*A 不一定等于 A*B).在此讲的“结合规则”不一定是算术中的乘法,它可以是任何经适当定义的规则.A, B,C,…等元素的集合,满足以下四个条件时就称这个集合在指定的结合规则下形成一个群: 1)封闭性 如 A 和 B 是群的任意两个元素,则它们的积 A*B 也一定是该群的元素. 2)结合性 结合规则(“乘法”)一定要满足结合律:如果 A,B 和 C 是群的任意三个元素,则(A*B)*C=A*(B*C). 3)恒等元 群必须含有一个单独的元素 E,对于群中的任何元素 A,都有 A*E=E*A=A.我们称 E 为恒等元.群的元 素乘以恒等元保持不变. 4)逆元 群的每一个元素 A 一定有一个逆元素 A-1,它也是该群的一个元素.术语避元意味着 A*A-1=A-1*A =E,E 是恒等元。 只要提到元素 A,B,C,…的集合形成一个群,总是假定所有的群元素都不相同,群中元素的数目叫 做群的阶.因封闭性的要求,当我们考虑 A 和 B 相乘时,不能排除 A 和 B 是相同元素的可能性,即要求 A*A 仍为群的一个元素.注意群的元素不按特定的次序排列. 4.3.2 群的几个例子 让我们看几个例子,考虑从 1 到 10 的整数集合,并设结合规则是加法,我们能否得到一个群呢?回答 是不能.因为它不满足封闭性.例如 8+7=15,而 15 不是元素 1,2,…10 集合的成员. 再考虑所有正整数 1,2,3,…的集合,结合规则是普通的乘法.封闭性是满足的,因为任意两个正整 数的乘积仍为一个正整数.一般乘法是可以结合的,所以满足结合性条件.(不要认为结合性是理所当然的, 它并不是在任何情况下都是正确的.指数就不能结合运算,如(23 ) 2 =64,而2ሺଷమሻ =512)恒等元是 1,因而满足条

件(3).可是集合中只有1有逆元素(1的逆元素还是1),所以不满足条件(4),不能够构成一个群。 下面考虑零以外的全部实数集合,结合规则是普通乘法,两个非零实数的乘积仍是一个实数,因此满 足封闭性.满足结合性.恒等元是1,最后,每个元素都有一个逆元,即该数的倒数,所以全部非零实数的 集合在一般乘法的结合规则下形成一个群,该群的阶是无穷大.(如果零包括在集合中,就不能够成一个群, 因为零没有逆元.) 全部正、负整数及零的集合是一个群.在这里结合规则不是算术乘法,而是一般加法.封闭性是满足 的,加法是可以结合的,恒等元是零:A+0=A=0+A.每个元素的逆元是它的负数:A+(-A)=A+(-A)=0 从上节的讨论可知,分子的全部对称操作的集合,满足群定义的四个条件,构成一个群. 4.3.3子群,类和群的同构 群论的威力来自它的抽象性,无须对群元素的性质或结合规则作具体规定,只需群定义的四个条件, 群的数学定理都可以证明.群的本质不在于构成群的元素是什么,而在于它们必须服从上述的四项运算规 则.这些运算规则反映了群中各元素之间的内在联系 若一个群的子集合按照与原来群相同的结合规则(乘法)构成一个群,则称元素的子集合形成原来群 的子群,例如,NH3分子全部对称操作构成的对称群是一个6阶群,它的乘法表由表4-1给出,在这个6阶 群中,可以验证,(E,C3,C)三个对称操作所构成的集合,也是一个群,这个群的阶数是3,因此,它是 上述6阶群的一个子群.除此之外,在这个6阶群中,还包含有三个二阶子群,它们分别由二个对称操作(E, a),(E,b),(E,c)所构成. 如果同一个群中的元素P和Q满足关系P=XQX,其中X也是此群的元素(X不必与P或Q不同),则 我们称P和Q共轭.注意若P=XQX,则左乘以X接着右乘以X,就得到:Q=XPX:X也是该群的某个元 素,把它叫做Y,即Q=YPY.因此,若P与Q共轭,则Q亦跟P共轭,而且,容易证明:若P跟Q共轭, R也跟Q共轭,则P和R互为共轭。从而我们可以把一个群的元素分为若干个由彼此共轭的元素组成的子 集合,称每一个这样的子集合为类。 作为一个例子,我们寻找C群NH,分子全部对称操作的集合)的类.为了找出与E属于同一类的元素, 我们要写出所有可能的形如XEX的乘积,因为XEX=EXX=E,所以元素E自成一类,再看a,利用群的 乘法表4-1,可以求出 E-10aE=0a:C310aC3=Gc:(C3)GaC3=0p:GaGaGa-6a:0b0aOp-0c:6c0a0c=6b 因此a,和形成C3r群的一个类.(为了进行检验,我们可以写出如8-18,或8-1的所有乘积.) 最后, E-1C3E=C3:C31C3C3=C3:(C好)C3C好=C3:6a1C3aa=C好;661C3=C3;6e1C36e=C3 所以,C3和C好形成一类.C3m有三个类.①E:②6a,b,6c:③C3,C好 注意,每一类的成员是密切相关的对称操作. 如果所有的群元素全都对易(即AB=BA),这样的群叫做阿贝尔群(Abelian)或交换群.交换群的一个特 例是循环群.例如C3群(E=C3,C3,C好=C经)就是一个循环群,对于阿贝尔群,每个元素都自成一类,因为 Y'AY=AYY=A. 因为反演与任何别的对称操作对易,故具有对称中心的分子点群其自成一类, 最后来介绍群的同构概念.两个同阶的群A(a,',a”,…)和B(b,b',b”,…),如果在双方的元素间可以建立 起某种一一对应关系,使得元素a对应于元素b以及元素a对应于元素b时,就有元素a=aa对应于元素 b”=bb',则这两个群就称为同构的.这样的两个群从抽象观点看来显然具有相同的性质,尽管它们的元素具 有不同的实际含义, 96
96 件(3).可是集合中只有 1 有逆元素(1 的逆元素还是 1),所以不满足条件(4),不能够构成一个群. 下面考虑零以外的全部实数集合,结合规则是普通乘法,两个非零实数的乘积仍是一个实数,因此满 足封闭性.满足结合性.恒等元是 1.最后,每个元素都有一个逆元,即该数的倒数,所以全部非零实数的 集合在一般乘法的结合规则下形成一个群,该群的阶是无穷大.(如果零包括在集合中,就不能够成一个群, 因为零没有逆元.) 全部正、负整数及零的集合是一个群.在这里结合规则不是算术乘法,而是一般加法.封闭性是满足 的,加法是可以结合的,恒等元是零:A+0=A=0+A.每个元素的逆元是它的负数:A+(െA)=A+(െA)=0 从上节的讨论可知,分子的全部对称操作的集合,满足群定义的四个条件,构成一个群. 4.3.3 子群,类和群的同构 群论的威力来自它的抽象性,无须对群元素的性质或结合规则作具体规定,只需群定义的四个条件, 群的数学定理都可以证明.群的本质不在于构成群的元素是什么,而在于它们必须服从上述的四项运算规 则.这些运算规则反映了群中各元素之间的内在联系. 若一个群的子集合按照与原来群相同的结合规则(乘法)构成一个群,则称元素的子集合形成原来群 的子群,例如,NH3 分子全部对称操作构成的对称群是一个 6 阶群,它的乘法表由表 4-1 给出,在这个 6 阶 群中,可以验证,由(ܧ ,ܥመ ଷ, ܥመ ଷ ଶ)三个对称操作所构成的集合,也是一个群,这个群的阶数是 3,因此,它是 上述 6 阶群的一个子群.除此之外,在这个 6 阶群中,还包含有三个二阶子群,它们分别由二个对称操作(ܧ , .所构成)ොߪ ,ܧ),(ොߪ ,ܧ),(ොߪ 如果同一个群中的元素 P 和 Q 满足关系 P=X-1QX,其中 X 也是此群的元素(X 不必与 P 或 Q 不同),则 我们称 P 和 Q 共轭.注意若 P=X-1QX,则左乘以 X,接着右乘以 X-1,就得到;Q=XPX-1 ;X-1 也是该群的某个元 素,把它叫做 Y,即 Q=Y-1PY.因此,若 P 与 Q 共轭,则 Q 亦跟 P 共轭,而且,容易证明:若 P 跟 Q 共轭, R 也跟 Q 共轭,则 P 和 R 互为共轭。从而我们可以把一个群的元素分为若干个由彼此共轭的元素组成的子 集合,称每一个这样的子集合为类。 作为一个例子,我们寻找 C3v群(NH3 分子全部对称操作的集合)的类.为了找出与ܧ属于同一类的元素, 我们要写出所有可能的形如 X-1ܧX 的乘积,因为 X-1ܧX=ܧX-1X=ܧ,所以元素ܧ自成一类,再看ߪො,利用群的 乘法表 4-1,可以求出 መܥ;ොߪ=ܧොߪଵିܧ ଷ ିଵߪොܥመ ଷ=ߪො;(ܥመ ଷ ଶ) -1 መܥොߪ ଷ ଶ=ߪො;ߪො ିଵߪොߪො=ߪො;ߪො ିଵߪොߪො=ߪො;ߪො ିଵߪොߪො=ߪො 因此ߪො,ߪො和ߪො形成 C3v 群的一个类.(为了进行检验,我们可以写出如ܺିଵߪොܺ,或ܺିଵߪොܺ的所有乘积.) 最后, መܥଵିܧ መܥ=ܧଷ ଷ;ܥመ ଷ ିଵܥመ ଷܥመ ଷ=ܥመ ଷ;(ܥመ ଷ ଶ) -1ܥመ ଷܥመ ଷ ଶ=ܥመ ଷ;ߪො ିଵܥመ ଷߪො=ܥመ ଷ ଶ ොߪ; ିଵܥመ ଷߪො=ܥመ ଷ ଶ ොߪ; ିଵܥመ ଷߪො=ܥመ ଷ ଶ 所以, ܥመ ଷ和ܥመ ଷ ଶ形成一类.C3v有三个类.①ܧ2;ߪො,ߪො,ߪො;③ܥመ ଷ,ܥመ ଷ ଶ 注意,每一类的成员是密切相关的对称操作. 如果所有的群元素全都对易(即 AB= BA),这样的群叫做阿贝尔群(Abelian)或交换群.交换群的一个特 例是循环群.例如 C3 群(ܧ=ܥመ ଷ ଷ,ܥመ ଷ,ܥመ ଷ ଶ=ܥመ ଷ ଶ)就是一个循环群,对于阿贝尔群,每个元素都自成一类,因为 X-1AX =AX-1X =A. 因为反演与任何别的对称操作对易,故具有对称中心的分子点群其ଓ自成一类. ̂ 最后来介绍群的同构概念.两个同阶的群 A(a, a', a'',…)和 B(b, b', b'',…),如果在双方的元素间可以建立 起某种一一对应关系,使得元素 a 对应于元素 b 以及元素 a'对应于元素 b'时,就有元素 a''=aa'对应于元素 b''=bb',则这两个群就称为同构的.这样的两个群从抽象观点看来显然具有相同的性质,尽管它们的元素具 有不同的实际含义.

4.4对称点群 一个分子的全部对称操作的集合形成一个数学群.对于分子的任一个对称操作,质量中心是保持固定 的,于是一个孤立分子的对称群叫做点群.对于无限伸展的晶体,可以有对称操作(例如,平移)使得没 有一个点是固定不动的,这给出空间群.我们略去空间群的讨论。 4.4.1对称点群 任一分子可归为我们所列举的对称点群之一,为方便计,我们将点群分为四部分, 1)无Cn轴的群:C1,Ca,C (1)C如果一个分子全无对称元素,它属于此群,仅有 的对称操作是E(是一个C转动).CHFCIBr属于点群C. (2)C。一个分子其仅有的对称元素是一个对称面者属 于此群.对称操作是E和6.一个例子是HOC1(图4.11). Co C (3)C:一个分子其仅有的对称元素是对称中心者属于此 图4.11无Cn轴的分子 群.对称操作是E和1.一个例子见图4.11. 2)有一个Cn轴的群:Cn,Ch,Cm,S2 (1)Cm,n=2,3,4…一个分子仅有的对称元素是一个Cn轴者属于此群,对称操作是Cn,C经,…,E, 属于C2分子的例子示于图4.12. (2)CM,=2,3,4,·如果垂直于Cn轴增加一个对称面,则分子属子这种群.因为nCm=Sn,所以 Cn轴也是Sn轴.若n为偶数,Cn轴也是C2轴而有对称操作 GnC2=S2=i 于是对于偶数n,属于Ch的分子有对称中心.(Ch群是前面己讨论过的C1群.)属于C2h和C3群的分子 的例子示于图4.12. (3)Cm,=2,3,4,·属于这种群的分子有一个Cn轴和n个竖直对称面(通过Cn轴).H0分子有 一个C2轴和二个竖直对称面,属于C2.NH分子属于C3(见图4.12) C2 C H2O2(O-0键垂直于纸面) 图4.12只有一个Cn轴的分子 (4)Sn,n=4,6,8,…Sn是联系着Sn轴的对称操作群,先考虑n为奇数的情 况.我们有Sn=6nCm·操作Cn只影响x和y坐标:而操作G只影响z坐标,于是这 些操作可以对易,而有 Sn=(OnCn)"=OnCnOnCnOnCn-On Cn 现在C=E,且对于奇数n,6=.于是对于奇数n,S?等于6h,而群S.有一水 平对称平面.以及 S+1=SSn=nSn=hnCm=Cn,n为奇数 所以n为奇数时有一Cn轴.我们断定,若n为奇数,Sn群等于Ch群。 现在考虑n为偶数.目为S2=1,群S2等于C,于是只有=4,6,8,…时才得到 图4.13 97
97 图 4.13 4.4 对称点群 一个分子的全部对称操作的集合形成一个数学群.对于分子的任一个对称操作,质量中心是保持固定 的,于是一个孤立分子的对称群叫做点群.对于无限伸展的晶体,可以有对称操作(例如,平移)使得没 有一个点是固定不动的,这给出空间群.我们略去空间群的讨论。 4.4.1 对称点群 任一分子可归为我们所列举的对称点群之一.为方便计,我们将点群分为四部分. 1)无 Cn轴的群:C1,Cσ,Ci (1)C1 如果一个分子全无对称元素,它属于此群,仅有 的对称操作是ܧ)是一个ܥመ ଵ转动).CHFClBr 属于点群 C1. (2)Cσ 一个分子其仅有的对称元素是一个对称面者属 于此群.对称操作是ܧ和ߪො.一个例子是 HOCl(图 4.11). (3)Ci 一个分子其仅有的对称元素是对称中心者属于此 群.对称操作是ܧ和ଓ.一个例子见图 ̂ 4.11. 2)有一个 Cn轴的群:Cn,Cnh,Cnv,S2n (1)Cn,n=2,3,4… 一个分子仅有的对称元素是一个 Cn 轴者属于此群,对称操作是ܥመ መܥ, ,ܧ,...,ଶ 属于 C2 分子的例子示于图 4.12. (2)Cnh,n=2,3,4,… 如果垂直于 Cn 轴增加一个对称面,则分子属子这种群.因为ߪොܥመ =ܵመ ,所以 Cn 轴也是 Sn轴.若 n 为偶数,Cn 轴也是 C2 轴而有对称操作 መܥොߪ ଶ=ܵመ ଶ=ଓ̂ 于是对于偶数 n,属于 Cnh 的分子有对称中心.(C1h 群是前面已讨论过的 C1 群.)属于 C2h 和 C3h 群的分子 的例子示于图 4.12. (3)Cnv,n=2,3,4,… 属于这种群的分子有一个 Cn 轴和 n 个竖直对称面(通过 Cn轴).H2O 分子有 一个 C2 轴和二个竖直对称面,属于 C2v.NH3 分子属于 C3v(见图 4.12). H H C2 C2 H H H F H F C C F H H F B O O O H H H N H H H C3 C2 C2 C2h C3h C3v H2O2(O-O 键垂直于纸面) 图 4.12 只有一个 Cn轴的分子 (4)Sn,n=4,6,8,… Sn是联系着 Sn轴的对称操作群,先考虑 n 为奇数的情 况.我们有ܵመ መܥොߪ= .操作ܥመ 只影响 x 和 y 坐标;而操作ߪො只影响 z 坐标,于是这 些操作可以对易,而有 ܵመ መܥොߪ)= ) n መܥොߪ= መܥොߪ መܥොߪ... ොߪ= መܥ 现在ܥመ =ܧ,且对于奇数 n,ߪො =ߪො.于是对于奇数 n,ܵመ 等于ߪො,而群 Sn 有一水 平对称平面.以及 ܵመ ାଵ=ܵመ ܵመ =ߪොܵመ መܥොߪොߪ= መܥ= ,n 为奇数 所以 n 为奇数时有一 Cn轴.我们断定,若 n 为奇数,Sn 群等于 Cnh 群. 现在考虑 n 为偶数.目为ܵመ ଶ=ଓ,群̂ S2 等于 Ci,于是只有 n=4, 6, 8, …时才得到 C1 Cσ Ci 图 4.11 无 Cn 轴的分子 C Cl F Br H O H Cl Cl F H Cl H H H F H F H F H F S4

新的群.S2m轴也是一个Cn轴: S经n=好C径n=ECn=Cn 图4.13中螺旋体属于S4群. 3)有一个Cn轴和n个C2轴的群:Dnm,Dh,Dnd (1)Dn,=2,3,4,…一个分子有一个Cn轴和n个垂直于Cn轴的 C2轴(而无对称面)者属于Dn群,相邻的C,轴的夹角是严弧度,对 n 于D2群,有三个互相垂直的C2轴,对称操作是E,C2(x,C20y),C2(e), (2)Dh,=2,3,4,…属于这种群的分子有一Cn轴,n个C2轴,以及 一个垂直于Cn轴的o%对称面,如同C中那样,Cn轴也是Sn轴.若n 为偶数,Cn轴是一个C2轴也是一个S2轴,所以有一个对称中心.D 分子中还有n个竖直的对称面,每个这样的面通过Cn轴和一个C2轴, 我们现在证明这个论断.建立一个坐标系使Cn轴为:轴,令C2轴之 C2 x 一为x轴(图4.14).这使得y平面是0.对称面.观察乘积(y)C2(x) 图4.14在D.分子中的二个对称轴 对于一个原来在(x,y,)的点的效果.有因为(y)C2(x)与(xa)两者均 将原来在(x,y,)的点移到最后的位置(x,一y,),它们是相等的: (xy)C2(x)=6(x=) C2(x)和(y)是对称操作,它们的乘积必定是对称操作:所以,:平面是一个对称面.同样的论证适于任意 C2轴,所以有们个o面.BF3属于D3h:PtC142属于D4h,苯属于D6a(图4.15) K,y)C化-y-)yk,-y也有化,))x-y) C B Dah D6h Did 图4.15有一个Cn轴和n个C2轴的分子 因为(y)C2(x)与(x)两者均将原来在(x,y,)的点移到最后的位置(x,-y,),它们是相等的: 6(xy)C2(x)=6(x=) C2(x)和()是对称操作,它们的乘积必定是对称操作:所以,:平面是一个对称面.同样的论证适于任意 C2轴,所以有们个o面.BF3属于D3h:PtCI属于D4h,苯属于D6(图4.15). (3)Dd,=2,3,4,…分子有一个Cn轴,n个C2轴和n个竖直的对称面通过Cn轴并平分两相邻的C2 轴的夹角,属于这种群,n个竖直的平面叫做等分面,以符号o表之.可以证明,Cn轴是一个S2n轴.乙烷 的参差式构象是D3群的一例(图4.15).[有内旋转的分子的对称性(例如,乙烷)实际上需要特别的讨论, 我们略去.] 4)有多于一个Cn轴(n>2)的群:TaT,Th,O,Oh,h,I,Kh 这些群与柏拉图体的对称性有关,柏拉图体被全等的正多边形所包围并有全等多面角.有五种这样的 柏拉图体:有四个三角形的四面体,有六个四方形的立方体,有八个三角形的八面体,有十二个五边形的 五边形十二面体,有二十个三角形的二十面体.(五边形十二面体勿与三角形十二面体相混淆:后者有十二 个三角面但不是一个柏拉图体.) (I)T:一个正四面体的对称操作组成此群.最好的例子是CH4.CH4的对称元素是四个C3轴(每个CH 键),三个S4轴它们也是C2轴(图4.16),六个对称面,每个这样的面包含两个C-H键.(四件事每次取两 件的组合数为41/2121=6). 98
98 新的群.S2n轴也是一个 Cn 轴: ܵመ ଶ ଶ =ߪො ଶܥመ ଶ መܥܧ= ଶ መܥ= 图 4.13 中螺旋体属于 S4群. 3)有一个 Cn轴和 n 个 C2轴的群:Dn, Dnh, Dnd (1)Dn,n=2, 3, 4, … 一个分子有一个 Cn 轴和 n 个垂直于 Cn 轴的 C2 轴(而无对称面)者属于 Dn 群,相邻的 C2 轴的夹角是గ 弧度,对 于 D2 群,有三个互相垂直的 C2 轴,对称操作是 ܧ ,ܥመ ଶ(x), ܥመ ଶ(y), ܥመ ଶ(z). (2)Dnh,n=2, 3, 4, … 属于这种群的分子有一 Cn轴,n 个 C2轴,以及 一个垂直于 Cn 轴的 σh 对称面,如同 Cnh 中那样,Cn 轴也是 Sn 轴.若 n 为偶数,Cn 轴是一个 C2 轴也是一个 S2 轴,所以有一个对称中心.Dnh 分子中还有 n 个竖直的对称面,每个这样的面通过 Cn 轴和一个 C2 轴, 我们现在证明这个论断.建立一个坐标系使 Cn 轴为 z 轴,令 C2 轴之 一为 x 轴(图 4.14).这使得 xy 平面是 σh 对称面.观察乘积ߪො(xy)ܥመ ଶ(x) 对于一个原来在(x,y,z)的点的效果.有因为ߪො(xy)ܥመ ଶ(x)与ߪො(xz)两者均 将原来在(x, y, z)的点移到最后的位置(x, െy, z),它们是相等的: ߪො(xy)ܥመ ଶ(x)=ߪො(xz) መܥ ଶ(x)和ߪො(xy)是对称操作,它们的乘积必定是对称操作;所以,z 平面是一个对称面.同样的论证适于任意 C2 轴,所以有们个 σy面.BF3 属于 D3h;PtCl4 2-属于 D4h,苯属于 D6h(图 4.15). (x, y, z) → (x, െy, െz) → (x, െy, z) 也有 (x, y, z) → (x, െy, z) B F F F Pt Cl Cl Cl Cl 2- H H H H H H σd C2 D3h D4h D6h D3d 图 4.15 有一个 Cn 轴和 n 个 C2 轴的分子 因为ߪො(xy)ܥመ ଶ(x)与ߪො(xz)两者均将原来在(x, y, z)的点移到最后的位置(x, െy, z),它们是相等的: ߪො(xy)ܥመ ଶ(x)=ߪො(xz) መܥ ଶ(x)和ߪො(xy)是对称操作,它们的乘积必定是对称操作;所以,z 平面是一个对称面.同样的论证适于任意 C2 轴,所以有们个 σy面.BF3 属于 D3h;PtClସ ଶି属于 D4h,苯属于 D6h(图 4.15). (3)Dnd,n=2, 3, 4, … 分子有一个 Cn轴,n 个 C2轴和 n 个竖直的对称面通过 Cn 轴并平分两相邻的 C2 轴的夹角,属于这种群,n 个竖直的平面叫做等分面,以符号 σd 表之.可以证明,Cn 轴是一个 S2n 轴.乙烷 的参差式构象是 D3d 群的一例(图 4.15 ).[有内旋转的分子的对称性(例如,乙烷)实际上需要特别的讨论, 我们略去.] 4)有多于一个 Cn轴(n>2)的群:Td,T,Th,O,Oh,Ih,I,Kh 这些群与柏拉图体的对称性有关,柏拉图体被全等的正多边形所包围并有全等多面角.有五种这样的 柏拉图体:有四个三角形的四面体,有六个四方形的立方体,有八个三角形的八面体,有十二个五边形的 五边形十二面体,有二十个三角形的二十面体.(五边形十二面体勿与三角形十二面体相混淆:后者有十二 个三角面但不是一个柏拉图体.) (1)Td 一个正四面体的对称操作组成此群.最好的例子是 CH4.CH4 的对称元素是四个 C3 轴(每个 C-H 键),三个 S4轴它们也是 C2 轴(图 4.16),六个对称面,每个这样的面包含两个 CെH 键.(四件事每次取两 件的组合数为 4!/2!2!=6). 图 4.14 在 Dnh 分子中的二个对称轴 መܥ ଶ(x) ߪො(xy) ߪො(xz) x y z Cn C2