
2.3 线型缩聚动力学 1.官能团等活性理论 缩聚反应在形成大分子的过程中是逐步进行的 若每一步都有不同的速率常数,研究将无法进行 原先认为,官能团的活性将随分子量增加而递减 Flory提出了官能团等活性理论: 不同链长的端基官能团,具有相同的反应能力和参加 反应的机会,即官能团的活性与分子的大小无关 Floy对此进行了解锋 同时指出,官能团等活性理论是近似的,不是绝对的 这一理论大大简化了研究处理,可用同一平衡常数表示 整个缩聚过程可以用两种官能团之间的反应来表征 COOH+HO∞ 2024/10/7 k-1 16
2024/10/7 16 2.3 线型缩聚动力学 缩聚反应在形成大分子的过程中是逐步进行的 若每一步都有不同的速率常数,研究将无法进行 原先认为,官能团的活性将随分子量增加而递减 Flory提出了官能团等活性理论: 不同链长的端基官能团,具有相同的反应能力和参加 反应的机会,即官能团的活性与分子的大小无关 Flory对此进行了解释 同时指出,官能团等活性理论是近似的,不是绝对的 这一理论大大简化了研究处理,可用同一平衡常数表示 整个缩聚过程可以用两种官能团之间的反应来表征 1. 官能团等活性理论 COOH + HO k1 k 1 OCO

2.线型缩聚动力学 口不可逆条件下的缩聚动力学 在不断排出低分子副产物时符合不可逆条件 以聚酯化反应为例,聚酯是酸催化反应 O OH C-OH HA k1_ C-OH A K2 OH 慢 OH C-OH HO K4 OH C-O+HO +H 2024/10/7
2024/10/7 17 2. 线型缩聚动力学 不可逆条件下的缩聚动力学 在不断排出低分子副产物时符合不可逆条件 以聚酯化反应为例,聚酯是酸催化反应 C OH + HA k1 O C OH OH k2 + + A - C OH OH + + HO k3 k4 C OH OH + OH k5 C O O + H2 O + H + 慢

k是最慢的一步反应,由于不可逆,k暂不考虑 聚酯反应速率用羧基消失速率来表示: Rp= dIcooH 1=ka[C"(OH)O ① dt [C+(OHD2]是质子化羧基的浓度,难以确定,设法消去 K,= k,_[C(OH2][A] k2 [COOH JIHA] [C*1OH2]= ki[COOH IHA k2IΓ1 代入①式 2024/10/7 18
2024/10/7 18 k3是最慢的一步反应,由于不可逆,k4暂不考虑 聚酯反应速率用羧基消失速率来表示: [C+ (OH)2 ]是质子化羧基的浓度,难以确定,设法消去 k [C (OH ) ] [OH ] dt d [COOH ] Rp 3 2 + =- = [COOH ] [ HA] [C (OH ) ] [ A ] k k K 2 2 1 + = = - , + = k [ A ] k [COOH ] [ HA] [C (OH ) ] 2 1 2 - 代入式
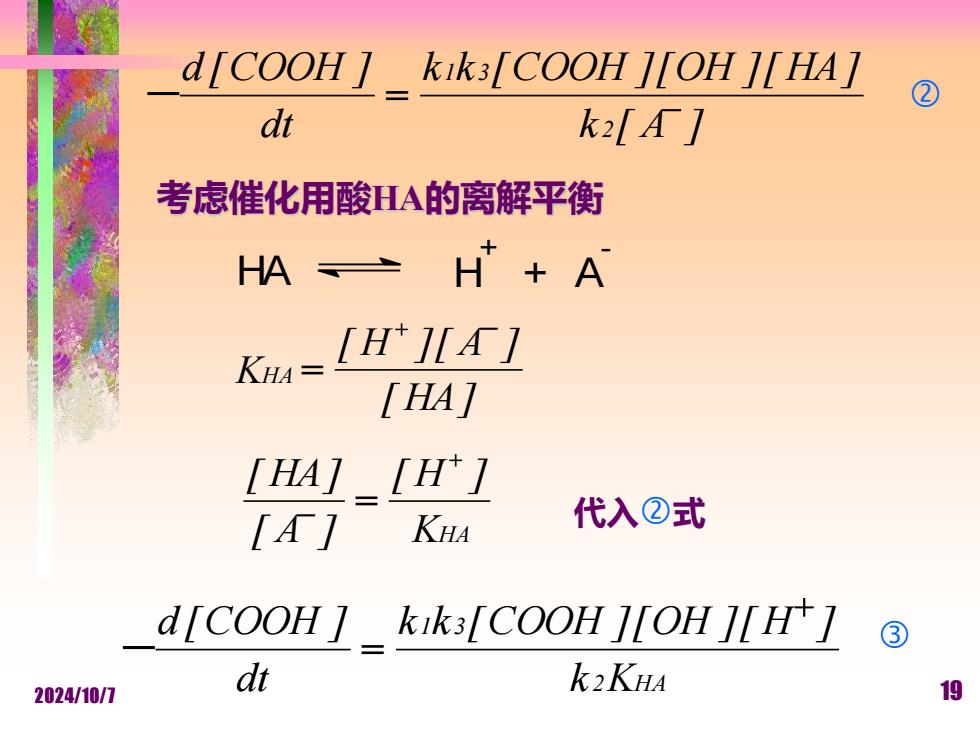
d[COOH 1 kik3[COOH J[OH ]IHA] ② dt k2[Γ1 考虑催化用酸HA的离解平衡 HA≥ H+A KH= [H]I1 [HA [HA] [H1 [] KHA 代入②式 d[COOH kik3[COOH J[OH [H1 ③ 2024/10/7 dt k2KHA 19
2024/10/7 19 考虑催化用酸HA的离解平衡 k [ A ] k k [COOH ] [OH ] [ HA] dt d [COOH ] 2 1 3 - = - HA H + + A - [ HA] [ H ] [ A ] KHA + - = KHA [ H ] [ A ] [ HA] + - = 代入式 2 HA 1 3 k K k k [COOH ] [OH ] [ H ] dt d [COOH ] + - =

催化用酸HA:可以是二元酸本身,但反应较慢 也可以是外加酸,如H2S04,大大加速 自催化缩聚反应 无外加酸,二元酸单体作催化剂,HA]=[COOH田 羧基与羟基浓度相等,以C表示,将②式中的所有 常数及[A]合并成k dC =kC3 表明自催化的聚酯 dt 反应呈三级反应 积分 1 C2 ci 2kt W 由反应程度P=1 No 羧基数用羧基浓度C代替 2024/10/7 20
2024/10/7 20 催化用酸HA:可以是二元酸本身,但反应较慢 也可以是外加酸,如H2SO4,大大加速 自催化缩聚反应 无外加酸,二元酸单体作催化剂,[HA] = [COOH] 羧基与羟基浓度相等,以C表示,将式中的所有 常数及[A-]合并成 k 表明自催化的聚酯 反应呈三级反应 3 kC dt dC - = 积分 2kt C 1 C 1 2 0 2 - = 由反应程度 N0 N P = 1- 羧基数用羧基浓度C代替