西安毛子科技大学洛必达法则XIDIAN UNIVERSITYx-sin x例1 求极限 limx→00解这是未定式由洛必达法则得011-cosxsinxsin xx-lim= lim lim33x266xx->0x->0x-00000
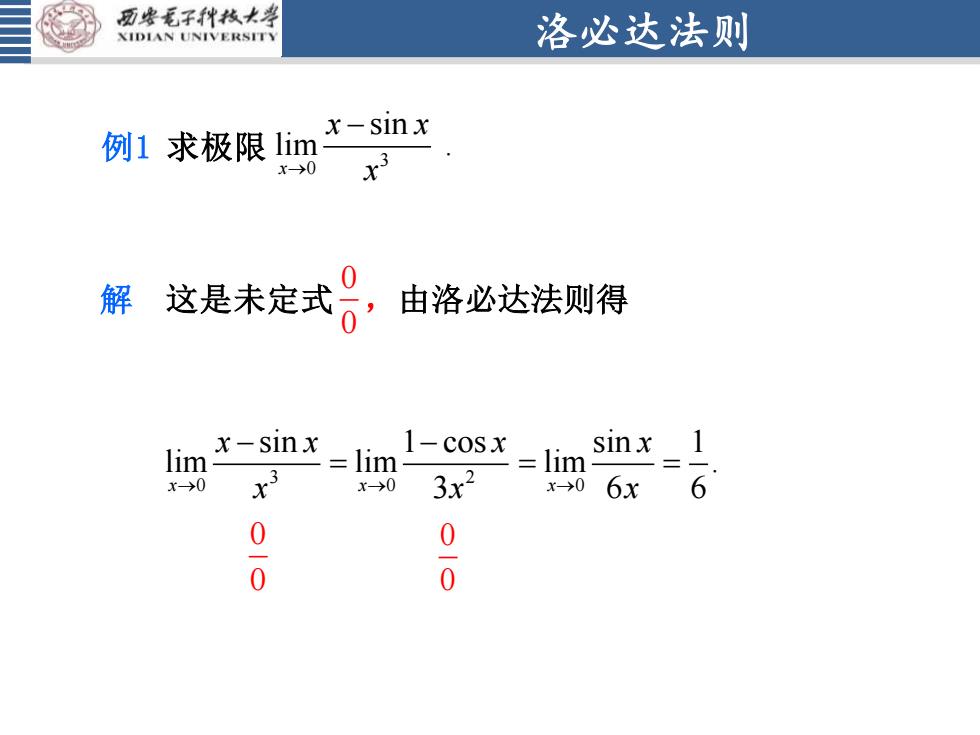
洛必达法则 例1 求极限 3 0 sin lim . x x x → x− 这是未定式 ,由洛必达法则得 0 0 0 sin 1 lim . → 6 6 = = x x x 解 3 0 sin lim → − x x x x 2 0 1 cos lim x 3 x → x − = 0 0 0 0
西安毛子科技大学洛必达法则XIDIANUNIVERSITS-2x-ex例2求极限limx->0x-sinx0解这是未定式由洛必达法则得0ere-x2xe*+0-x-2limlim1-6x->0x->0Cosxx-sinxee'+e-xet= lim lim2x-→0x->0sin xcos x00
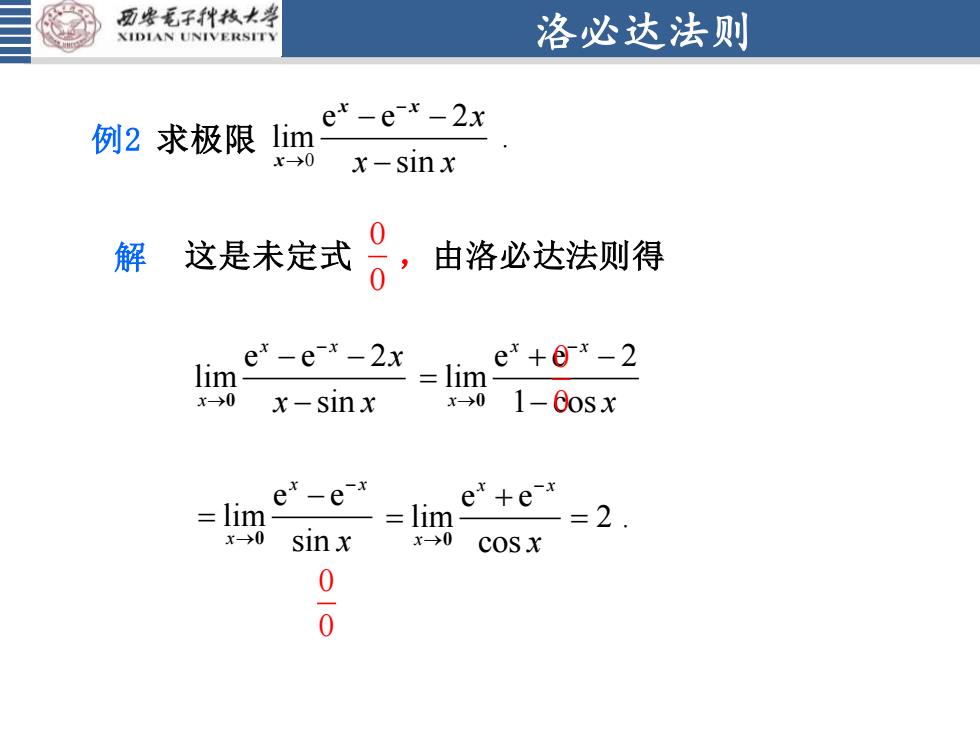
洛必达法则 例2 求极限 0 e e 2 lim . sin x x x − → − − − x x x 这是未定式 ,由洛必达法则得 0 0 e e 2 lim 1 cos x x x x − → + − = 0 − e e lim cos x x x x − → + = 0 解 e e lim sin x x x x − → − = 0 = 2 . e e 2 lim sin x x x x x x − → − − 0 − 0 0 0 0

西安毛子科技大学洛必达法则XIDIAN UNIVERSITY(tan x -x)cosx例3求极限limx→0xsin x2解由于x→0时,sinx2~x2,并且 limcosx=1,所以(tan x - x)cos x0tan x- xlim= lim洛必达法则x sin x?x.x?x→00x-→0sec2x-1= lim3x2x-→01tan? x= lim3x23x-→>0
洛必达法则 例3 求极限 2 0 (tan )cos lim . x sin x x x → x x − 由于 x → 0 时, sin , x x 2 2 并且 limcos 1, x→0 x = 所以 0 2 (tan ) lim cos x sin x x x x → x − 2 2 0 sec 1 lim x 3 x → x − = 2 2 0 tan lim x 3 x → x = 解 0 2 tan lim x x x x → x − = 1 . 3 = 洛必达法则 0 0
西安毛子科技大学洛必达法则XIDIANUNIVERSITY注 对于 x→at,x→a 以及x→0,x→+,x→-8 时,0未定式号有相应结论。元arctan x2例4求极限lim1x→+00x0解当x→+8时,这是未定式由洛必达法则得O1元arctan xx?1+x?2lim= lim=1.lim11x→+0 1 + x?X->+00x-→+o0xx
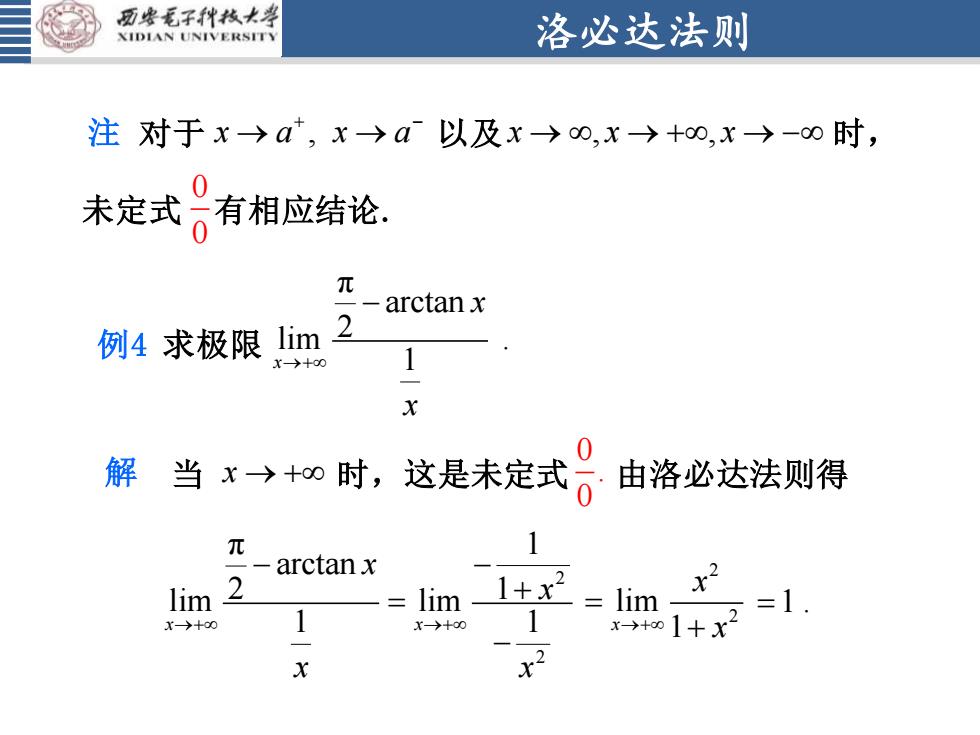
洛必达法则 对于 x a x a , 以及 时, → → + − x x x → → + → − , , 未定式 有相应结论. 0 0 例4 求极限 π arctan 2 lim . x 1 x x →+ − 当 x → + 时,这是未定式 由洛必达法则得 0 . 0 π arctan 2 limx 1 x x →+ − 注 解 2 2 lim x 1 x →+ x = + 2 2 1 1 lim →+ 1 − + = − x x x =1