在哥尼斯堡的一个公园里, 有七座桥將普雷格尔河中两 个岛及岛与河岸连接起来(如 图)。问是否可能从这四块陆 地中任一块出发,恰好通过 每座桥一次,再回到起点? 哥尼斯堡(Koni gsberg) 七桥问题
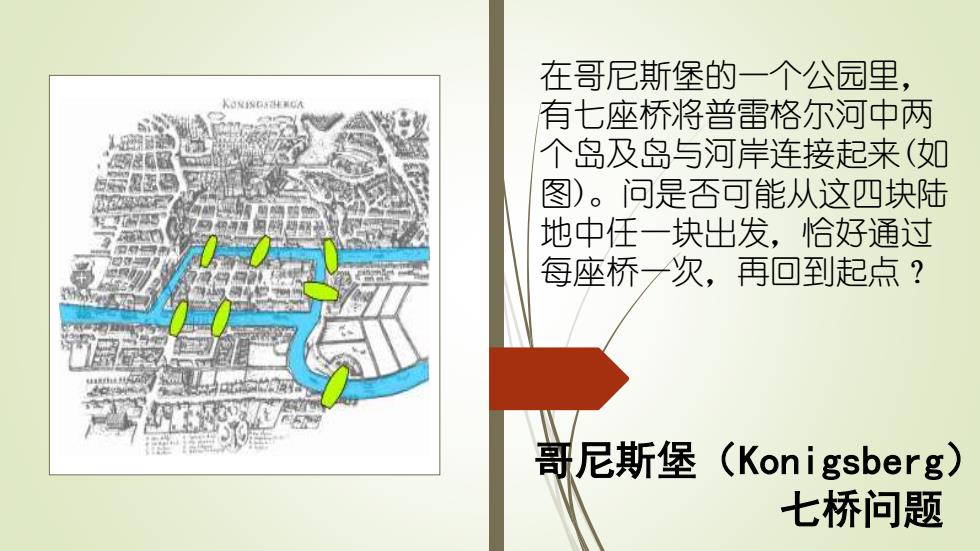
在哥尼斯堡的一个公园里, 有七座桥将普雷格尔河中两 个岛及岛与河岸连接起来(如 图)。问是否可能从这四块陆 地中任一块出发,恰好通过 每座桥一次,再回到起点? 哥尼斯堡(Konigsberg) 七桥问题

1736年29岁的欧拉向圣彼得堡科学院递交了《哥 尼斯堡的七座桥》的报告,在解答问题的同时, 开创了数学的一个新的分支一图论,也由此展 开了数学史上的新历程。 欧拉的论文《Solutio problematis ad geometriam situs pertinentis/The solution of a problem relating to the geometry of position/ 据几何位置的解题方法》1741年发表于《Journal Commentarii academiae scientiarum Petropolitanae》 这是关于图论的第一篇论文
1736年29岁的欧拉向圣彼得堡科学院递交了《哥 尼斯堡的七座桥》的报告,在解答问题的同时, 开创了数学的一个新的分支——图论,也由此展 开了数学史上的新历程。 欧拉的论文《Solutio problematis ad geometriam situs pertinentis /The solution of a problem relating to the geometry of position/依 据几何位置的解题方法》1741年发表于《Journal Commentarii academiae scientiarum Petropolitanae》。 ——这是关于图论的第一篇论文
每一块陆地考虑成一个点 连接两块陆地的桥以线(边)表示 A B 因为点A关联了5条边,即与岛A相连接的有5座桥, 故这些桥不可能每座恰好被走过1次
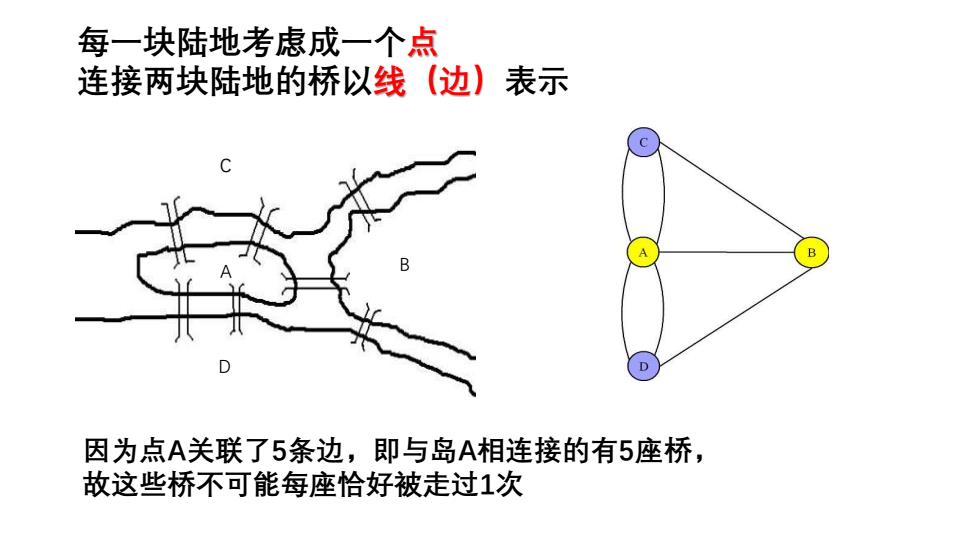
每一块陆地考虑成一个点 连接两块陆地的桥以线(边)表示 因为点A关联了5条边,即与岛A相连接的有5座桥, 故这些桥不可能每座恰好被走过1次 C A B D

再论七桥问题:从图的基本概念说起 图的定义 一个图G是一个有序二元组(V,),其中 )V是一个有限的非空集合,称为顶点集合,其 元素称为顶点或点。用V或v(G)或v表示顶点数; (2)E是由V中的点组成的无序对构成的集合,称 为边集,其元素称为边,且同一点对在E中可以 重复出现多次。用|E或e(G)或e表示边数
再论七桥问题:从图的基本概念说起 图的定义 (1) V是一个有限的非空集合,称为顶点集合,其 元素称为顶点或点。用|V|或v(G)或υ表示顶点数; (2) E是由V中的点组成的无序对构成的集合,称 为边集,其元素称为边,且同一点对在E中可以 重复出现多次。用|E|或e(G)或ε表示边数。 一个图G是一个有序二元组(V, E),其中

相邻:同一条边的两个端点称为相邻 关联:一条边的端点和边关联 环:端点重合的边 重边:端点相同的边(两条以上) 有限图:顶点集和边集都是有限的图 平凡图:只有一个项点的图 简单图:不含重边和环的图
相邻:同一条边的两个端点称为相邻 环:端点重合的边 重边:端点相同的边(两条以上) 有限图:顶点集和边集都是有限的图 平凡图:只有一个顶点的图 简单图:不含 和 的图 关联:一条边的端点和边关联