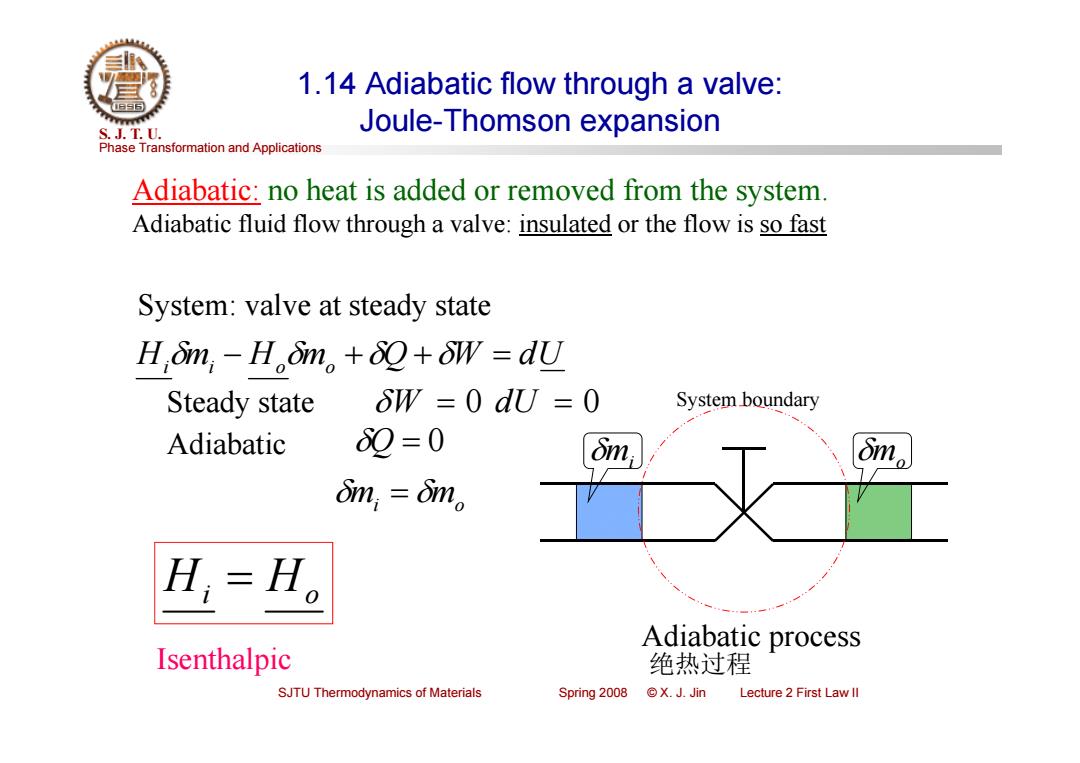
1.14 Adiabatic flow through a valve: S.J.T.0. Joule-Thomson expansion Phase Transformation and Applications Adiabatic:no heat is added or removed from the system. Adiabatic fluid flow through a valve:insulated or the flow is so fast System:valve at steady state H,mn,-H.m。++δW=dU Steady state 8W=0dJ=0 System boundary Adiabatic 89=0 on dim,=6im。 L=H。 Adiabatic process Isenthalpic 绝热过程 SJTU Thermodynamics of Materials Spring 2008 ©X.J.Jin Lecture 2 First Law ll
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 2 First Law II 1.14 Adiabatic flow through a valve: Joule-Thomson expansion System: valve at steady state Himi Homo Q W dU Adiabatic Q 0 mi mo Hi Ho Isenthalpic System boundary mi mo Adiabatic process 绝热过程 Steady state W 0 dU 0 Adiabatic: no heat is added or removed from the system. Adiabatic fluid flow through a valve: insulated or the flow is so fast
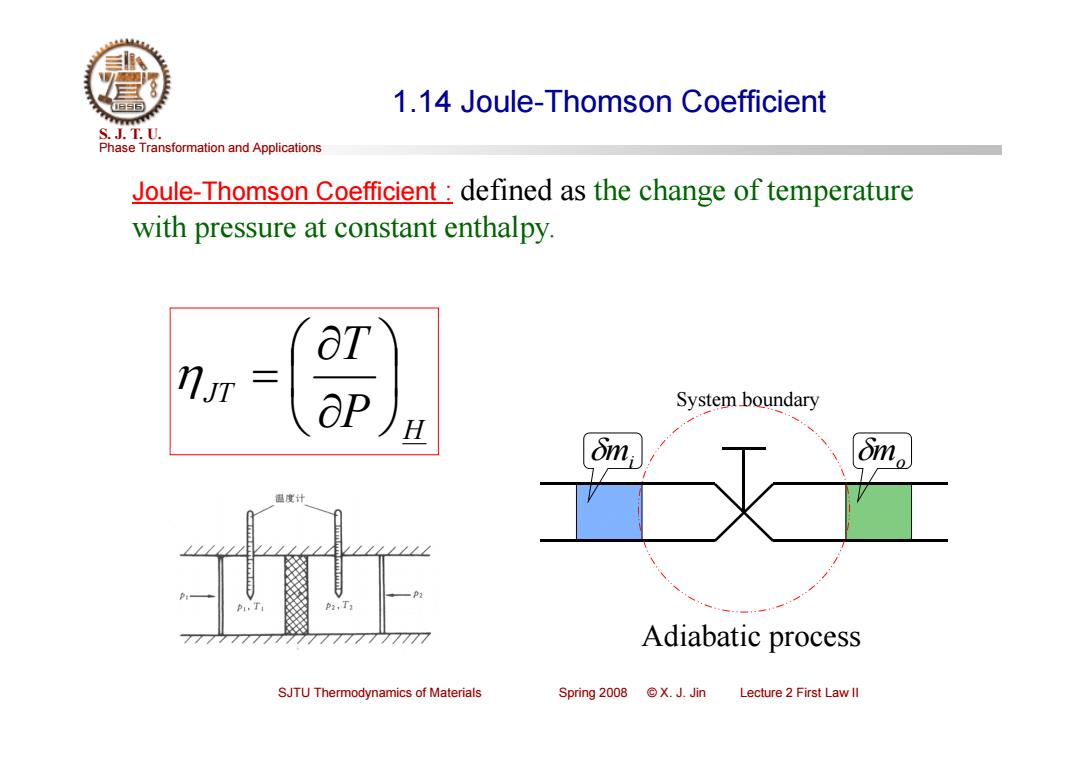
1.14 Joule-Thomson Coefficient S.J.T.0. Phase Transformation and Applications Joule-Thomson Coefficient defined as the change of temperature with pressure at constant enthalpy. ot aP System boundary H dm 国度计 P2,T 7777777777 Adiabatic process SJTU Thermodynamics of Materials Spring2008©X.J.Jin Lecture 2 First Law ll
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 2 First Law II 1.14 Joule-Thomson Coefficient Joule-Thomson Coefficient : defined as the change of temperature with pressure at constant enthalpy. System boundary mi mo H JT P T Adiabatic process

1.15 Equations of State (1) S.J.T.0. Phase Transformation and Applications Equations of state:the relationship among the physical variables that describe the condition of a material. For gases:the relationship between pressure(P),volume (V), temperature (T)and number of moles (n). PV=nRT PV=RT R:the universal gas constant:8.314 J/(mol.K) One mole of gas at 273.15 K and one atmosphere V=22.4L/mol 状态方程 理想气体的状态方程 SJTU Thermodynamics of Materials Spring 2008 X.J.Jin Lecture 2 First Law ll
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 2 First Law II 1.15 Equations of State (1) Equations of state : the relationship among the physical variables that describe the condition of a material. For gases : the relationship between pressure (P), volume (V), temperature (T) and number of moles (n). PV nRT PV RT R : the universal gas constant: 8.314 J/(molK). V 22.4L / mol One mole of gas at 273.15 K and one atmosphere 状态方程 理想气体的状态方程
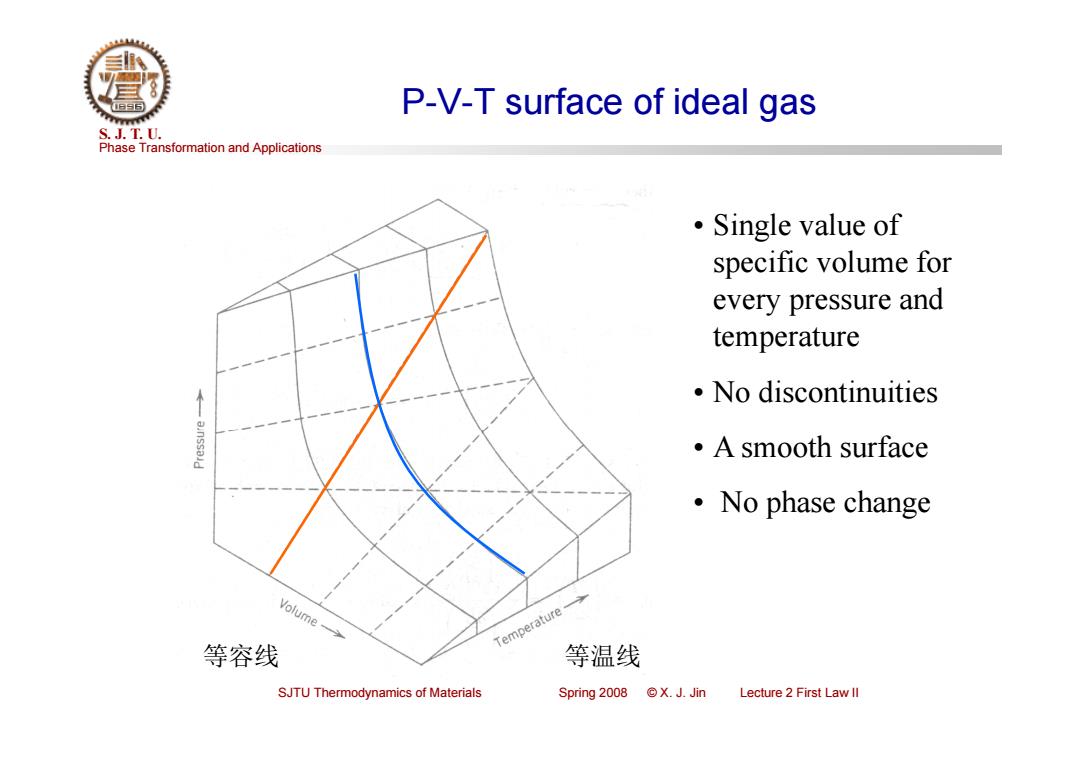
P-V-T surface of ideal gas S.J.T.0. Phase Transformation and Applications ·Single value of specific volume for every pressure and temperature 。No discontinuities ·A smooth surface ·No phase change Volume- Temperature 等容线 等温线 SJTU Thermodynamics of Materials Spring 2008 X.J.Jin Lecture 2 First Law ll
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 2 First Law II P-V-T surface of ideal gas • Single value of specific volume for every pressure and temperature • No discontinuities • A smooth surface • No phase change 等容线 等温线
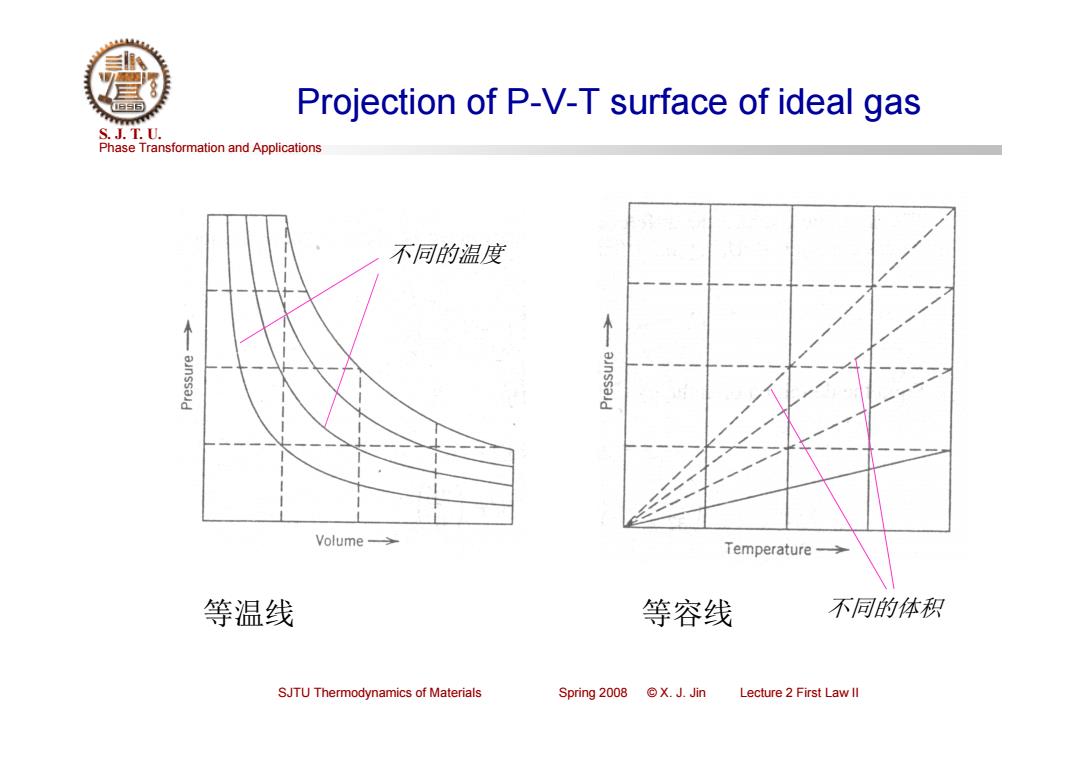
Projection of P-V-T surface of ideal gas S.J.T.0. Phase Transformation and Applications 不同的温度 Volume-> Temperature-> 等温线 等容线 不同的体积 SJTU Thermodynamics of Materials Spring 2008 X.J.Jin Lecture 2 First Law ll
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2008 © X. J. Jin Lecture 2 First Law II Projection of P-V-T surface of ideal gas 等温线 等容线 不同的温度 不同的体积