
Definition Example If ej is a canonical vector,then lelp=1forp≥1. If e=(1 1...1)ER,then llell1 =n,lelloo =1,llellp nP,1<ps co. 命电有这女子 Matrix Theory Vector Norms -7/39
Definition Example ▸ If ej is a canonical vector, then ∥ej∥ p = 1 for p ≥ 1. ▸ If e = ( 1 1 . . . 1 ) T ∈ R n , then ∥e∥1 = n, ∥e∥∞ = 1, ∥e∥p = n 1/p , 1 < p ≤ ∞. Matrix Theory Vector Norms - 7/39
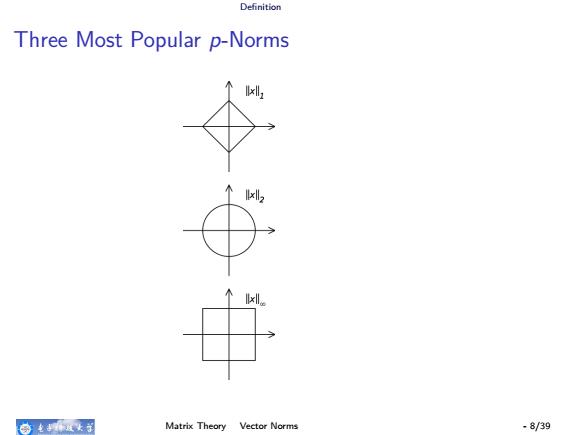
Definition Three Most Popular p-Norms 命电有这女 Matrix Theory Vector Norms -8/39
Definition Three Most Popular p-Norms Matrix Theory Vector Norms - 8/39
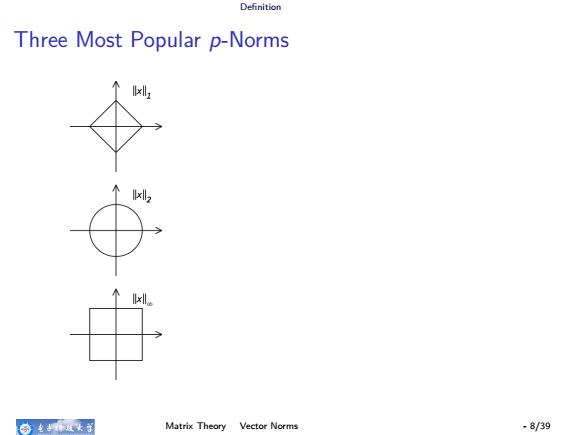
Definition Three Most Popular p-Norms x 务老环这女子 Matrix Theory Vector Norms -8/39
Definition Three Most Popular p-Norms One norm: ∥x∥1 = ∑ n j=1 ∣x∣j . Two (or Euclidean) norm: ∥x∥2 = √ ∑ n j=1 ∣x∣ 2 j = √ x Hx. Infinity (or maximum) norm: ∥x∥∞ = max1≤j≤n ∣xj ∣. Matrix Theory Vector Norms - 8/39
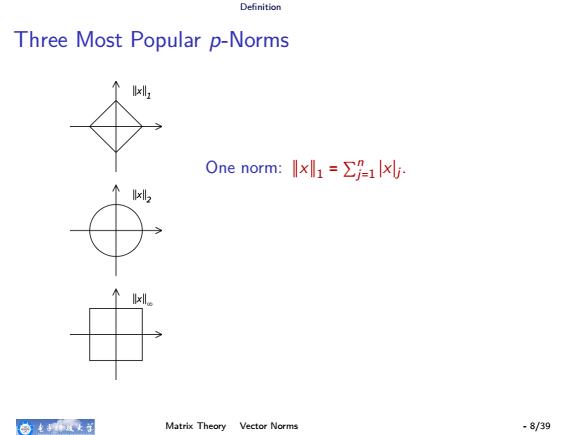
Definition Three Most Popular p-Norms One norm:x= x 务老环这女子 Matrix Theory Vector Norms -8/39
Definition Three Most Popular p-Norms One norm: ∥x∥1 = ∑ n j=1 ∣x∣j . Two (or Euclidean) norm: ∥x∥2 = √ ∑ n j=1 ∣x∣ 2 j = √ x Hx. Infinity (or maximum) norm: ∥x∥∞ = max1≤j≤n ∣xj ∣. Matrix Theory Vector Norms - 8/39

Definition Three Most Popular p-Norms One norm:lx1=∑x刘 Two (or Euclidean)norm: Ix2=V√∑x灯=VxHx 务老环这女子 Matrix Theory Vector Norms -8/39
Definition Three Most Popular p-Norms One norm: ∥x∥1 = ∑ n j=1 ∣x∣j . Two (or Euclidean) norm: ∥x∥2 = √ ∑ n j=1 ∣x∣ 2 j = √ x Hx. Infinity (or maximum) norm: ∥x∥∞ = max1≤j≤n ∣xj ∣. Matrix Theory Vector Norms - 8/39