Definition Example 奇电有这头 Matrix Theory Vector Norms -7/39
Definition Example ▸ If ej is a canonical vector, then ∥ej∥ p = 1 for p ≥ 1. ▸ If e = ( 1 1 . . . 1 ) T ∈ R n , then ∥e∥1 = , ∥e∥∞ = , ∥e∥p = , 1 < p ≤ ∞. Matrix Theory Vector Norms - 7/39
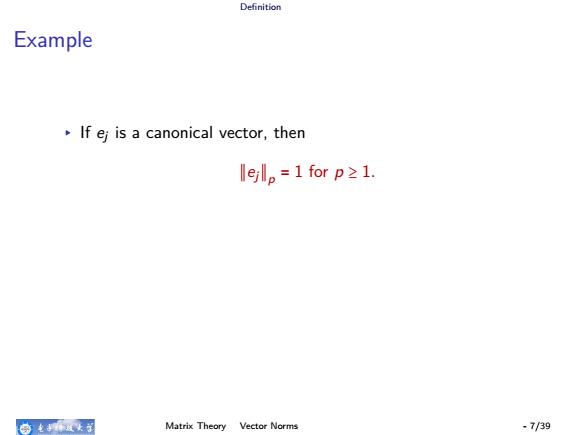
Definition Example If ej is a canonical vector,then llejlp =1 for p21. 命电有这女子 Matrix Theory Vector Norms -7/39
Definition Example ▸ If ej is a canonical vector, then ∥ej∥ p = 1 for p ≥ 1. ▸ If e = ( 1 1 . . . 1 ) T ∈ R n , then ∥e∥1 = , ∥e∥∞ = , ∥e∥p = , 1 < p ≤ ∞. Matrix Theory Vector Norms - 7/39

Definition Example If ej is a canonical vector,then lelp=1forp≥1. .If e=(1 1...1)ER,then llell1=,lellco =lellp=,1<ps oo. 奇电有头 Matrix Theory Vector Norms -7/39
Definition Example ▸ If ej is a canonical vector, then ∥ej∥ p = 1 for p ≥ 1. ▸ If e = ( 1 1 . . . 1 ) T ∈ R n , then ∥e∥1 = , ∥e∥∞ = , ∥e∥p = , 1 < p ≤ ∞. Matrix Theory Vector Norms - 7/39

Definition Example If ej is a canonical vector,then lelp=1forp≥1. .If e=(1 1...1)ER,then llell1=n,llelldo =lellp =1<ps oo. 奇电有这头 Matrix Theory Vector Norms -7/39
Definition Example ▸ If ej is a canonical vector, then ∥ej∥ p = 1 for p ≥ 1. ▸ If e = ( 1 1 . . . 1 ) T ∈ R n , then ∥e∥1 = n, ∥e∥∞ = , ∥e∥p = , 1 < p ≤ ∞. Matrix Theory Vector Norms - 7/39

Definition Example If ej is a canonical vector,then lelp=1forp≥1. .If e=(1 1...1)ER,then lell1 =n,lello =1,llellp=,1<ps oo. 命电有这女子 Matrix Theory Vector Norms -7/39
Definition Example ▸ If ej is a canonical vector, then ∥ej∥ p = 1 for p ≥ 1. ▸ If e = ( 1 1 . . . 1 ) T ∈ R n , then ∥e∥1 = n, ∥e∥∞ = 1, ∥e∥p = , 1 < p ≤ ∞. Matrix Theory Vector Norms - 7/39