
《数学分析》教案 第七章实数的完备性 海南大学数学系 第七章实数的完备性 §1实数完备性的等价命题 一、问题提出 定理11(确界原理)非空有上(下)界的数集必有上(下)确界. 确界存在定理(定理1.1)揭示了实数的连续性和实数的完备性.与之等价的还有五大命题 这就是以下的定理1.2至定理1.6. 定理1.2(单调有界定理)任何单调有界数列必定收敛. 定理1.3(区间套定理)设4,6,》为一区间套: [a,8 ]3[am.b12. 2照(6-4,)-0 则存在唯一一点∈[a点,],n-12,. 定理1.4(有限覆盖定理)设H-(化)是闭区间a,b]的一个无限开覆盖,即a,b] 中每一点都含于H中至少一个开区间(出8)内.则在H中必存在有限个开区间,它们构成a,b] 的一个有限开覆盖. 定理1.5(聚点定理)直线上的任一有界无限点集S至少有一个聚点片即在的任意小邻 域内都含有S中无限多个点(本身可以属于S,也可以不属于S). 定理1.6(柯西准则)数列0,收敛的充要条件是:Y>0,3NeN,只要m>,恒 有a“,K8.(后者又称为柯西(Cauchy)条件,满足柯西条件的数列又称为柯西列,或基 本列.) 这些定理构成极限理论的基础.我们不仅要正确理解这六大定理的含义,更重要的还要学会 怎样用它们去证明别的命题.下面通过证明它们之间的等价性,使大家熟悉使用这些理论工具, 下图中有三种不同的箭头,其含义如下: ◆,(1)~(3)基本要求类 (4)(7)阅读参考类
《数学分析》教案 第七章 实数的完备性 海南大学数学系 1 第七章 实数的完备性 §1 实数完备性的等价命题 一、问题提出 定理 1.1(确界原理)非空有上(下)界的数集必有上(下)确界. 确界存在定理(定理 1.1)揭示了实数的连续性和实数的完备性. 与之等价的还有五大命题, 这就是以下的定理 1.2 至定理 1.6. 定理 1.2 (单调有界定理) 任何单调有界数列必定收敛. 定理 1.3 (区间套定理) 设 为一区间套: . 则存在唯一一点 定理 1.4 (有限覆盖定理) 设 是闭区间 的一个无限开覆盖,即 中每一点都含于 中至少一个开区间 内.则在 中必存在有限个开区间,它们构成 的一个有限开覆盖. 定理 1.5 (聚点定理) 直线上的任一有界无限点集 至少有一个聚点 ,即在 的任意小邻 域内都含有 中无限多个点( 本身可以属于 ,也可以不属于 ). 定理 1.6 (柯西准则) 数列 收敛的充要条件是: ,只要 恒 有 .(后者又称为柯西(Cauchy)条件,满足柯西条件的数列又称为柯西列,或基 本列.) 这些定理构成极限理论的基础.我们不仅要正确理解这六大定理的含义,更重要的还要学会 怎样用它们去证明别的命题.下面通过证明它们之间的等价性,使大家熟悉使用这些理论工具. 下图中有三种不同的箭头,其含义如下: : (1)~(3) 基本要求类 : (4)~(7) 阅读参考类
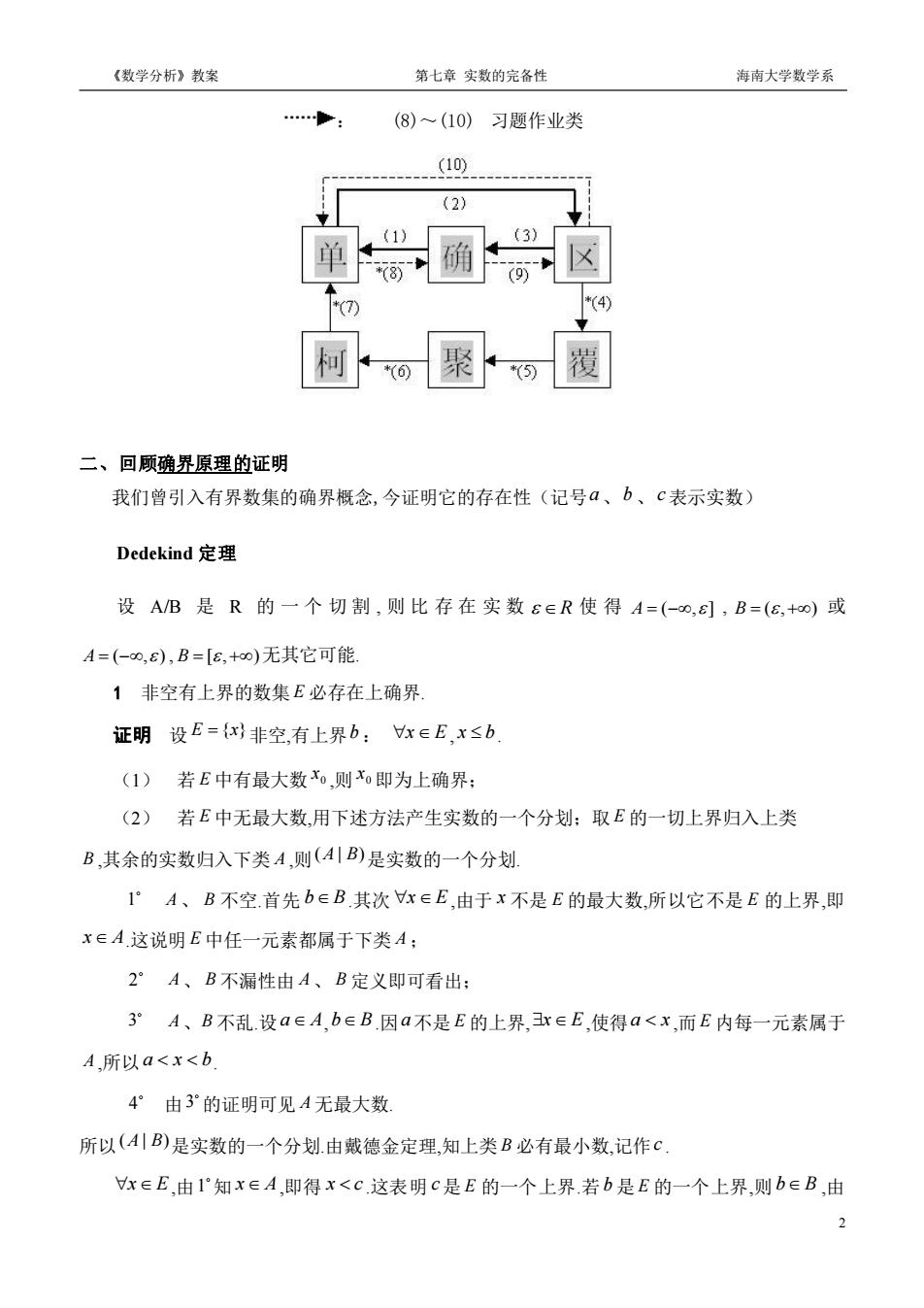
《数学分析》教案 第七章实数的完备性 海南大学数学系 (8)~(10)习题作业类 .-(10 (2 柯o聚o覆 二、回顾确界原理的证明 我们曾引入有界数集的确界概念,今证明它的存在性(记号a、b、c表示实数) Dedekind定理 设AB是R的一个切割,则比存在实数E∈R使得A=(-o,),B=(8,+o)或 A=(-o,s),B=【8,+o)无其它可能. 1非空有上界的数集£必存在上确界 证明设E={x非空,有上界b:x∈E,x≤b (1)若E中有最大数x,则x即为上确界: (2)若E中无最大数,用下述方法产生实数的一个分划:取E的一切上界归入上类 B,其余的实数归入下类A,则(4B)是实数的一个分划! 1°A、B不空首先bEB其次r∈E,由于x不是E的最大数,所以它不是E的上界,即 xEA这说明E中任一元素都属于下类A; 2°A、B不漏性由A、B定义即可看出: 3°A、B不乱.设aeA,b∈B.因a不是E的上界,3r∈E,使得a<x,而E内每一元素属于 A,所以a<x<b 4°由3°的证明可见A无最大数 所以(4川B)是实数的一个分划.由戴德金定理,知上类B必有最小数,记作C x∈E,由1“知x∈A,即得x<c这表明c是E的一个上界.若b是E的一个上界,则b∈B,由 2
《数学分析》教案 第七章 实数的完备性 海南大学数学系 2 : (8)~(10) 习题作业类 二、回顾确界原理的证明 我们曾引入有界数集的确界概念,今证明它的存在性(记号 a、b 、c 表示实数) Dedekind 定理 设 A/B 是 R 的 一 个 切 割 , 则 比 存 在 实 数 R 使 得 A = − ( , ] , B = + ( , ) 或 A = − ( , ) , B = + [ , ) 无其它可能. 1 非空有上界的数集 E 必存在上确界. 证明 设 E = {x} 非空,有上界 b : x E, x b. (1) 若 E 中有最大数 0 x ,则 0 x 即为上确界; (2) 若 E 中无最大数,用下述方法产生实数的一个分划;取 E 的一切上界归入上类 B ,其余的实数归入下类 A ,则 (A | B) 是实数的一个分划. 1 A、 B 不空.首先 bB.其次 x E,由于 x 不是 E 的最大数,所以它不是 E 的上界,即 x A.这说明 E 中任一元素都属于下类 A ; 2 A、 B 不漏性由 A 、 B 定义即可看出; 3 A、B 不乱.设 a A,bB.因 a 不是 E 的上界,xE,使得 a x ,而 E 内每一元素属于 A ,所以 a x b. 4 由 3 的证明可见 A 无最大数. 所以 (A | B) 是实数的一个分划.由戴德金定理,知上类 B 必有最小数,记作 c . x E,由 1 知 x A,即得 x c .这表明 c 是 E 的一个上界.若 b 是 E 的一个上界,则 bB ,由

《数学分析》教案 第七章实数的完备性 海南大学数学系 此得c≤b,所以c是上界中最小的,由上确界定义,c为集合E的上确界,记作c=spE 推论非空的有下界的集合必有下确界 事实上,设集合E=有下界b,则非空集合E=x-x∈B有上界-b,利用集合E'上确界 的存在性,即可得出集合£的下确界存在 定理1解决了非空有上界集合的上确界存在性问题,我们可以利用上确界的存在性,得出我们 所研究的某一类量(如弧长)的存在性 若全序集中任一非空有上界的集合必有上确界,我们称该全序集是完备的定理1刻划了实数 集是完备的 例1证明实数空间满足阿基米德原理 证明∀b>a>0,要证存在自然数n使a>b.假设结论不成立,即 a≤b,(m=l,2.) 则数集E={na}有上界b,因此有上确界c,使na≤c(m=l,2,.),也就有 (n+I)a≤c(n=,2,.),或na≤c-a(m=l2,.).这表明c-a是集合E的上界与c是上确 界矛盾.所以总存在自然数n,使na>b 三、等价命题证明 下面来完成(1)(7)的证明. (一)用确界定理证明单调有界定理 设,单调上升,即名≤名≤名≤.≤x≤.有上界,即3M,使得≤M 考虑集合E=化,nEN,它非空,有界,定理2推出它有上确界,记为a=即我们验证 a=lim x 6>0,由上确界的性质,3N,使得a-8<xx,当n>N时,由序列单调上升得a-8<xw≤x。, 再由上确界定义,x≤a<a+6,有a-6<x,<a+,即k,-d<6,也就是说血x=a=即, 同理可证若伍,}单调下降,有下界,也存在极限且血。,=赋无 若集合E无上界,记作supE=+0:若集合E无下界,记作fE=+o,这样一来定理2证明了 的单调上升(下降)有上界(下界)的序列,},必有极限即,矿)的定理现在有了严格的 理论基础了且对单调上升(下降)序列x},总有
《数学分析》教案 第七章 实数的完备性 海南大学数学系 3 此得 c b ,所以 c 是上界中最小的,由上确界定义, c 为集合 E 的上确界,记作 c = sup E . 推论 非空的有下界的集合必有下确界. 事实上,设集合 E = {x} 有下界 b ,则非空集合 E' = {x | −x E} 有上界−b ,利用集合 E' 上确界 的存在性,即可得出集合 E 的下确界存在. 定理 1 解决了非空有上界集合的上确界存在性问题,我们可以利用上确界的存在性,得出我们 所研究的某一类量(如弧长)的存在性. 若全序集中任一非空有上界的集合必有上确界,我们称该全序集是完备的.定理 1 刻划了实数 集是完备的. 例1 证明实数空间满足阿基米德原理. 证明 b a 0,要证存在自然数 n 使 na b .假设结论不成立,即 na b, (n = 1,2,), 则数集 E = {na} 有上界 b , 因此有上确界 c , 使 na c (n = 1,2,), 也就有 (n +1)a c (n = 1,2,),或 na c − a (n = 1,2,).这表明 c − a 是集合 E 的上界,与 c 是上确 界矛盾.所以总存在自然数 n ,使 na b . 三、等价命题证明 下面来完成(1)~(7)的证明. (一) 用确界定理证明单调有界定理 设 { }n x 单调上升,即 x1 x2 x3 xn ,有上界,即 M ,使得 xn M . 考虑集合 E {x | n N} = n ,它非空,有界,定理 2 推出它有上确界,记为 n n N a x = sup .我们验证 n n a x → = lim . 0 ,由上确界的性质, N ,使得 N a − x ,当 n N 时,由序列单调上升得 N n a − x x , 再由上确界定义, x a a + n ,有 a − x a + n ,即 x − a n ,也就是说 n n N n n x a x → lim = = sup . 同理可证若 { }n x 单调下降,有下界,也存在极限,且 n n N n n x x → lim = inf . 若集合 E 无上界,记作 sup E = + ;若集合 E 无下界,记作 inf E = + ,这样一来,定理 2 证明了 的单调上升(下降)有上界(下界)的序列 { }n x ,必有极限 sup (inf ) n x N n x N x x 的定理现在有了严格的 理论基础了.且对单调上升(下降)序列 { }n x ,总有

《数学分析》教案 第七章实数的完备性 海南大学数学系 mxm=spx。(nfxa) (仁)用单调有界定理证明区间套定理 由假设(1)知,序列a,}单调上升,有上界6:序列b,}单调下降,有下界4.因而有 lman=c1mb,=c3an≤G≤c2≤bn 再由假设(2)知 lim (b-a)=c2-C=0 记9=G2=C.从而有 lim d =c=lim b 若还有c满足a,≤c≤b,令n→切,得c=c,故c是一切ab,小的唯一公共点.证毕, 这个定理称为区间套定理.关于定理的条件我们作两点说明: (1)要求[a,b,]是有界闭区间的这个条件是重要的.若区间是开的,则定理不一定成立, 如 a6,)=0, 显然有@,c0为,但iQ=4 如果开区间套是严格包含:a,<a1<b<b,这时定理的结论还是成立的, 2)若o.blCIo.b,1a=12.),但m。-a,)0,此时仍有 皿a,=6,m6=6,但<6,于是对任意的c,S≤c≤C,都有ce0ab] 全序集中任一区间长趋于零的区间套有非空交集,则称该全序集是完备的,定理3刻划实 数集是完备的(这里完备定义与上段完备定义是等价的).定理3也给出通过逐步缩小搜索范围, 找出所求点的一种方法. 推论设a点.]》为一区间套,e[a.4]-12,.则e>03NeN,当n>N时,恒 有 [a,b]cU(点 用区间套定理证明其他命题时,最后常会用到这个推论
《数学分析》教案 第七章 实数的完备性 海南大学数学系 4 lim sup (inf ) n x N n x N n n x x x →+ = . (二) 用单调有界定理证明区间套定理 由假设(1)知,序列 { }n a 单调上升,有上界 1 b ;序列 { }n b 单调下降,有下界 1 a .因而有 1 lim a c n n = →+ , 2 lim b c n n = →+ . n bn a c1 c2 . 再由假设(2)知 lim ( − ) = 2 − 1 = 0 →+ b a c c n n n , 记 c = c = c 1 2 . 从而有 n n n n a c b →+ →+ lim = = lim . 若还有 * c 满足 n bn a c * ,令 n → +,得 c = c * .故 c 是一切 [ , ] an bn 的唯一公共点.证毕. 这个定理称为区间套定理.关于定理的条件我们作两点说明: (1) 要求 [ , ] an bn 是有界闭区间的这个条件是重要的.若区间是开的,则定理不一定成立. 如 ) 1 ( , ) (0, n an bn = . 显然有 ) 1 ) (0, 1 1 (0, n n + , 但 = + = ) 1 (0, n 1 n . 如果开区间套是严格包含: an an+1 bn+1 bn ,这时定理的结论还是成立的. (2)若 [ , ] [ , ] an+1 bn+1 an bn (n = 1,2,),但 lim ( − ) 0 →+ n n n b a ,此时仍有 1 lim a c n n = →+ , 2 lim b c n n = →+ ,但 1 2 c c ,于是对任意的 c , 1 2 c c c ,都有 [ , ] 1 n n n c a b + = . 全序集中任一区间长趋于零的区间套有非空交集,则称该全序集是完备的,定理 3 刻划实 数集是完备的(这里完备定义与上段完备定义是等价的).定理 3 也给出通过逐步缩小搜索范围, 找出所求点的一种方法. 推论 设 为一区间套, .则 当 时,恒 有 . 用区间套定理证明其他命题时,最后常会用到这个推论.

《数学分析》教案 第七章实数的完备性 海南大学数学系 例2序列x}由下列各式 =0.5=6,=a-34同 2 所确定(见下图).证明极限血存在,并求此极限。 内巧4→x 证明当a=b时,。=0,故血,=a 当a≠b时,若取an=min),bn=max1,xn),(n=l,2,.) 则由条件,显然可得一串区间套: [a,b]c[a,b](n=12,.) 由已知条件 -+-,=-) 2 于是 6-a,xa-,上l-x上1x-x ==2是l-x卡21b-a0a→4m 由区间套定理,存在c满足:血a,=c-血6,注意到,e口,b】,所以m=c 下面来求.由或-令”=23k-1得一串等式 -名=-,-), x-=-3-x) x-=-2-)
《数学分析》教案 第七章 实数的完备性 海南大学数学系 5 例2 序列 { }n x 由下列各式 x1 = a , x2 = b , 2 −1 + −2 = n n n x x x (n = 3,4,) 所确定(见下图).证明极限 n n x →+ lim 存在,并求此极限. 1 x 3 x 5 x 4 x 2 x x 证明 当 a = b 时, xn = a ,故 xn a n = →+ lim . 当 a b 时,若取 min( , ) n n 1 n a x x = + , max( , ) n n 1 n b x x = + , (n = 1,2,). 则由条件,显然可得一串区间套: [ , ] [ , ] an+1 bn+1 an bn (n = 1,2,). 由已知条件 ( ) 2 1 2 1 1 1 − − + − = − − + − = n n n n n n n x x x x x x x , 于是 | | 0 ( ), 2 1 | | 2 1 | | 2 1 | | 2 1 | | 1 2 1 1 1 1 2 1 2 = = − = − → → + − = − = − = − − − + − − − x x b a n b a x x x x x x n n n n n n n n n n 由区间套定理,存在 c 满足: n n n n a c b →+ →+ lim = = lim .注意到 [ , ] n an bn x ,所以 x c n n = →+ lim . 下面来求 c .由 ( ) 2 1 n+1 − n = − n − n−1 x x x x ,令 n = 2,3,,k −1 得一串等式: ( ) 2 1 3 2 2 1 x − x = − x − x ; ( ) 2 1 4 3 3 2 x − x = − x − x ; ( ) 2 1 k − k−1 = − k−1 − k−2 x x x x