石河子大学：《计量经济学》课程PPT教学课件（硕士生）第九章 时间序列计量经济学模型的理论与方法 9.2 随机时间序列分析模型

AR(2)模型 X,=p1X,-1+p2X,-2+8, 对应的特征方程1-01Z-02z2=0的两个根z1、z2满足： Z122-1/02,Z1+z2=-01/02 解出φ1，p2 p2、1 见，=+3 2122 2122 由AR(2)的平稳性，lp2F1/2I|z2k1,则至少有一个根 的模大于1，不妨设忆>1，有 9,+0,=+-1=1-0-1X1-马)<1 21222122 1-1X1-马)>0 21 是z2P1。由p2-p1<1可推出同样的结果。 21

21 对应的特征方程1-1z-2z 2=0 的两个根z1、z2满足： z1z2 =-1/2 , z1+z2 =-1/2 Xt Xt Xt t =  + +  1 −1 2 −2 AR(2)模型 解出1，2 1 2 2 1 z z  = − 1 2 1 2 1 z z z + z  = 由AR(2)的平稳性，|2 |=1/|z1||z2 |<1 ，则至少有一个根 的模大于1，不妨设|z1|>1，有 ) 1 1 )(1 1 1 (1 1 1 2 1 2 1 2 1 2 1 2 − = − − −  + + = z z z z z z z z   ) 0 1 )(1 1 (1 1 2 − −  z z 于是| z2 |>1。由 2 - 1 <1可推出同样的结果

对高阶自回模型AR(p)来说，多数情况下没有必要直 接计算其特征方程的特征根，但有一些有用的规则可用 来检验高阶自回归模型的稳定性： (1)AR(p)模型稳定的必要条件是： p1+φ2+.+0<1 (2)由于0：(i=1,2,.p)可正可负，AR(p)模 型稳定的充分条件是： p1+p2+.+pp<1 22

22 对高阶自回模型AR(p)来说，多数情况下没有必要直 接计算其特征方程的特征根，但有一些有用的规则可用 来检验高阶自回归模型的稳定性： (1)AR(p)模型稳定的必要条件是： 1+2++p<1 (2)由于i(i=1,2,p)可正可负，AR(p)模 型稳定的充分条件是： |1|+|2|++|p|<1

例5.2.2：考察如下四个模型的平稳性 (1)x,=0.8x-1+8 (2)x,=-1.1x-1+8 (3)x,=x-1-0.5x-2+E (4)x,=x-1+0.5x-1+8, 23

23 例5.2.2:考察如下四个模型的平稳性 1 (1) 0.8 t t t x x  = + − 1 (2) 1.1 t t t x x  = − + − 1 2 (3) 0.5 t t t t x x x  = − + − − t t t t x = x + x +  −1 5 −1 (4) 0

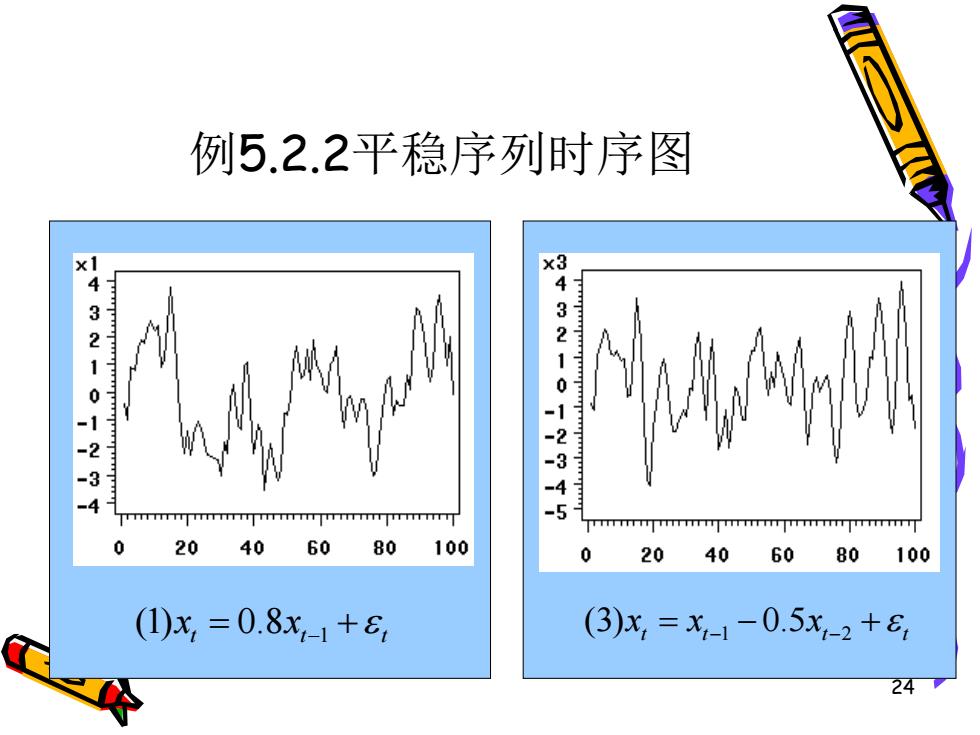
例5.2.2平稳序列时序图 xl x3 432 432. 1 0 -3 -4 20 4060 80 100 20406080100 (1)x,=0.8x-1+8 (3)x,=x-1-0.5x,-2+8 24

24 例5.2.2平稳序列时序图 1 (1) 0.8 t t t x x  = + − 1 2 (3) 0.5 t t t t x x x  = − + − −

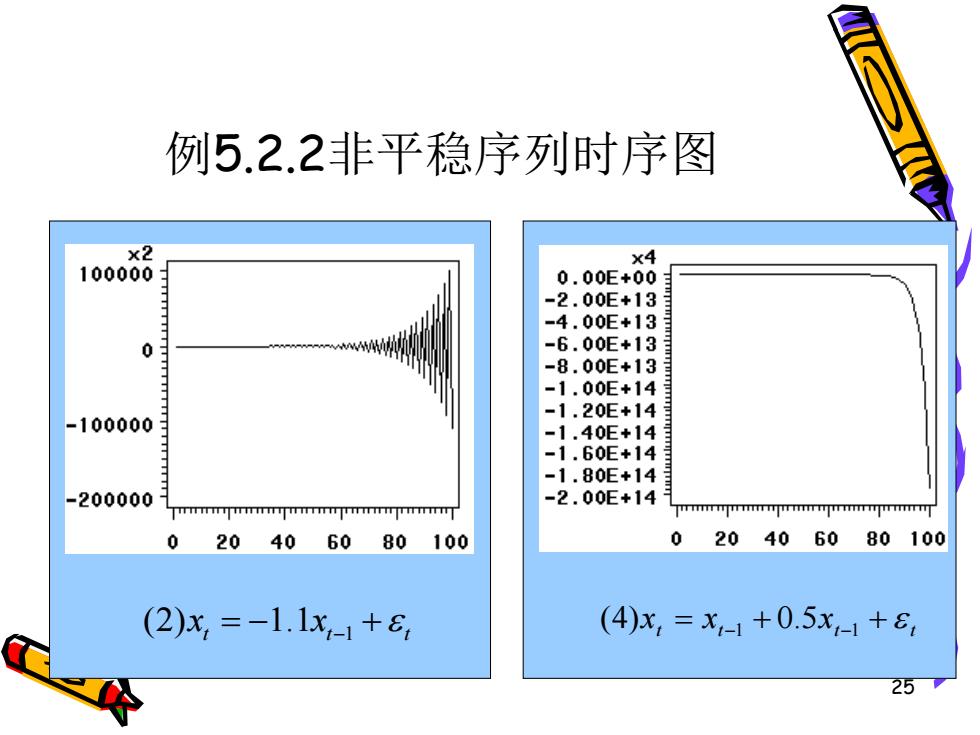
例5.2.2非平稳序列时序图 x2 x4 100000 0.00E+00 -2.00E+13 =4.00E+13 0 -6.00E+13 -8.00E+13 -1.00E+14 -1.20E+14 -100000 -1.60E+14 -1.80E+14 -200000 -2.00E+14 jmmnmmnjmmnimnmmn 0 20406080100 020406080100 (2)x,=-1.1x-1+c (4)x,=x-1+0.5x-1+ 25

25 例5.2.2非平稳序列时序图 1 (2) 1.1 t t t x x  = − + − t t t t x = x + x +  −1 5 −1 (4) 0