新疆大学：《自动控制理论》课程教学课件（PPT讲稿）第八章 非线性控制系统

自动控制理论 第二节 非线性元件的描述函数 米描述函数 r(0 e(t) G( 图8-6非线性控制系统 图中G(S)为线性环节，为非线性元件.若在N的输入端施加一幅值为X 频率为w的正统信号，即e=Xsinwt,则其输出为： y=A+4 sin ot+B cosot+4 sin 2ot+B2 cos2ot+. 假设： 1)非线性元件的特性对坐标原点是奇对称的，即A,=0 2)R()=0 3)G(s)具有良好的低通滤波器特性，能把y中多高次谐波滤掉，只 剩一次谐波项。 第八章非线性控制系统 2025/1/14

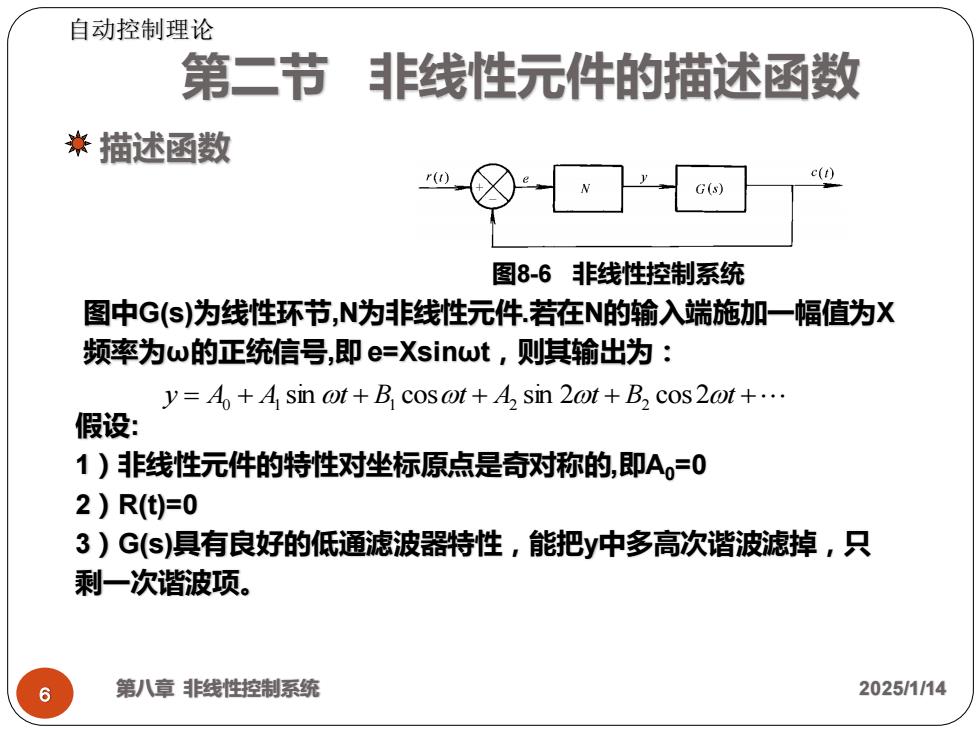
y = A0 + A1 sin t + B1 cost + A2 sin 2t + B2 cos2t + 第八章 非线性控制系统 2025/1/14 6 描述函数 图8-6 非线性控制系统 图中G(s)为线性环节,N为非线性元件.若在N的输入端施加一幅值为X 频率为ω的正统信号,即 e=Xsinωt，则其输出为： 第二节 非线性元件的描述函数 假设: 1）非线性元件的特性对坐标原点是奇对称的,即A0=0 2）R(t)=0 3）G(s)具有良好的低通滤波器特性，能把y中多高次谐波滤掉，只 剩一次谐波项。 自动控制理论

自动控制理论 则 Jy=A sin ot-+B,cos@t=Ysin(ot+Φ，) 其中 ==arctan ysiawtd(ot)） B= ycosotd(ot) 经过线性化处理后，非线性元件的输出是一个与其输入信号同频率的 正弦函数，仅在幅值和相位上与输入信号有差异。 非线性特性线性化的条件： 1)假设系统的输入)=0 2)非线性元件的静特性不是时间t的函数 3)非线性元件的特性是奇对称的，即有 f(e)=-f(-e) 第八章非线性控制系统 2025/1/14

( ) 1 1 1 1 y = A sint + B cost =Y sin t + ( ) B y td( t) A ysia td t A B Y A B          cos 1 1 , arctan 2 0 1 2 0 1 1 1 1 2 1 2 1 1   = = = + = 第八章 非线性控制系统 2025/1/14 7 则 其中 经过线性化处理后，非线性元件的输出是一个与其输入信号同频率的 正弦函数，仅在幅值和相位上与输入信号有差异。 非线性特性线性化的条件： 1）假设系统的输入r(t)=0 2）非线性元件的静特性不是时间t的函数 3）非线性元件的特性是奇对称的，即有 f (e)= − f (−e) 1 1 自动控制理论