中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第六章 傅里叶变换的应用

§6.1傅里叶系统函数 -微分方鞋向小-公C80=说积0 →D(p)y()=N(p)v(t) y(0),…,y(0)在零状态时为0， y(0),…,yn-(0,)在零状态时不为0 7

7 §6.1 傅里叶系统函数 – 微分方程：由             ,   N p N p H p y t v t D p D p                       1 1 0 , , 0 0, 0 , , 0 0 n n D p y t N p v t y y y y         在零状态时为 在零状态时不为

§6.1傅里叶系统函数 ·2.矩阵An,dt(2l-A)=0→，…，2特征根 A5,=25,0≠5∈R”,i∈{1,2，…，n},5为n个 线性无关的特征向量。 span{51,…,5n},X∈R”,X=x151+252+…+an5m X=4∑5=∑a45,=2a25谱方法 8

8 §6.1 傅里叶系统函数 • 2.矩阵 ……谱方法 A I A n n n * 1 , det 0 , ,        特征根 , , 1,2, ,   n A R i n n i i i i i         0 , 为 个 线性无关的特征向量。  1 1 1 2 2  1 1 1 span , , , , n n n n n n n i i i i i i i i i i R A A A                              X X= X =

§6.1傅里叶系统函数 v() T:H(s) -0川片0=空e心引 n=-c0 BIBO稳定 +00 y()=Tv()=∑VTem=∑，H(jn@)ee n=-o0 n=-0 算子谱特征函数 与线性代数中的谱方法相对应。 (特征根) 9

9 §6.1 傅里叶系统函数 – 若 T:H(s) v t  Y t            1 1 1 1 1 1 1 1 j - j j 1 - - L , , , , , 2 2 2 2 j n t n n BIBO n t n t n n n n T T T T v t v t V e t y t Tv t V Te V H n e                                       稳定 则 与线性代数中的谱方法相对应。 算子谱 （特征根） 特征函数

§6.1傅里叶系统函数 -若v()∈L(-o,+o),则v()=V(o)edf, y(t)=Tv(t)=V(@)Teimdf =V(@)H(@)edf=h(t)*v(t) 10

10 §6.1 傅里叶系统函数 – 若                        + 1 j - + j - + j - L , , d , d d t t t v t v t V e f y t Tv t V Te f V H e f h t v t                          则

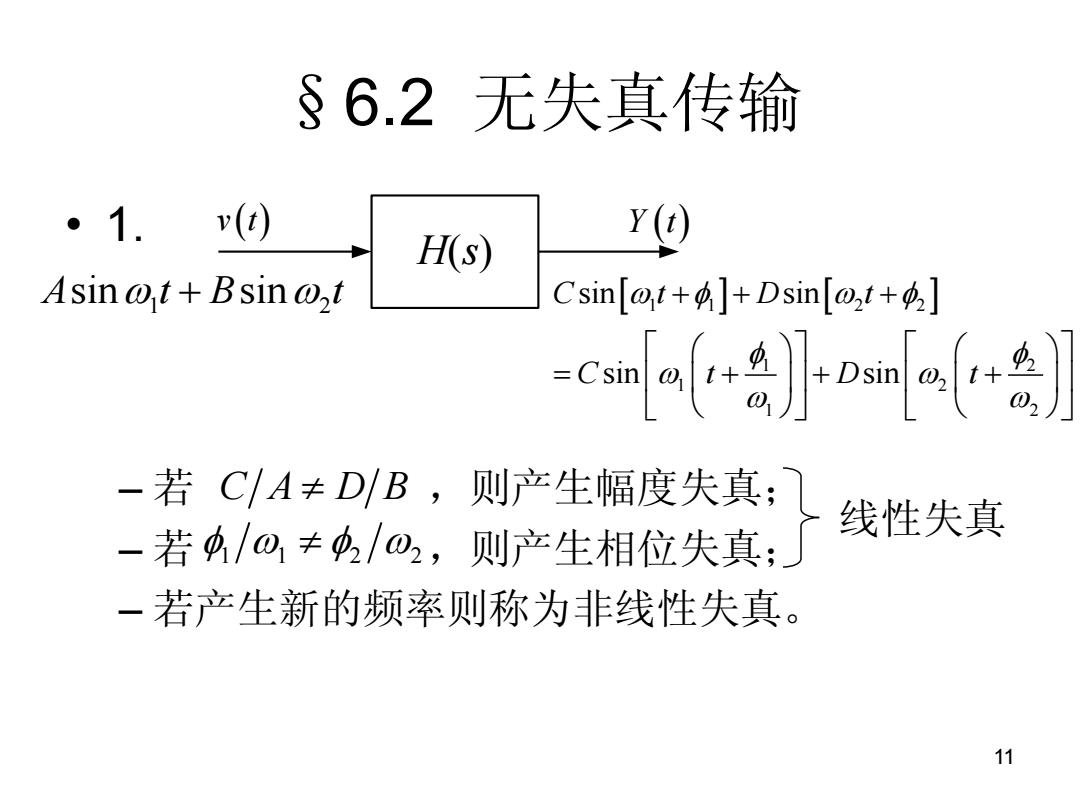
§6.2无失真传输 。1. v() H(s Y() Asin @t+Bsin@,t Csin[@t+]+Dsin[@t+] -&） -若CA≠D/B,则产生幅度失真； 线性失真 -若4/0，≠42/02，则产生相位失真； 一若产生新的频率则称为非线性失真。 11

11 §6.2 无失真传输 • 1. – 若 ，则产生幅度失真； – 若 ，则产生相位失真； – 若产生新的频率则称为非线性失真。 H(s) v t  Y t  1 2 A t B t sin sin     1 1 2 2    1 2 1 2 1 2 sin sin sin sin C t D t C t D t                                          C A D B      1 1 2 2  线性失真