I 4.最小项的编号: 把与最小项对应的变量取值当成二进制数,与之 相应的十进制数,就是该最小项的编号,用m:表示。 对应规律:原变量台1 反变量台0 ABC ABC ABC ABC ABC ABC ABC ABC 000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 o mi m2 3 ms ms m6 m
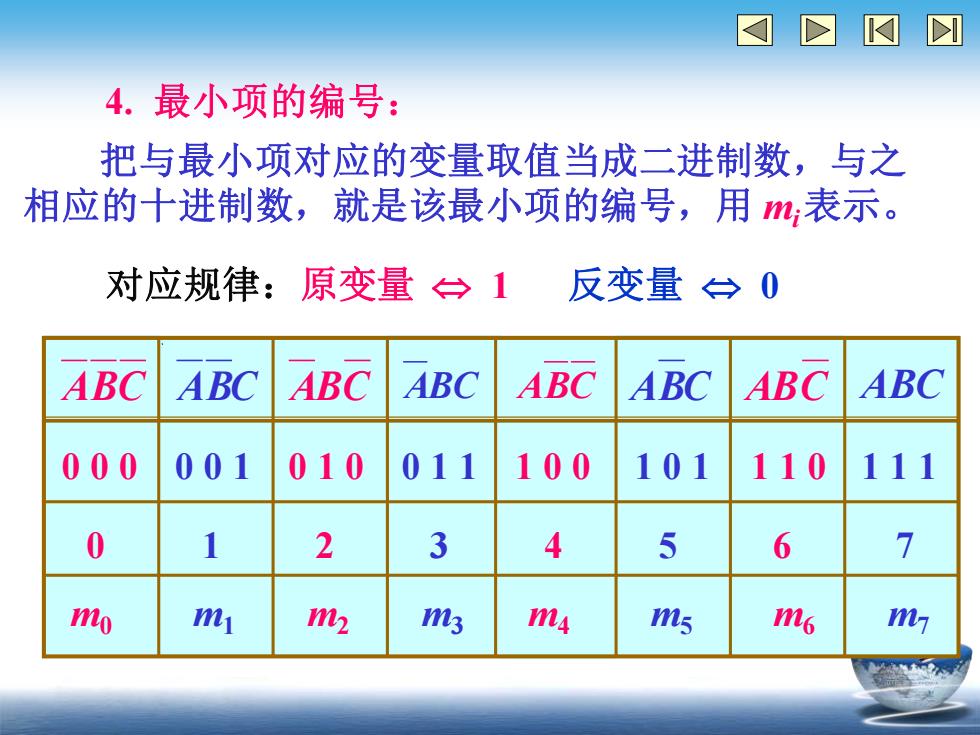
4. 最小项的编号: 把与最小项对应的变量取值当成二进制数,与之 相应的十进制数,就是该最小项的编号,用 mi 表示。 对应规律:原变量 1 反变量 0 ABC ABC ABC ABC ABC ABC ABC ABC 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 2 3 4 5 6 7 m0 m1 m2 m3 m4 m5 m6 m7

[例]写出下列函数的标准与或式: Y=AB+AD+BC=(A+B)(A+D)(B+C) =(A+BD)(B+C)=AB+AC+BCD =AB(C+C)+AC(B+B)+BCD(A+A) =ABC+ABC+ABC+ABC D+ABC D -ABCD+ABCD+ABCD+ABC D 与前面m m m6 ms ms 相重 +ABCD+ABCD+ABCD m mo ms =m +m+ms +m+m+mo+ms =∑m(0,1,4,5,6,7,8)
[例] 写出下列函数的标准与或式: Y = AB+ AD + BC = (A+ B) (A+ D) (B + C) = (A+ B D) (B + C) = AB+ AC + BC D = AB(C + C) + AC(B + B) + B C D(A+ A) = ABC + ABC + ABC + ABC D+ ABC D A B CD A B C D AB C D A B C D ABCD AB C D ABCD ABC D + + + + = + + + m7 m6 m5 m4 m1 m0 m8 = m7 +m6 +m5 + m4 + m1 + m0 + m8 = ( 0 , 1, 4 , 5 , 6 , 7 , 8 ) m m0 与前面m0 相重

二、逻辑函数的最简表达式 1.最简与或式:乘积项的个数最少,每个乘积项中相 乘的变量个数也最少的与或表达式。 例如:Y=AB+AC+BC+BCD =AB+AC+BC=AB+AC 2.最简与非- 非号最少,每个非号下面相乘的变量 与非式: 个数也最少的与非-与非式。 [例1.2.3]写出下列函数的最简与非-与非式: Y=AB+AC [解]Y=AB+AC=AB·AC
二、逻辑函数的最简表达式 Y = AB+ AC + BC + BCD 1. 最简与或式: 乘积项的个数最少,每个乘积项中相 乘的变量个数也最少的与或表达式。 例如: = AB+ AC + BC = AB+ AC 2. 最简与非 – 与非式: 非号最少,每个非号下面相乘的变量 个数也最少的与非 - 与非式。 [例 1. 2. 3] 写出下列函数的最简与非 - 与非式: Y = AB+ AC [解] Y = AB+ AC = AB AC

ID☑I 3.最简或与式:括号个数最少,每个括号中相加的变 量的个数也最少的或与式。 [例1.2.4]写出下列函数的最简与或式: Y=AB+AC [解]Y=AB+AC Y=AB+AC AB.AC =(A+B)(A+C) 4.最简或非一非号个数最少,非号下面相加的变量 或非式: 个数也最少的或非-或非式。 [例1.2.5] 写出下列函数的最简或非一或非式: Y=AB+AC [解] Y=(A+B)(A+C) =A+B+A+(
= (A+ B) (A+ C) 3. 最简或与式: 括号个数最少,每个括号中相加的变 量的个数也最少的或与式。 [例 1. 2. 4] 写出下列函数的最简与或式: Y = AB+ AC [解] Y = AB+ AC Y = AB + AC = AB AC 4. 最简或非 – 或非式: 非号个数最少,非号下面相加的变量 个数也最少的或非 – 或非式。 [例 1. 2. 5] 写出下列函数的最简或非 – 或非式: Y = AB+ AC [解] Y = (A+ B) (A+ C) = A+ B + A+ C

✉D冈I 5.最简与或非式:非号下面相加的乘积项的个数最少, 每个乘积项中相乘的变量个数也最 少的与或非式。 [例1.2.6]写出下列函数的最简与或非式: Y=AB+AC [解]已知Y=A+B+A+C=AB+AC 结论: 只要得到函数的最简与或式,再用摩根定 理进行适当变换,就可以获得其它几种类 型的最简式。而最简与或式一般需要经过 化简才能求得
5. 最简与或非式: 非号下面相加的乘积项的个数最少, 每个乘积项中相乘的变量个数也最 少的与或非式。 [例 1. 2. 6] 写出下列函数的最简与或非式: Y = AB+ AC [解] Y = A+ B + A+ C = AB + AC 结论: 只要得到函数的最简与或式,再用摩根定 理进行适当变换,就可以获得其它几种类 型的最简式。而最简与或式一般需要经过 化简才能求得。 已知