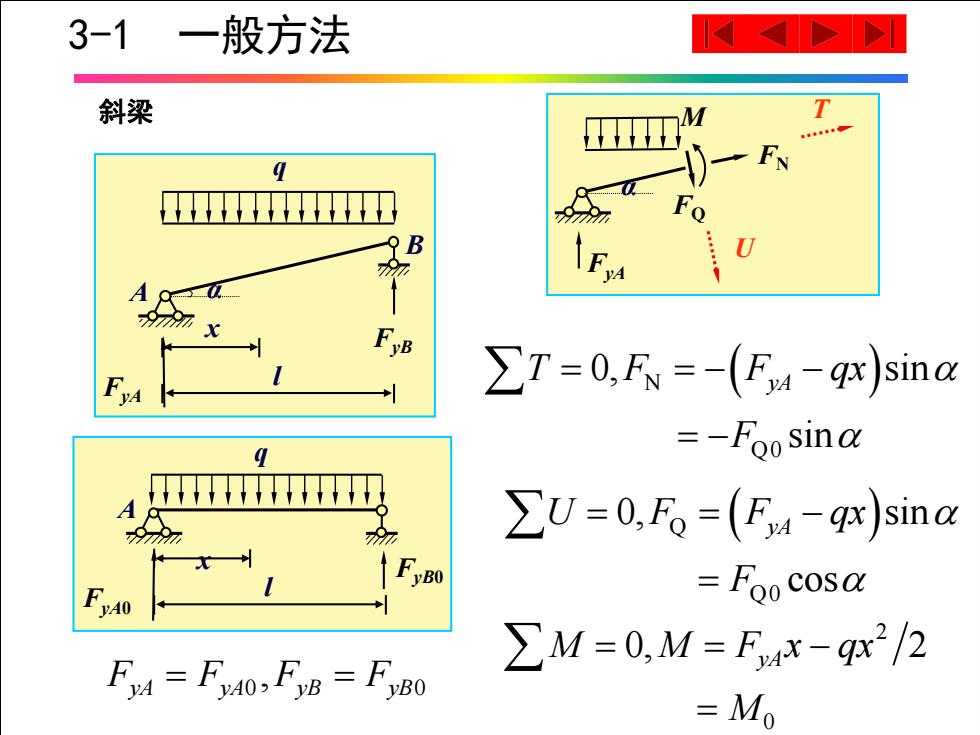
3-1 一般方法 斜梁 FN 997 B A ∑T=0,F=-(F4-9 w)sina =-Foo sina ∑U=0,F。=(F,4-9g)sina Fgo cosa ∑M=0,M=F,Mx-gx2/2 =M0
l x q FyAA B FyB l x q FyA 0A FyB 0 N ( ) Q 0 0, sin sin = = − − = − T F F qx yA F 0 0 = = , F F F F yA yA yB yB Q ( ) Q 0 0, sin cos = = − = U F F qx yA F 2 0 = = − 0, 2 = M M F x qx yA M 斜梁 α MFQ FN FyA T U α 3 -1 一般方法
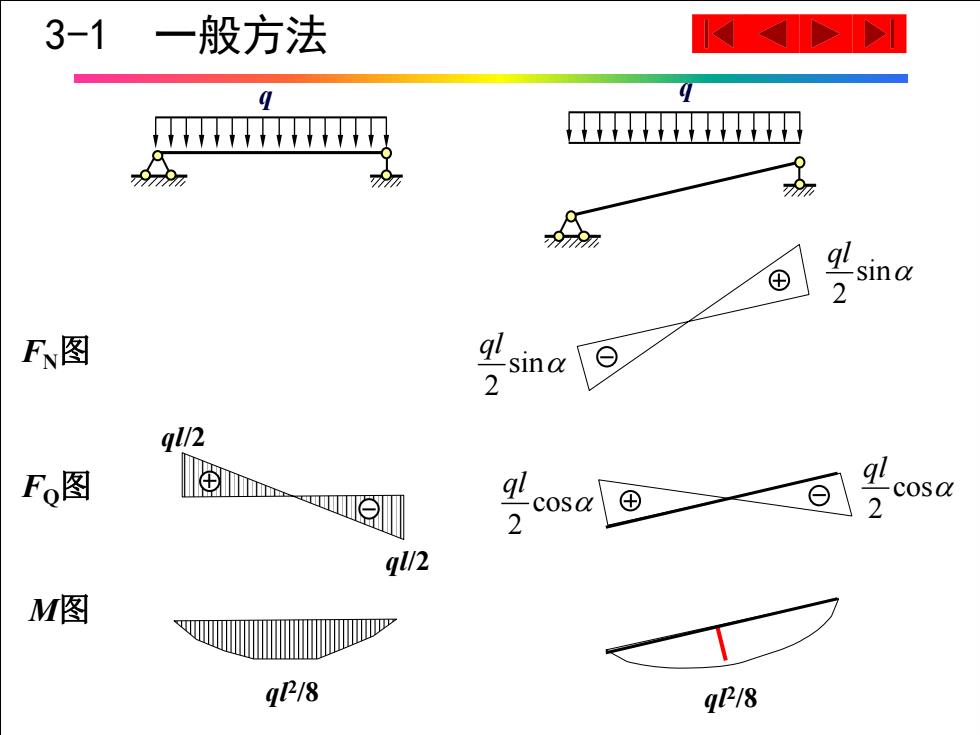
3-1 一般方法 ⊕ qlsina 2 F图 -sina 2 l/2 Fo图 ⊕ cosa cosa 2 2 ql2 M图 严 4/8 q18
q ql2 /8 sin 2 ql sin 2 ql cos 2 ql cos 2 ql M图 FN图 FQ图 q ql2 /8 ql/2 ql/2 3-1 一般方法
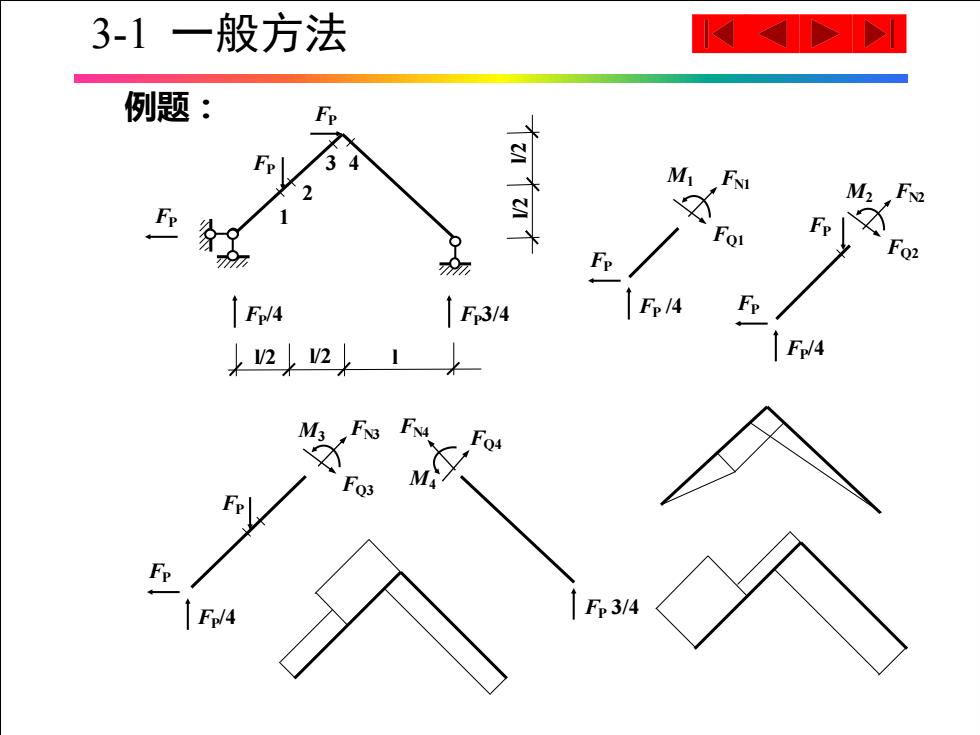
3-1一般方法 例题: M FNI Fo F/4 F3/4 Fp/4 k22 F/4 Fo 4 F3/4
FP FP/4 FN2 FQ2 FP M2 FP FP /4 FN1 FQ1 M1 例题: FP FP/4 FN3 FQ3 FP M3 FN4 FQ4 M4 FP 3/4 l/2 FP l/2 l FP 1 2 3 4 FP3/4 FP FP/4 l/2 l/2 3-1 一般方法

3-2 多跨静定梁 ✉D> 只承受竖向荷载和弯矩 Fpi 99 ,BC B ■作用在两部分交接处的集 基本部分:能独立承受外载。 中力,由基本部分来承担。 附属部分:不能独立承受外载。 先算附属部分, 后算基本部分。 ■基本部分上的荷载不影响附 属部分受力。 3-2多跨静定梁 ■附属部分上的荷载影响基本 部分受力
3-2 多跨静定梁 3-2 多跨静定梁 只承受竖向荷载和弯矩 先算附属部分, 后算基本部分。 FP2 FP1 A B C FP2 FP1 A B FP A B C 基本部分:能独立承受外载。 附属部分:不能独立承受外载。 ■基本部分上的荷载不影响附 属部分受力。 ■附属部分上的荷载影响基本 部分受力。 ■作用在两部分交接处的集 中力,由基本部分来承担
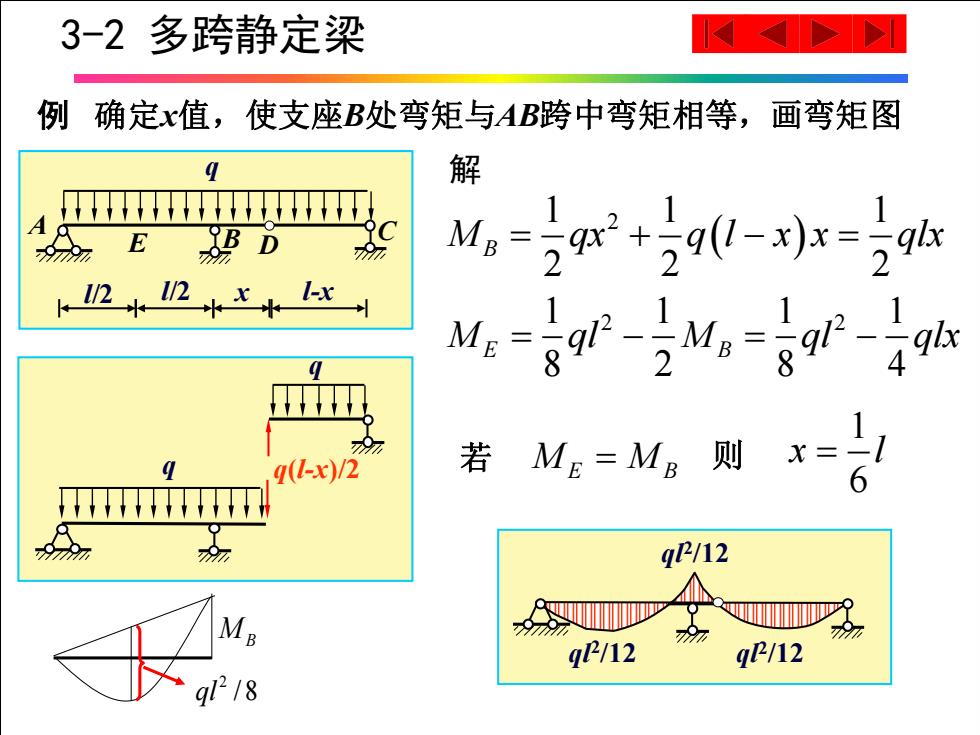
3-2多跨静定梁 例确定x值,使支座B处弯矩与AB跨中弯矩相等,画弯矩图 解 1 E 992 D ME= MB- 9 q(-x)/2 若ME=Mg则x= 17777777 9 q12 MB q112 qP/12 gl218
q q q(l-x)/2 q l/2 l/2 x l-x A B C E D 解 ( ) 1 1 1 2 2 2 2 M qx q l x x qlx B = + − = 1 1 1 1 2 2 8 2 8 4 M ql M ql qlx E B = − = − 若 M M E B = 则 1 6 x l = / 8 2 qlMB 例 确定x值,使支座B处弯矩与AB跨中弯矩相等,画弯矩图 ql2 /12 ql2 /12 ql2 /12 3-2 多跨静定梁