
Advanced Algorithms Balls into Bins 尹一通Nanjing University,202Fall
尹⼀通 Nanjing University, 202 Fall Advanced Algorithms Balls into Bins
Balls into Bins n balls uniform independent m bins 44↓4↓444 random function f:[n][m] birthday,coupon collector,occupancy
Balls into Bins n balls m bins uniform & independent birthday, coupon collector, occupancy, ... random function f : [n] → [m]
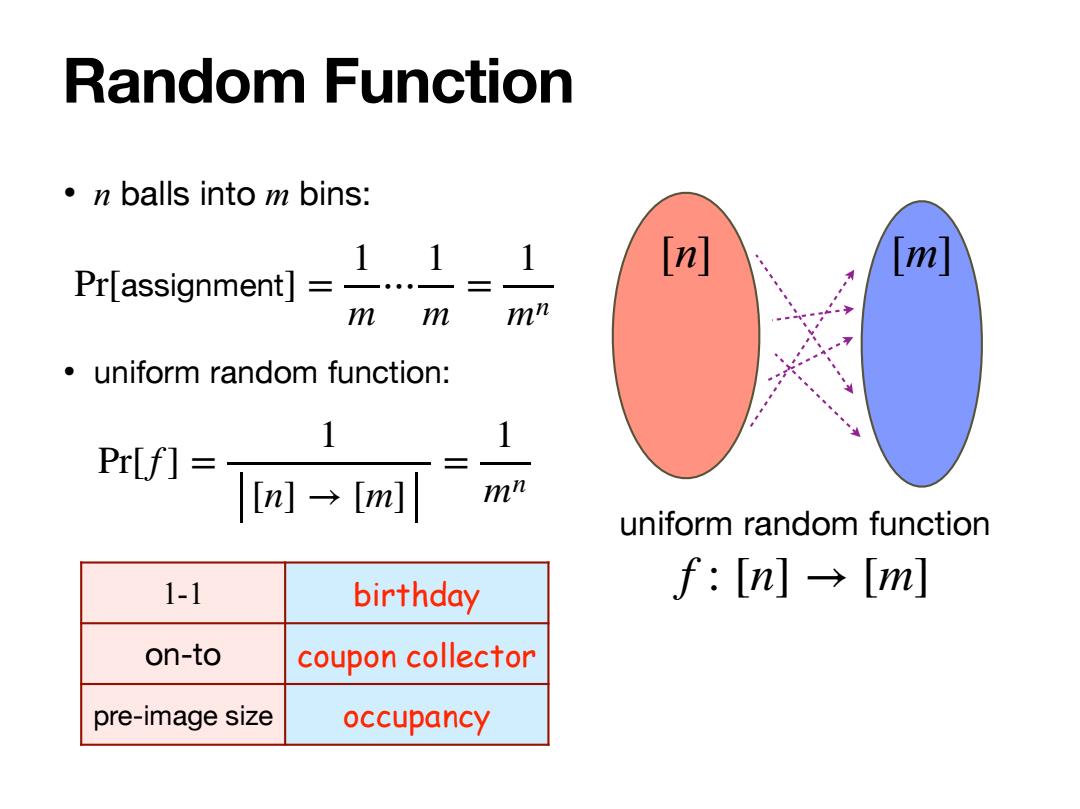
Random Function ·n balls into m bins: Pr(assignment]=1. 1 [m] [m] mm mn uniform random function: 1 1 Pr[f]= [m→m] mn uniform random function 1-1 birthday f:[n]→[m] on-to coupon collector pre-image size occupancy
Random Function • n balls into m bins: • uniform random function: Pr[assignment] = 1 m ⋯ 1 m = 1 mn Pr[f ] = 1 [n] → [m] = 1 mn [n] [m] uniform random function f : [n] → [m] 1-1 birthday on-to coupon collector pre-image size occupancy

Birthday Paradox Paradox: (i)a statement that leads to a contradiction; (ii)a situation which defies intuition. In a class of m>57 students,with >99%probability, there are two students with the same birthday. Assumption:birthdays are uniformly independently distributed. n balls are thrown into m bins: event each bin receives 1 balls
Birthday Paradox Paradox: (i) a statement that leads to a contradiction; (ii) a situation which defies intuition. In a class of m>57 students, with >99% probability, there are two students with the same birthday. Assumption: birthdays are uniformly & independently distributed. n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls

Birthday Paradox n balls are thrown into m bins: event each bin receives 1 balls m与[ m(m-1)…(m-n+1) Pr[8]= [n→m mn i(-)
Birthday Paradox Pr[ℰ] = [n] 1−1 [m] [n] → [m] = m(m − 1)⋯(m − n + 1) mn = n−1 ∏ i=0 (1 − i m ) n balls are thrown into m bins: event ℰ: each bin receives ≤ 1 balls