
2、虚拟变量模型 ·同时含有一般解释变量与虚拟变量的模型称为 虚拟变量模型或者方差分析(analysis-of variance:ANOVA)模型。 。1 例如,一个以性别为虚拟变量考察企业职工薪 金的模型: Y,=B。+BX,+B2D,+4 其中:Y为企业职工的薪金;X为工龄;D=1, 若是男性,D=0,若是女性
2、虚拟变量模型 • 同时含有一般解释变量与虚拟变量的模型称为 虚拟变量模型或者方差分析(analysis-of variance: ANOVA)模型。 • 例如,一个以性别为虚拟变量考察企业职工薪 金的模型: Yi = 0 + 1 Xi + 2 Di + i 其中:Yi为企业职工的薪金;Xi为工龄; Di=1, 若是男性,Di=0,若是女性

二、虚拟变量的引入
二、虚拟变量的引入

1、加法方式 ● 虚拟变量作为解释变量引入模型有两种基本方 式:加法方式和乘法方式。 ·上述企业职工薪金模型中性别虚拟变量的引入 采取了加法方式。 在该模型中,如果仍假定E(μ)=0,则企业男、 女职工的平均薪金为: E(Y,|X,D,=1)=(B。+B2)+BX, EY,IX,D,=0)=B。+BX
1、加法方式 • 虚拟变量作为解释变量引入模型有两种基本方 式:加法方式和乘法方式。 • 上述企业职工薪金模型中性别虚拟变量的引入 采取了加法方式。 在该模型中,如果仍假定E(i )=0,则企业男、 女职工的平均薪金为: E Yi Xi Di 0 1 Xi ( | , = 0) = + E Yi Xi Di 0 2 1 Xi ( | , =1) = ( + ) +
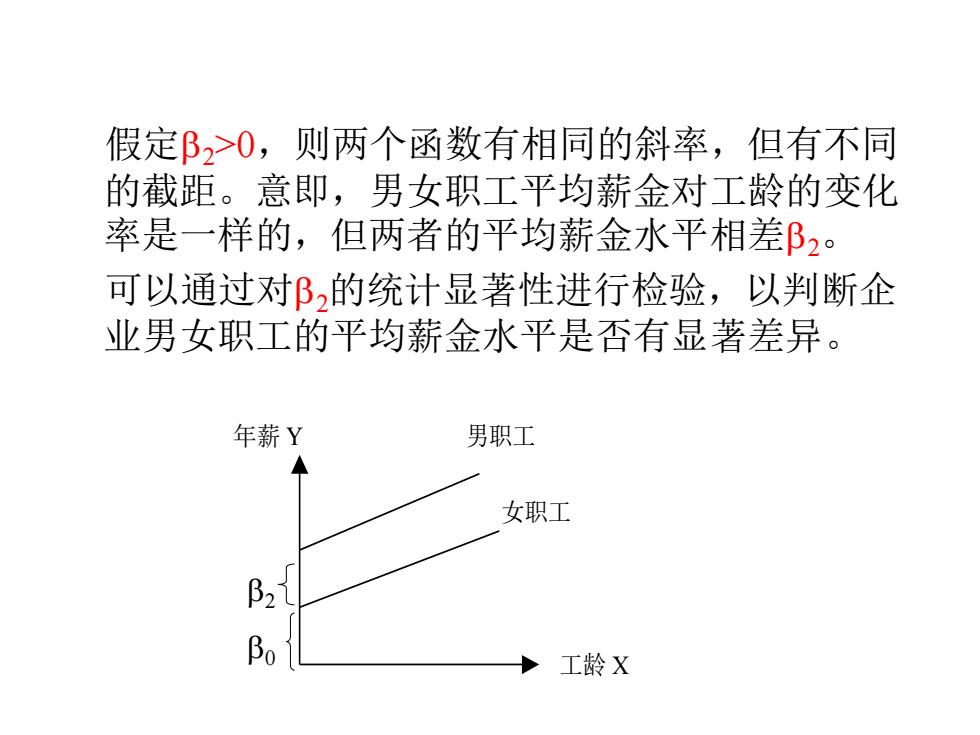
假定β2>0,则两个函数有相同的斜率,但有不同 的截距。意即,男女职工平均薪金对工龄的变化 率是一样的,但两者的平均薪金水平相差β2。 可以通过对B,的统计显著性进行检验,以判断企 业男女职工的平均薪金水平是否有显著差异。 年薪Y 男职工 女职工 B21 Bo 工龄X
假定2>0,则两个函数有相同的斜率,但有不同 的截距。意即,男女职工平均薪金对工龄的变化 率是一样的,但两者的平均薪金水平相差2。 可以通过对2的统计显著性进行检验,以判断企 业男女职工的平均薪金水平是否有显著差异。 年薪 Y 男职工 女职工 工龄 X 0 2
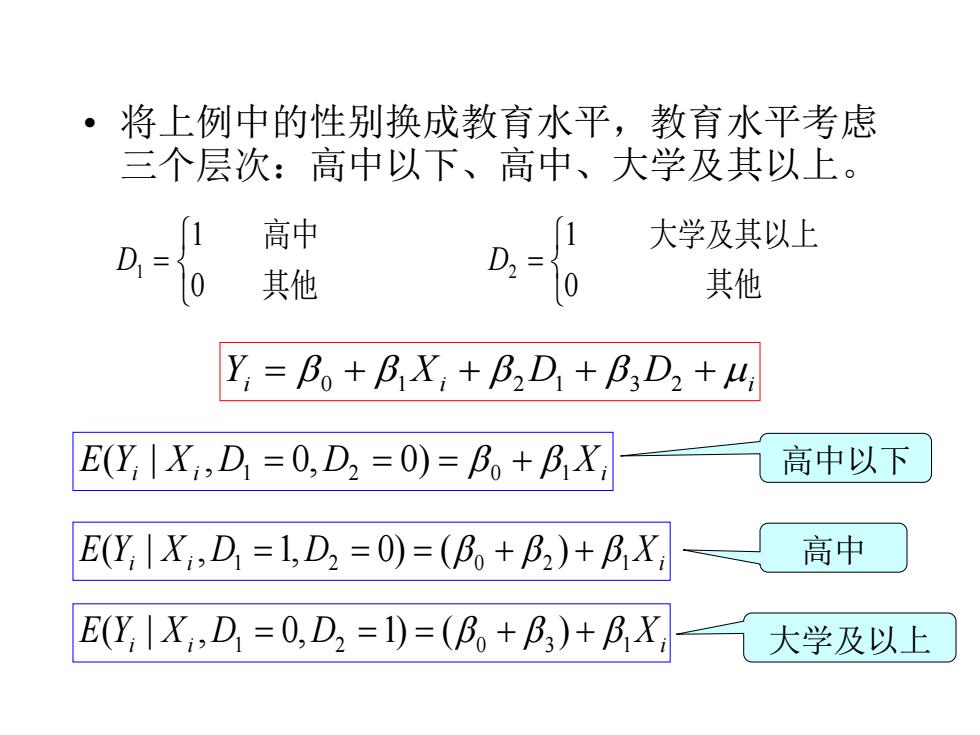
·将上例中的性别换成教育水平,教育水平考虑 三个层次:高中以下、高中、大学及其以上。 D.0 高中 1 大学及其以上 其他 D2= 0 其他 Y,=B。+BX,+B2D,+B3D2+4 E(Y,IX,D1=0,D2=0)=B。+BX 高中以下 E(Y,|X,D=1,D2=0)=(B+B)+BX 高中 E(Y,|X,D=0,D2=1)=(B。+B3)+BX: 大学及以上
• 将上例中的性别换成教育水平,教育水平考虑 三个层次:高中以下、高中、大学及其以上。 = 0 1 D1 其他 高中 = 0 1 D2 其他 大学及其以上 Yi = 0 + 1 Xi + 2 D1 + 3 D2 + i E Yi Xi D1 D2 0 1 Xi ( | , = 0, = 0) = + E Yi Xi D1 D2 0 2 1 Xi ( | , =1, = 0) = ( + ) + E Yi Xi D1 D2 0 3 1 Xi ( | , = 0, =1) = ( + ) + 高中以下 高中 大学及以上