《电工技术》课程教学课件（课件讲稿）第2章 电路的分析方法

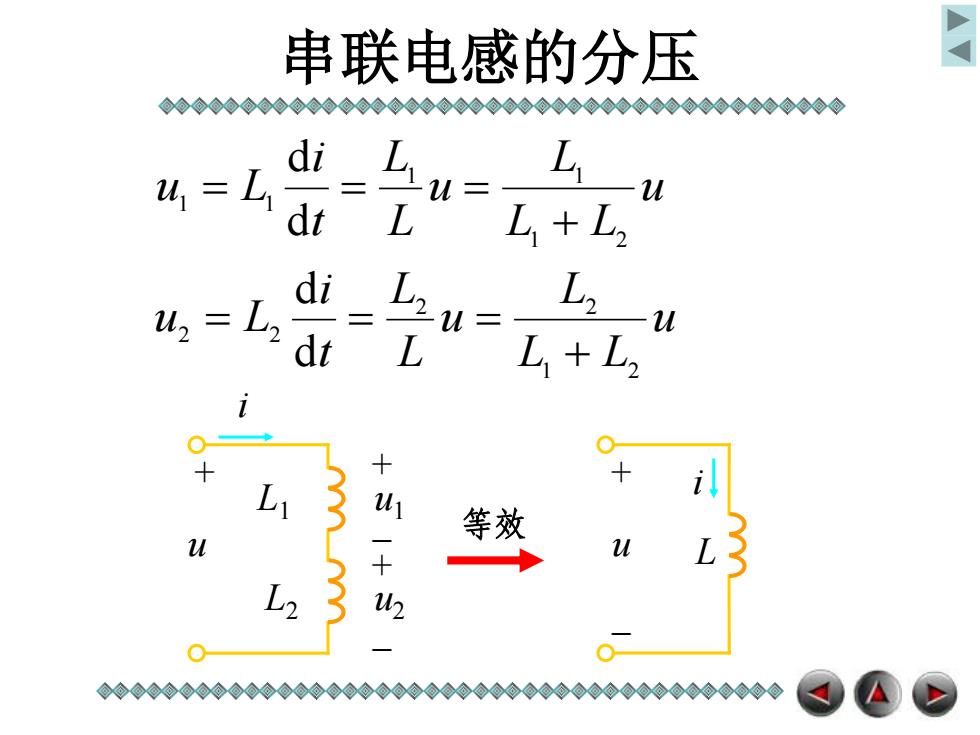
串联电感的分压 ⊙0⊙◆0⊙⊙◇⊙0◇◆0◇@0⊙⊙0◇0@00◇@0⊙⊙0⊙◆0⊙◇0◇00@ di 4=L dt L L+L di 42=L2 L dt 2u L,+L2 L uj 等效 u2 ◆⊙@00◇◇⊙◇0◆◆⊙◆00◇O◇◇◆◇◆◆⊙⊙@0⊙⊙◇⊙⊙⊙◆0⊙◆0◇◆

串联电感的分压 u L L L u L L t i u L 1 2 1 1 1 1 d d     u L L L u L L t i u L 1 2 2 2 2 2 d d     u1 u L2 L1 u2 + + + - - i i u + - L 等效

4、电感的并联 等效 =i-2ud-.6a = L+L

４、电感的并联   t u ξ ξ L i ( )d 1 1 1 u + - L1 L2 i2 i1 i u + - L 等效   t u ξ ξ L i ( )d 1 2 2             t u ξ ξ L L i i i ( )d 1 1 1 1 1 2   t u ξ ξ L ( )d 1 1 2 1 2 1 1 1 1 1 L L L L L L L           

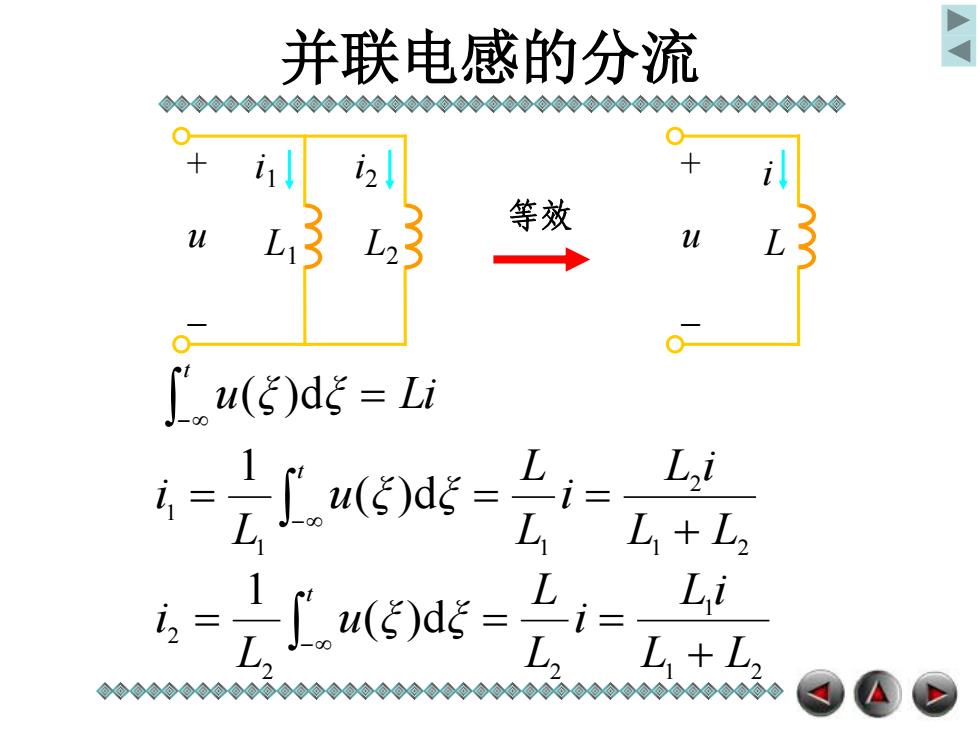
并联电感的分流 等效 u(e)de Li i-2打63d越- i L,i L +Lz 4=了(5)d= Li L+L

并联电感的分流 u ξ ξ Li t  ( )d  1 2 2 1 1 1 ( )d 1 L L L i i L L u ξ ξ L i t       1 2 1 2 2 2 ( )d 1 L L L i i L L u ξ ξ L i t       u + - L1 L2 i2 i1 i u + - L 等效

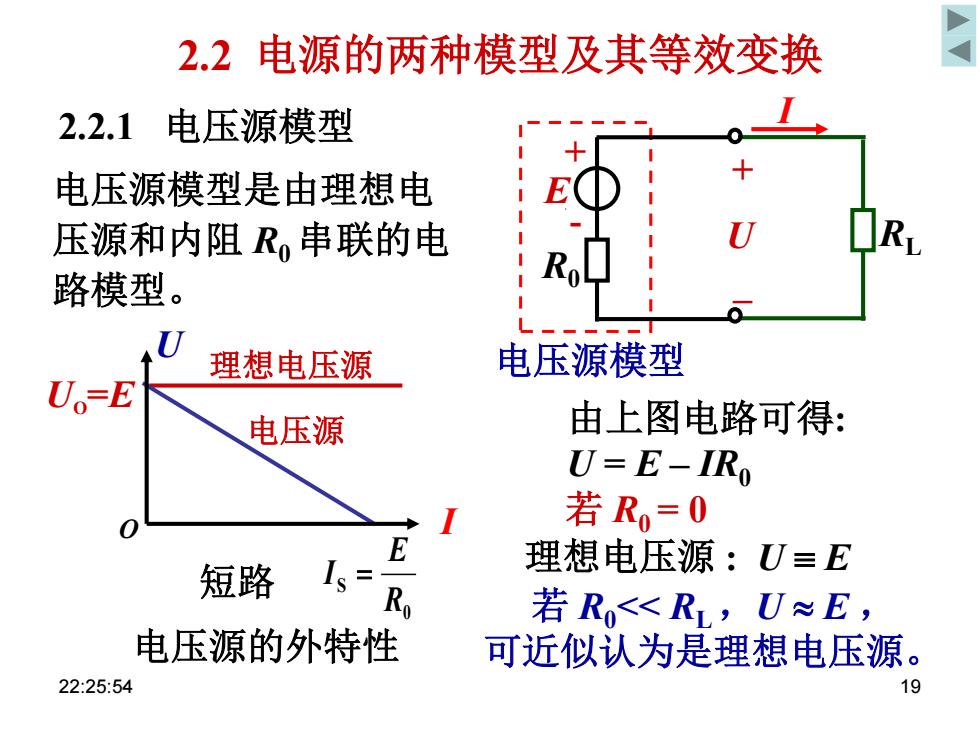
2.2电源的两种模型及其等效变换 2.2.1电压源模型 电压源模型是由理想电 压源和内阻R,串联的电 路模型。 U 理想电压源 电压源模型 U。E 电压源 由上图电路可得： U=E-IRo 若R=0 E 短路 Is= 理想电压源：U≡E 若R<RL,UNE, 电压源的外特性 可近似认为是理想电压源。 22:25:54 19

2.2 电源的两种模型及其等效变换 2.2.1 电压源模型 电压源模型 由上图电路可得: U = E – IR0 若 R0 = 0 理想电压源 : U  E UO =E 电压源的外特性 I U I RL R0 + - E U + – 电压源模型是由理想电 压源和内阻 R0 串联的电 路模型。 0 S R E I  若 R0<< RL ，U  E ， 可近似认为是理想电压源。 理想电压源 O 电压源 短路 22:25:54 19

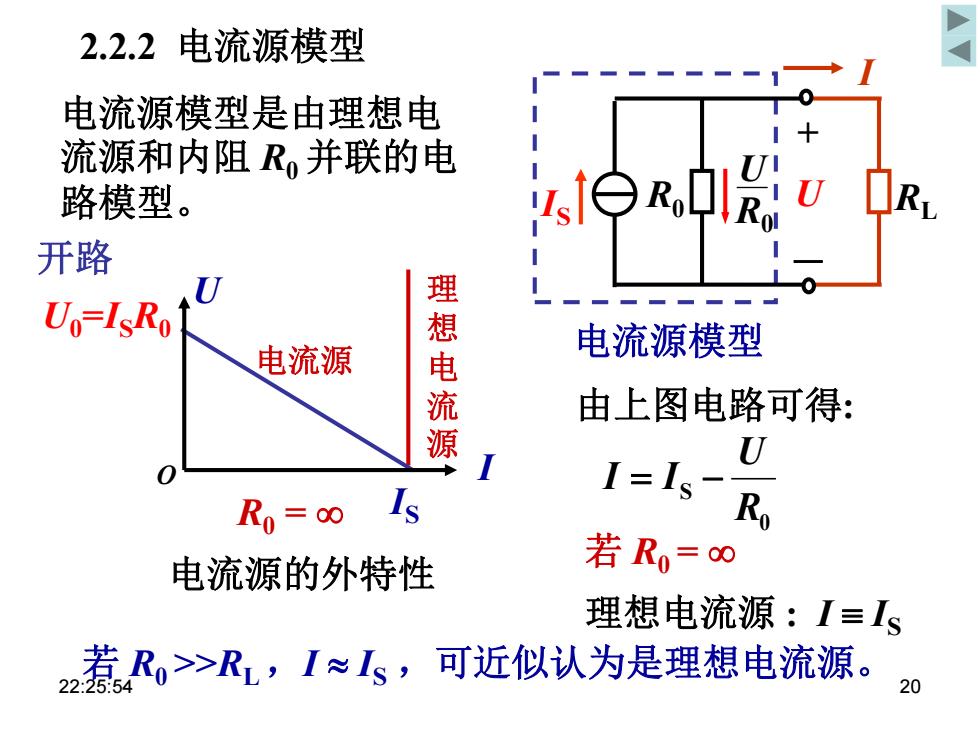
2.2.2电流源模型 电流源模型是由理想电 流源和内阻R,并联的电 路模型。 白R,中I U R 开路 Uo=IsRo 电流源 电 电流源模型 由上图电路可得： 源 U R0=0 Is 1=1 电流源的外特性 若R0=∞ 理想电流源：I≡s 2惹R>R,1≈，可近似认为是理想电流源。 20

2.2.2 电流源模型 0 S R U I  I  I RL U0 =ISR0 电流源的外特性 I U 理 想 电 流 源 O IS 电流源模型是由理想电 流源和内阻 R0 并联的电 路模型。 由上图电路可得: 若 R0 =  理想电流源 : I  IS 若 R0 >>RL ，I  IS ，可近似认为是理想电流源。 电流源 电流源模型 R0 U R0 U IS + 开路 － R0 =  22:25:54 20