描迷傲见的体运动规律的需朱呼唤物程学新概念的延生! 人们对物质和能量的认识是否只看到了硬币的一面? 波粒二象性是解决原子结构问题的“总开关 1,2.2波的微粒性 。电磁波是通过空间传播的能量.可见光只不过是电磁波的一种, Approximate frequencies.! 1024 102 1020 101 X-may 10-16 10-4 10-2 10- Approximate wavelengths.m 450 500 550 650 The electromagnetic spectrum 电磁波在有些情况下表现出连续波的性质,另一些情况下则更像 单个微粒的集合体,后一种性质叫作波的微粒性。 上页 下页 节首 节尾
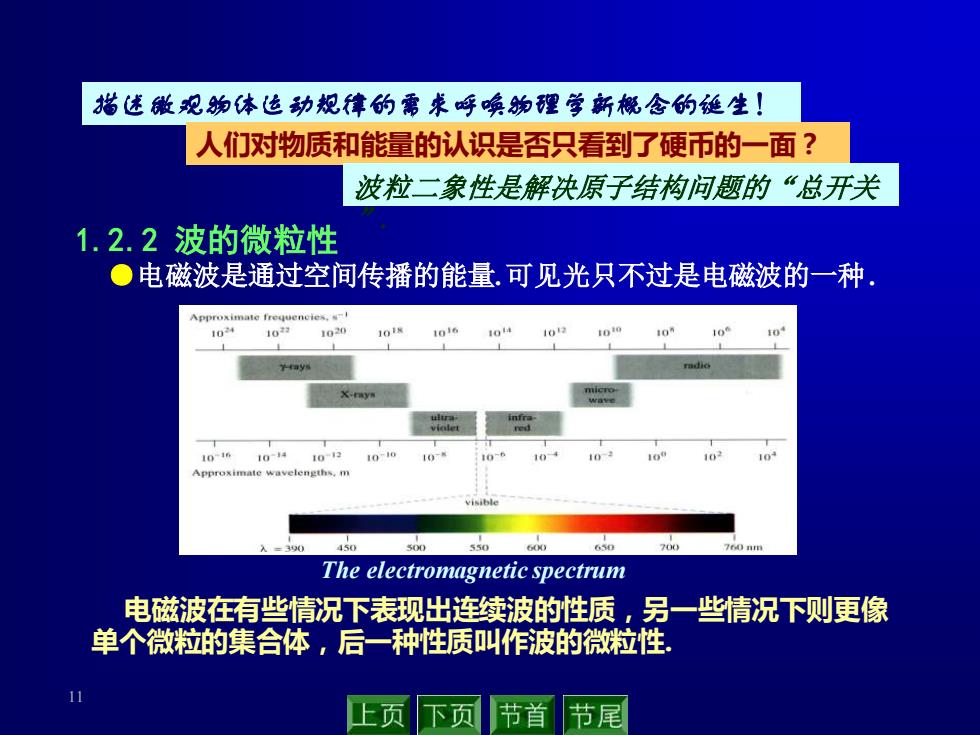
11 1.2.2 波的微粒性 描述微观物体运动规律的需求呼唤物理学新概念的诞生! 人们对物质和能量的认识是否只看到了硬币的一面? 波粒二象性是解决原子结构问题的“总开关 ”. ●电磁波是通过空间传播的能量. 可见光只不过是电磁波的一种. The electromagnetic spectrum 电磁波在有些情况下表现出连续波的性质,另一些情况下则更像 单个微粒的集合体,后一种性质叫作波的微粒性

Plank公式 1900年,普朗克Plank M0提出了表达光的能量(E)与频率(v) 关系的方程,即著名的普朗克方程:E=hy 式中的h叫普朗克常量(Planck constant,)其值为6.626×1034Js. 普朗克认为,物体只能按的整数倍(例如1,2,3等)一份一份地 吸收或释出光能,而不可能是0.5,1.6,2.3等任何非整数倍.这就是 所谓的能量量子化概念. 普朗克提出了当时物理学界一种全新的概念,但它只涉及光作 用于物体时能量的传递过程(即吸收或释出). 比 拟 地面吸收太阳能 地面接收降水 ★以一个个光量子“v”(不能是半个“加”)完成.★一似个雨滴(不能是半个雨滴完成) ★可见光由不同颜率的光组成,“m”值有大有小·★“雨滴”有大有小 ★黄光的y值相对较大,“m”较大,光量子的能量大·★相当于较大的“雨滴”,落至地面时的动能较大 ★红光的”值相对较小,“m”较小,光量子的能量较小★相当于较小的“雨滴”,落至地面时的动能较小 上页 下页 节首 节尾
12 1900年, 普朗克(Plank M) 提出了表达光的能量(E)与频率(ν) 关系的方程, 即著名的普朗克方程:E= h ν 式中的h叫普朗克常量(Planck constant),其值为6.626×10-34 J·s. 普朗克认为, 物体只能按hν的整数倍(例如1, 2, 3等)一份一份地 吸收或释出光能, 而不可能是0.5, 1.6, 2.3等任何非整数倍.这就是 所谓的能量量子化概念. 普朗克提出了当时物理学界一种全新的概念, 但它只涉及光作 用于物体时能量的传递过程(即吸收或释出). ● Plank 公式 地面吸收太阳能 地面接收降水 ★以一个个 光量子 “hν ”(不能是半个 “hν ”)完成. ★可见光由不同频率的光组成 , “hν ”值有大有小 . ★黄光的 ν 值相对较大 ,“hν ”较大 ,光量子的能量大 . ★红光的 ν 值相对较小 ,“hν ”较小 , 光量子的能量较小 . ★ 一个个雨滴 以 ( 不能是半个雨滴 完成) ★“雨滴”有大有小 ★相当于较大的 “雨滴”,落至地面时的动能较大 ★相当于较小的 “雨滴”,落至地面时的动能较小 比 拟
●光电效应 1905年,爱因斯坦(Einstein A)成功地解释 @@ 了光电效应(photoelectric effect),将能量量子 (hy 化概念扩展到光本身.对某一特定金属而言,不 是任何频率的光都能使其发射光电子.每种金 属都有一个特征的最小频率(叫临界频率),低 于这一频率的光线不论其强度多大和照射时 h 0。e”00百 间多长,都不能导致光电效应 The photoelectric effect 爱因斯坦认为,入射光本身的能量也按普朗克方程量子化,并将 这一份份数值为1的能量叫光子(photons),一束光线就是一束光子 流。频率一定的光子其能量都相同,光的强弱只表明光子的多少, 而与每个光子的能量无关 爱因斯坦对光电效应的成功解释最终使光的微粒性为人们所接受 。 以波的微粒性概念为基础的一门学科叫量子力学(quantum mechanics). 3 节首 节尾
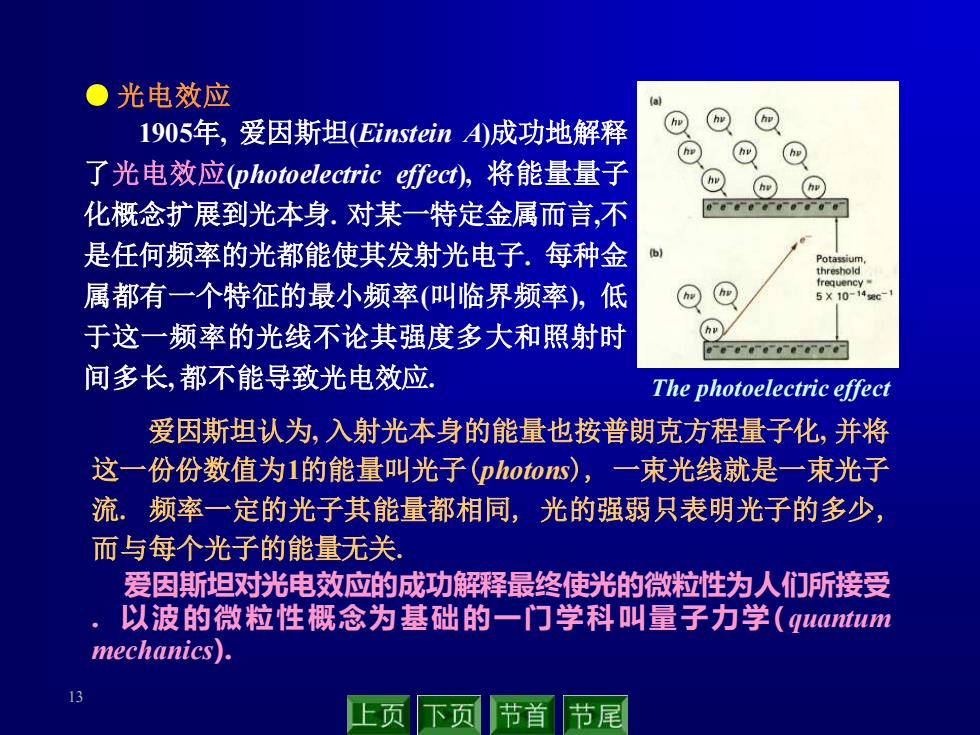
13 The photoelectric effect 爱因斯坦认为, 入射光本身的能量也按普朗克方程量子化, 并将 这一份份数值为1的能量叫光子(photons), 一束光线就是一束光子 流. 频率一定的光子其能量都相同, 光的强弱只表明光子的多少, 而与每个光子的能量无关. 爱因斯坦对光电效应的成功解释最终使光的微粒性为人们所接受 . 以波的微粒性概念为基础的一门学科叫量子力学( quantum mechanics). ● 光电效应 1905年, 爱因斯坦(Einstein A)成功地解释 了光电效应(photoelectric effect), 将能量量子 化概念扩展到光本身. 对某一特定金属而言,不 是任何频率的光都能使其发射光电子. 每种金 属都有一个特征的最小频率(叫临界频率), 低 于这一频率的光线不论其强度多大和照射时 间多长,都不能导致光电效应

ue 钾的临界频率=5.0×104s1,试计算具有这种 频率的一个光子的能量.对红光和黄光进行 类似的计算,解释金属钾在黄光作用下产生光电 效应而在红光作用下却不能, 将相关频率值代入普朗克公式: E(具有临界频率的一个光子)=6.626×1034Js×5.0X104s1=3.3×1019J E黄光一个光子)=hV=6626×1034Js×5.1×1014s1=3.4×1019J E(红光一个光子)=hv=6.626X1034Js×4.6×1014g1=3.0×101J 黄光光子的能量大于与临界频率对应的光子能量,从而引发光 电效应;红光光子的能量小于与临界频率对应的光子能量,不能引发 光电效应 上页下页 节首节尾
14 Question 1 钾的临界频率=5.0×1014 s -1 ,试计算具有这种 频率的一个光子的能量. 对红光和黄光进行 类似的 计算, 解释金属钾在黄光作用下产生光电 效应而在红光作用下却不能. 将相关频率值代入普朗克公式: E(具有临界频率的一个光子) = 6.626×10-34 J·s × 5.0×1014 s -1 = 3.3×10-19 J E(黄光一个光子) = hν= 6.626×10-34 J·s × 5.1×1014 s -1 = 3.4×10-19 J E(红光一个光子) = hν= 6.626×10-34 J·s × 4.6×1014 s -1 = 3.0×10-19 J 黄光光子的能量大于与临界频率对应的光子能量, 从而引发光 电效应; 红光光子的能量小于与临界频率对应的光子能量, 不能引发 光电效应

The experiments of particle ofelectrons The Planck The photoelectric effect equation Plank的量子论 导致了人们对波的深层次认 波的微粒性 Einstein的光子学说 识,产生了讨论波的微粒性 念为基础的学科一量子力 电子微粒性的实验 学 (quantum mechanics). 钱币的一面己被翻开! 另一面谁来翻开? 15 上页下页 节首节尾
15 另一面谁来翻开? 波的微粒性 导致了人们对波的深层次认 识,产生了讨论波的微粒性 概念为基础的学科 ⎯ 量子力 学(quantum mechanics). 钱币的一面已被翻开! Einstein 的光子学说 The photoelectric effect 电子微粒性的实验 The experiments of particle of electrons Plank 的 量子论 The Planck equation