
水人 新课 2.7应用举例(续1) 尚本 98 908772 89 90 8698 1,1,1,1)=347,363,343,346) 97 8475 87 85 88 85 88 所以每个学生各科总成绩依次为B47,363,343,346) 每个人平均分数的矩阵表示式为 98908772 87 89 908698 91 4 97 847587 86 8588 85 88 87 所以每个人平均分数依次为:87,91,86,87. 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 2.7 应用举例(续1) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 (1,1,1,1) 85 88 85 88 97 84 75 87 89 90 86 98 98 90 87 72 = (347 , 363, 343, 346). 所以每个学生各科总成绩依次为: 每个人平均分数的矩阵表示式为 85 88 85 88 97 84 75 87 89 90 86 98 98 90 87 72 4 1 1 1 1 1 . 87 86 91 87 所以每个人平均分数依次为:87,91,86,87. (347 , 363, 343, 346)

水人 新课 2.7应用举例(续2) 尚本 例2.7.2 (用可逆矩阵进行保密编译码) 在英文中有一种对消息进行保密的措施,就 是把消息中的英文字母用一个整数来表示,然后 传送这组整数.如使用代码:将26个英文字母依 次对应数字1,2,…,25,26. 若要发出信息action,此信息的编码是1,3, 20,9,15,14.用这种方法,在一个长消息中, 根据数字出现的频率,容易估计它所代表的字母, 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.7 应用举例(续2) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 例2.7.2 (用可逆矩阵进行保密编译码) 在英文中有一种对消息进行保密的措施,就 是把消息中的英文字母用一个整数来表示,然后 传送这组整数. 如使用代码:将26个英文字母依 次对应数字1,2, … ,25,26. 若要发出信息action,此信息的编码是1,3, 20,9,15,14.用这种方法,在一个长消息中, 根据数字出现的频率,容易估计它所代表的字母
水人 新课 2.7应用举例(续3) 尚本 因此容易被破译因此,利用矩阵乘法对这个 消息进一步加密 现任选一个行列式等于±的整数矩阵,如 123 A=112 0 将传出消息的编码1,3,20,9,15,14写为两个 传出的信息向量1,3,20),(9,15,14) 河套大学《线性代数》课件 第二章矩阵 快东骨司
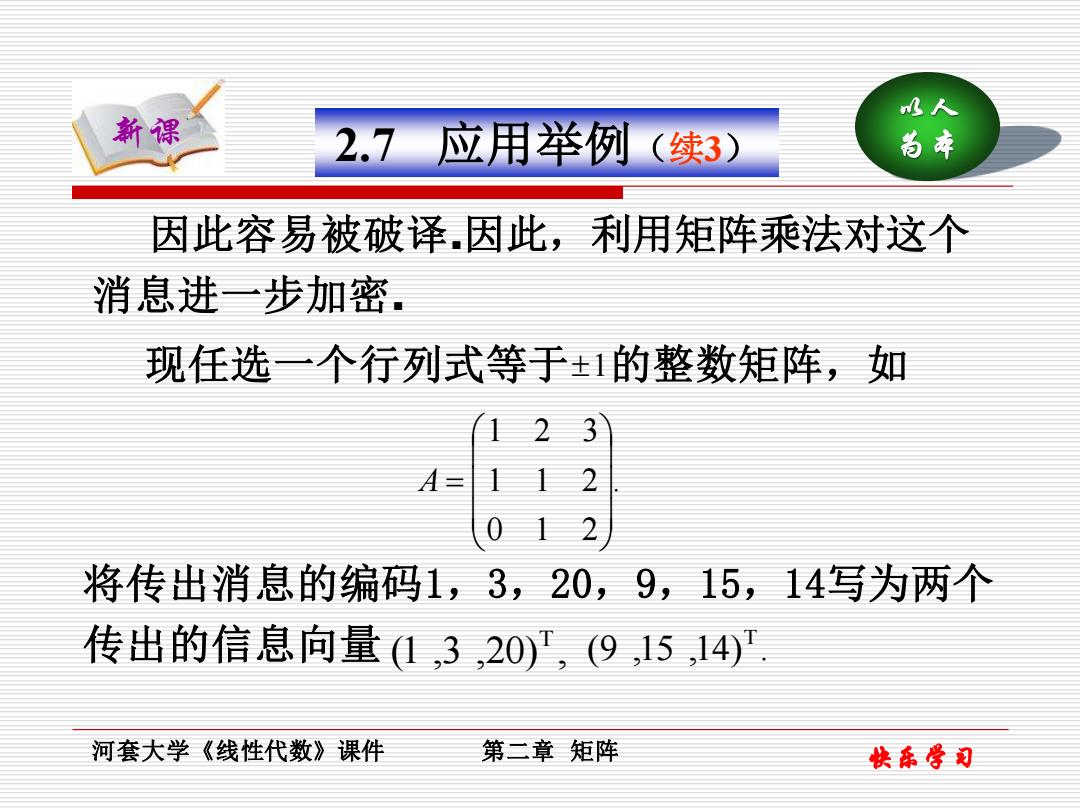
快乐学习 以人 2.7 应用举例(续3) 为本 河套大学《线性代数》课件 第二章 矩阵 新课 . 0 1 2 1 1 2 1 2 3 A = 因此容易被破译.因此,利用矩阵乘法对这个 消息进一步加密. 现任选一个行列式等于 的整数矩阵,如 将传出消息的编码1,3,20,9,15,14写为两个 传出的信息向量 (1 ,3 ,20) , T (9 ,15 ,14) . T 1