华东师范大学：《现代数值分析》课程教学课件（数值线性代数）第五讲 对称矩阵的特征值问题（5.4-5.7）

第五讲 对称特征值问题 1 Jacobi迭代方法 2 Rayleigh商迭代方法 3 对称QR迭代方法 4 分而治之法 5 对分法和反迭代 6 奇异值分解 7 扰动分析 现代数位分析（数值线性代数），潘建瑜 http://math.ecnu.edu.cn/~jypan

第五讲 对称特征值问题 1 Jacobi 迭代方法 2 Rayleigh 商迭代方法 3 对称 QR 迭代方法 4 分而治之法 5 对分法和反迭代 6 奇异值分解 7 扰动分析 现代数值分析（数值线性代数）, 潘建瑜 http://math.ecnu.edu.cn/~jypan

秦 4 分而治之法 分而治之法由Cuppen于1981年首次提出，但直到1995年才出现稳定的实现 方式，是目前计算所有特征值和特征向量的最快算法. 考虑不可约对称三对角矩阵 b1 am-1 bm-1 bm-1 am bm T= bm am+1 bm+1 bm+1 bn-1 bn-1 an http://math.ecnu.edu.cn/~jypan 18/77

4 分而治之法 分而治之法由 Cuppen 于 1981 年首次提出, 但直到 1995 年才出现稳定的实现 方式, 是目前计算 所有特征值和特征向量 的最快算法. 考虑不可约对称三对角矩阵 T =                     a1 b1 b1 . . . . . . . . . am−1 bm−1 bm−1 am bm bm am+1 bm+1 bm+1 . . . . . . . . . . . . bn−1 bn−1 an                     http://math.ecnu.edu.cn/~jypan 18/77

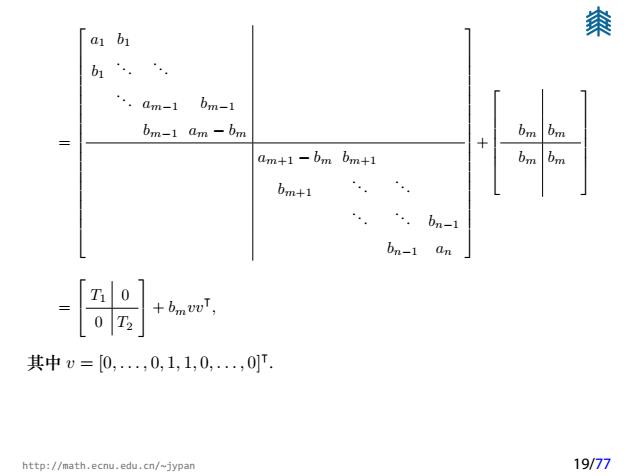
秦 b1 am-1 bm-1 bm-1 am-bm bm bm am+1-bm bm+1 bm bm bm+1 bn-1 bn-1 an 0 +bmwv, 其中v=[0.,0,1,1,0,.,0]T http://math.ecnu.edu.cn/~jypan 19/77

=                     a1 b1 b1 . . . . . . . . . am−1 bm−1 bm−1 am − bm am+1 − bm bm+1 bm+1 . . . . . . . . . . . . bn−1 bn−1 an                     +        bm bm bm bm        =   T1 0 0 T2   + bmvv ⊺ , 其中 v = [0, . . . , 0, 1, 1, 0, . . . , 0]⊺ . http://math.ecnu.edu.cn/~jypan 19/77

秦 假定T1和T2的特征值分解已经计算出来 即T=Q1△1Q1,T2=Q2A2Q2,下面考虑T的特征值分解. T 0 T QiAIQI 0 0T2 0 Q242Q5 -ed网e 其中 - Q1的最后一列 令a=bm,D=diag(A1,A2)=diag(d1,d2,.,dn),并假定d1≥d2≥…≥dn. 则T的特征值与D+auuT的特征值相同. http://math.ecnu.edu.cn/~jypan 20/77

假定 T1 和 T2 的特征值分解已经计算出来 即 T1 = Q1Λ1Q ⊺ 1 , T2 = Q2Λ2Q ⊺ 2 , 下面考虑 T 的特征值分解. T =   T1 0 0 T2   + bmvv ⊺ =   Q1Λ1Q ⊺ 1 0 0 Q2Λ2Q ⊺ 2   + bmvv ⊺ =   Q1 0 0 Q2       Λ1 0 0 Λ2   + bmuu ⊺     Q1 0 0 Q2   ⊺ , 其中 u =   Q1 0 0 Q2   ⊺ v =   Q ⊺ 1 的最后一列 Q ⊺ 2 的第一列   . 令 α = bm, D = diag(Λ1,Λ2) = diag(d1, d2, . . . , dn), 并假定 d1 ≥ d2 ≥ · · · ≥ dn. 则 T 的特征值与 D + αuu ⊺ 的特征值相同. http://math.ecnu.edu.cn/~jypan 20/77

秦 考虑D+auuT的特征值 设入是D+au「的一个特征值，若D一入I非奇异，则 det(D+auuT-入I)=det(D-入I)·det(I+a(D-λI)-1uu) 故det(I+a(D-λI)-1uuT)=0. 引理设x,y∈R”,则det(I+xy)=1+yx. 于是 det(I+a(D-X))=1+ou(D-u=1+a 台4-入 f) 故求A的特征值等价于求特征方程f(入)=0的根。 http://math.ecnu.edu.cn/-jypan 21/77

考虑 D + αuu ⊺ 的特征值 设 λ 是 D + αuu ⊺ 的一个特征值, 若 D − λI 非奇异, 则 det(D + αuu ⊺ − λI) = det(D − λI) · det(I + α(D − λI) −1uu ⊺ ). 故 det(I + α(D − λI) −1uu ⊺ ) = 0. 引理 设 x, y ∈ R n , 则 det(I + xy ⊺ ) = 1 + y ⊺ x . 于是 det(I + α(D − λI) −1uu ⊺ ) = 1 + αu ⊺ (D − λI) −1u = 1 + α Xn i=1 u 2 i di − λ ≜ f(λ) 故求 A 的特征值等价于求特征方程 f(λ) = 0 的根. http://math.ecnu.edu.cn/~jypan 21/77