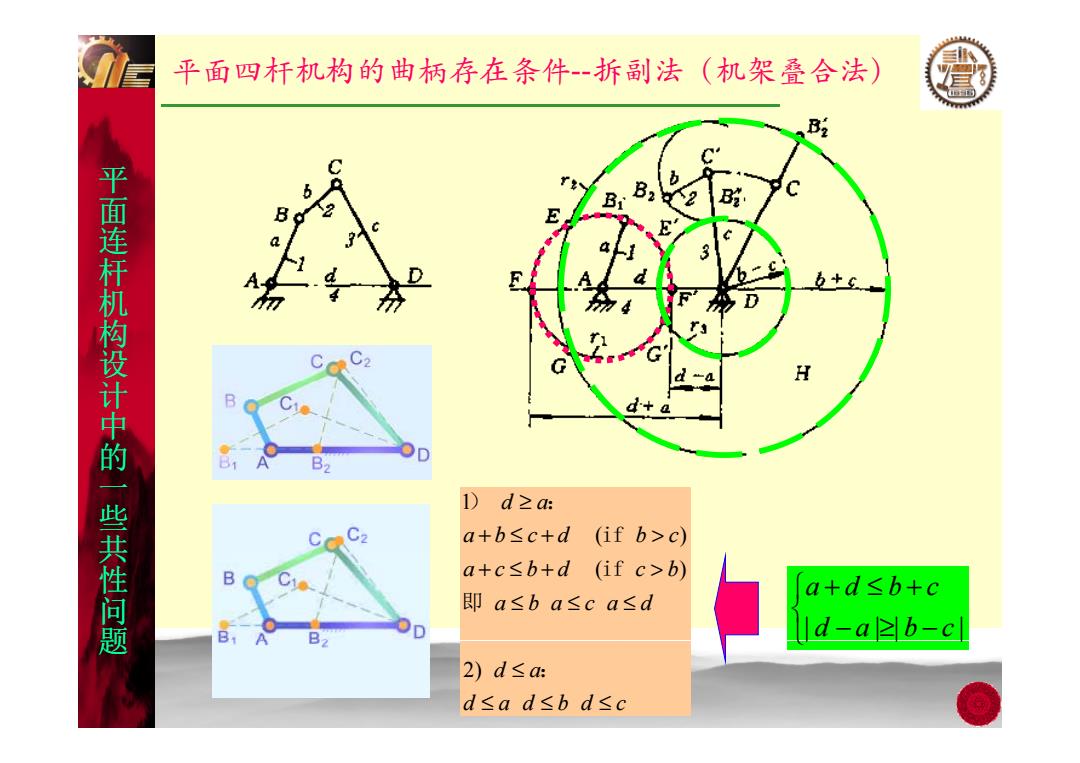
平面四杆机构的曲柄存在条件-拆副法(机架叠合法) B吃 B 平面连杆机构设计中的一些共性问题 H B B 1) d≥a: a+b≤c+d (if b>c) B a+c≤b+d (if c>b) a+d≤b+c 即a≤ba≤ca≤d d-azb-c 2)d≤ d≤ad≤bd≤c
平面四杆机构的曲柄存在条件--拆副法(机架叠合法) 平 面 连杆 机 面 构设 计中 的 一些 共 的 1 ( ) d a abcd bc ≥ +≤+ > ) : 共 if 性问 题 共 | || | ad bc da bc + ≤+ −≥− acbd cb ( ) a ba ca d +≤+ > ≤≤≤ if 即 题 | || | 2) d a d ad bd c ≤ ≤≤≤ :
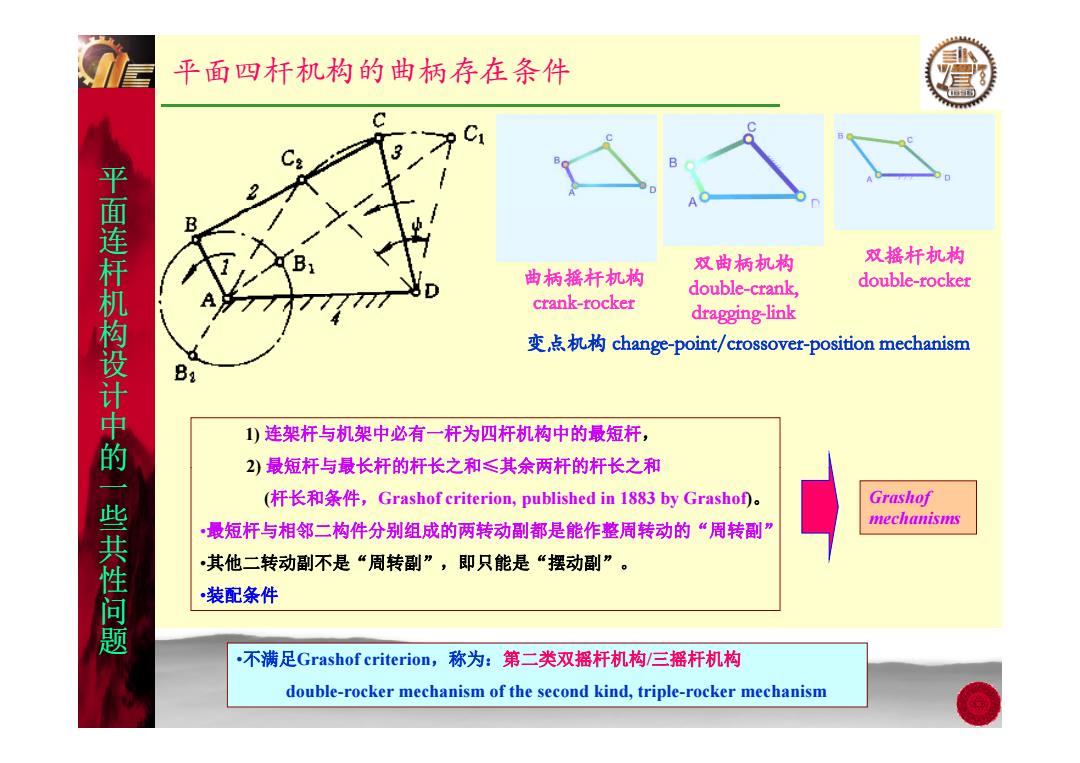
平面四杆机构的曲柄存在条件 1 B 双摇杆机构 平面连杆机构设计中的一些共性问题 双曲柄机构 曲柄摇杆机构 double-crank, double-rocker crank-tocker dragging-link 变,点机构change-point/crossover-position mechanism 1)连架杆与机架中必有一杆为四杆机构中的最短杆, 2)最短杆与最长杆的杆长之和≤其余两杆的杆长之和 (杆长和条件,Grashof criterion,published in 1883 by Grashot)。 Grashof mechanisms •最短杆与相邻二构件分别组成的两转动副都是能作整周转动的“周转副” •其他二转动副不是“周转副”,即只能是“摆动副”。 装配条件 ,不满足Grashof criterion,称为:第二类双摇杆机构/三摇杆机构 double-rocker mechanism of the second kind,triple-rocker mechanism
平面四杆机构的曲柄存在条件 平 面 连杆 机 面 曲柄摇杆机构 crank-rocker 双曲柄机构 doubl e-crank, 双摇杆机构 机 double-rocker 构设 crank-rocker doubl e-crank, dragging-link 变点机构 change-point/crossover-position m echanism 1) 连架杆与机架中必有一杆为四杆机构中的最短杆, 2) 最短杆与最长杆的杆长之和 ≤其余两杆的杆长之和 计中 的 2) 最短杆与最长杆的杆长之和 ≤其余两杆的杆长之和 (杆长和条件,Grashof criterion, published in 1883 by Grashof)。 •最短杆与相邻二构件分别组成的两转动副都是能作整周转动的“周转副” 其他 转 转 能 的 一些 共 的 Grashof mechanisms •其他 二 转动副不是“周 转副”,即只 能是“摆动副”。 •装配条件 共 性问 题 共 •不满足Grashof criterion,称为:第二类双摇杆机构/三摇杆机构 double-rocker mechanism of the second kind, triple-rocker mechanism
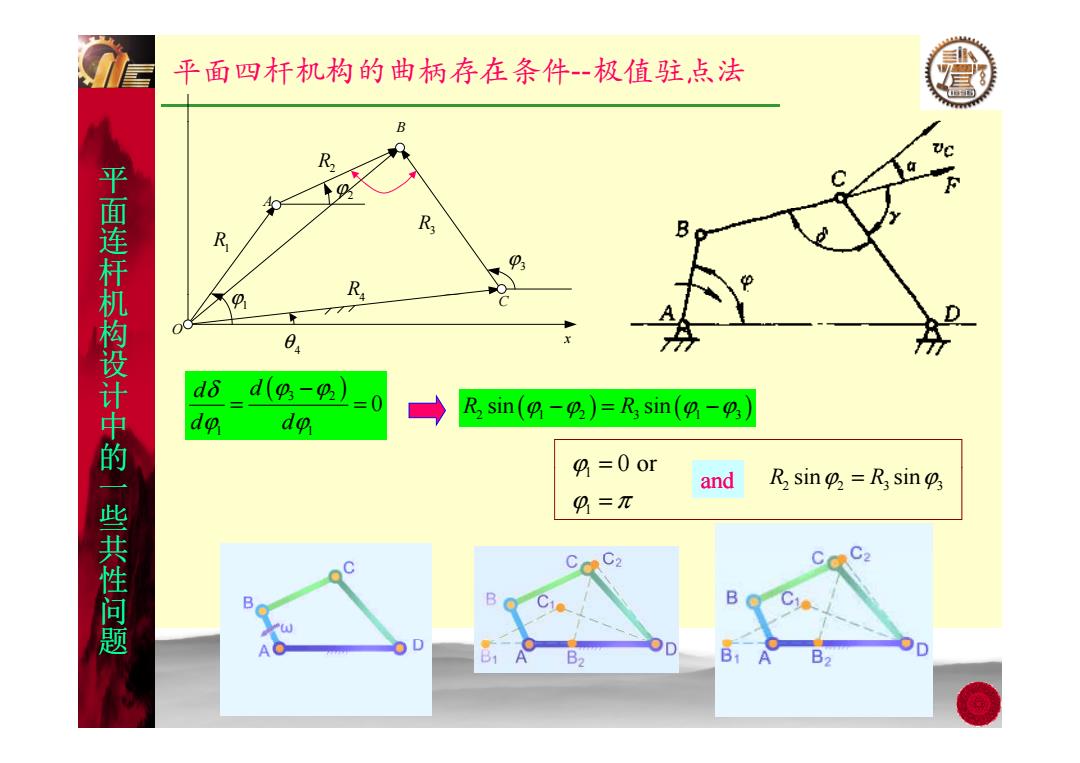
平面四杆机构的曲柄存在条件-极值驻,点法 B R R B R 平面连杆机构设计中的一些共性问题 R 777 84 do d9-0) =0 do do R sin(o-)=Rs sin(- 9=0or and R sin=R3 sin 9=π C B B
jy平面四杆机构的曲柄存在条件--极值驻点法 平 面 R2 ϕ2 A B 面 连杆 机 面 R1 ϕ R3 ϕ3 机 R4 构设 d δ d ( ) x O ϕ1 R4 θ 4 C 计中 的 ( 3 2 ) 1 1 0 d d d d δ ϕ ϕ ϕ ϕ − = = R R 2 12 3 13 sin sin () () ϕϕ ϕϕ −= − 1 ϕ = 0 or 的 一些 共 的 1 1 ϕ 0 or ϕ = π 2 23 3 an d R R sin sin ϕ ϕ = 共 性问 题 共
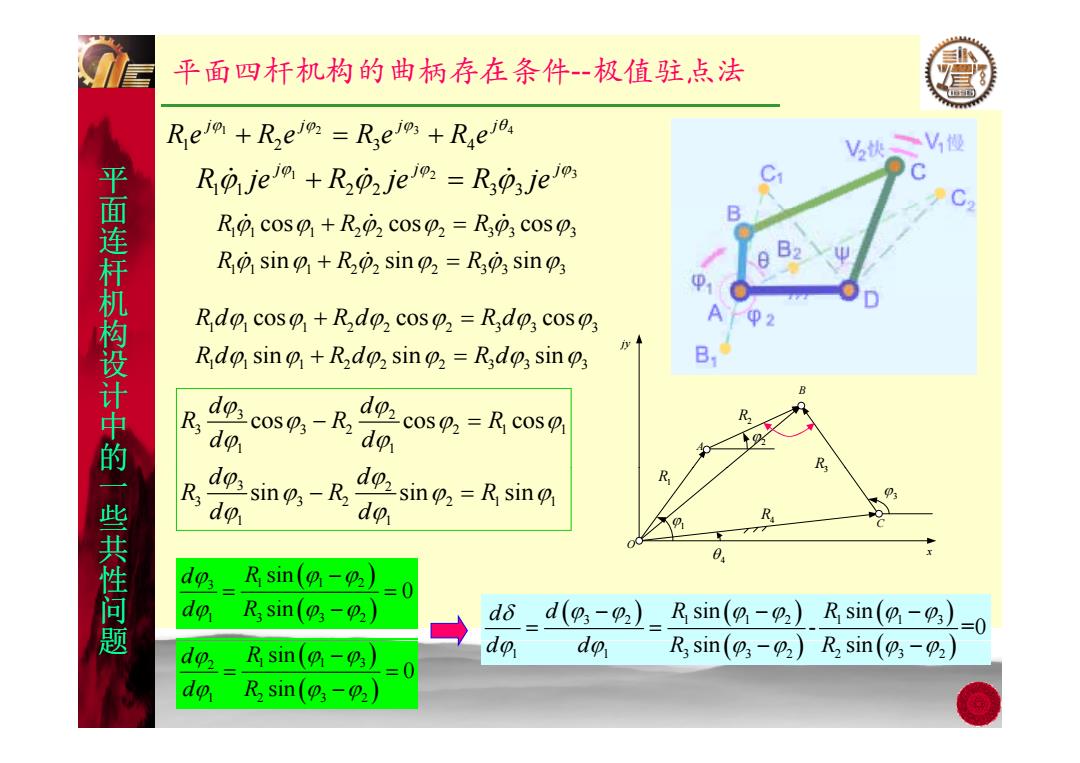
平面四杆机构的曲柄存在条件-极值驻,点法 Re+Re1p:=Rel+Reio 吃快V慢 Rije+Rapzje=R3osje oc C2 Rio coso+Roz cos2=R3o coso; 平面连杆机构设计中的一些共性问题 Rio sin o+R02 sin2 R0 sin s R do coso+Rdo,cosp=Rdo;cosps φ2 Rdo sino+Rdo sinp2=Rdo;sin B R do do cos dozco=Rcos R R do sin-Rdo sin=Rsin do R sin(-2) 0 do R,sin(-2) d8 d(g-0,)_Rsin(g-0).Rsin(9-0,)=0 do Rsin(01-03 do do R sin(o-2)Rsin(o-2) do R,sin(o-2)
j j j j 平面四杆机构的曲柄存在条件--极值驻点法 平 面 1 2 3 4 1 2 3 4 j j j j R e R e R e R e 1 2 3 1 1 2 2 3 3 j j j 面 R je R je R je 连杆 机 面 11 1 2 2 2 3 3 3 11 1 2 2 2 3 3 3 cos cos cos sin sin sin RR R RR R 机 构设 jy 11 1 2 2 2 33 3 11 1 2 2 2 3 3 3 cos cos cos sin sin sin Rd Rd Rd Rd Rd Rd 计中 的 R2 2 R3 A B 3 2 3 32 2 1 1 1 1 cos cos cos d d RR R d d d d 的 一些 共 的 x O R1 1 R3 3 R4 C 3 2 3 32 2 1 1 1 1 sin sin sin d d RR R d d 共 性问 题 共 x 4 3 1 12 1 3 32 sin 0 sin d R d R 32 1 12 1 13 sin sin - =0 i i d dR R ddR R 题 2 1 13 1 2 32 sin 0 sin d R d R ddR R 1 1 3 32 2 32 sin s in
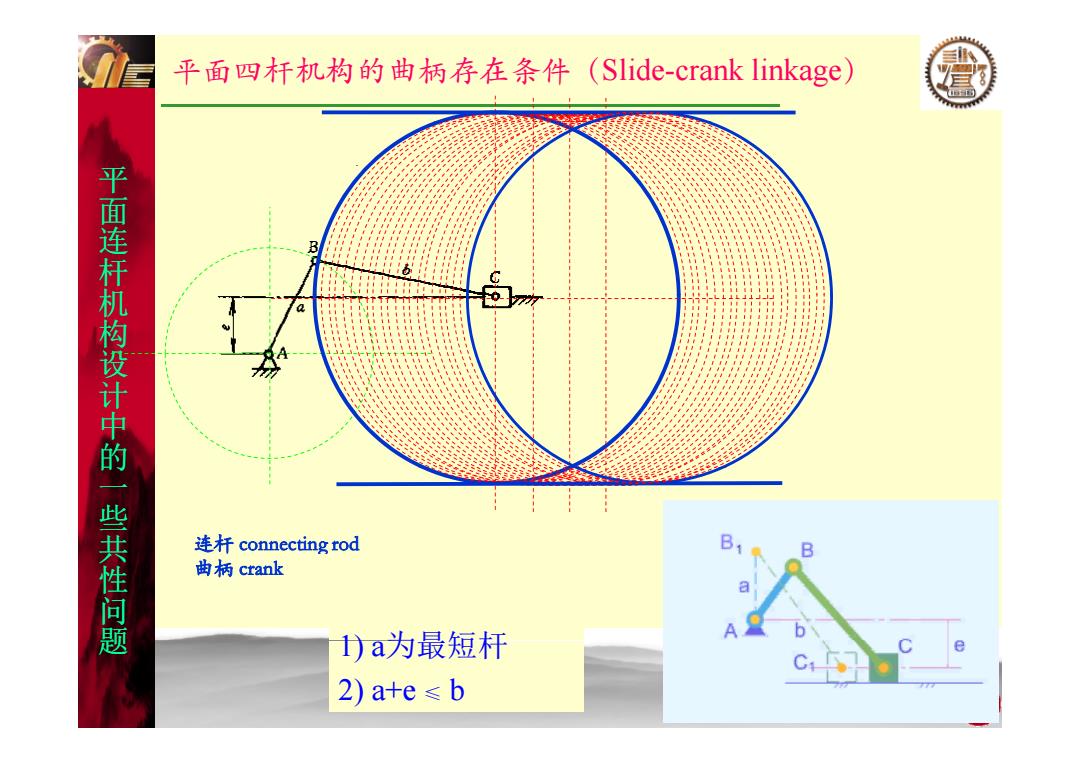
平面四杆机构的曲柄存在条件(Slide-crank linkage) B 平面连杆机构设计中的一些共性问题 连杆connecting rod 曲柄crank 1)a为最短杆 2)a+e≤b
平面四杆机构的曲柄存在条件(Slide-crank linkage ) 平 面 连杆 机 面 构设 计中 的 一些 共 的 性问 连杆 connecting rod 题 共 1) 为最短杆 曲柄 crank 题 a 2) a+e ≤ b