As(t) Ah(t) (a) (b) 0 2 (c) 图8-3信号时间波形
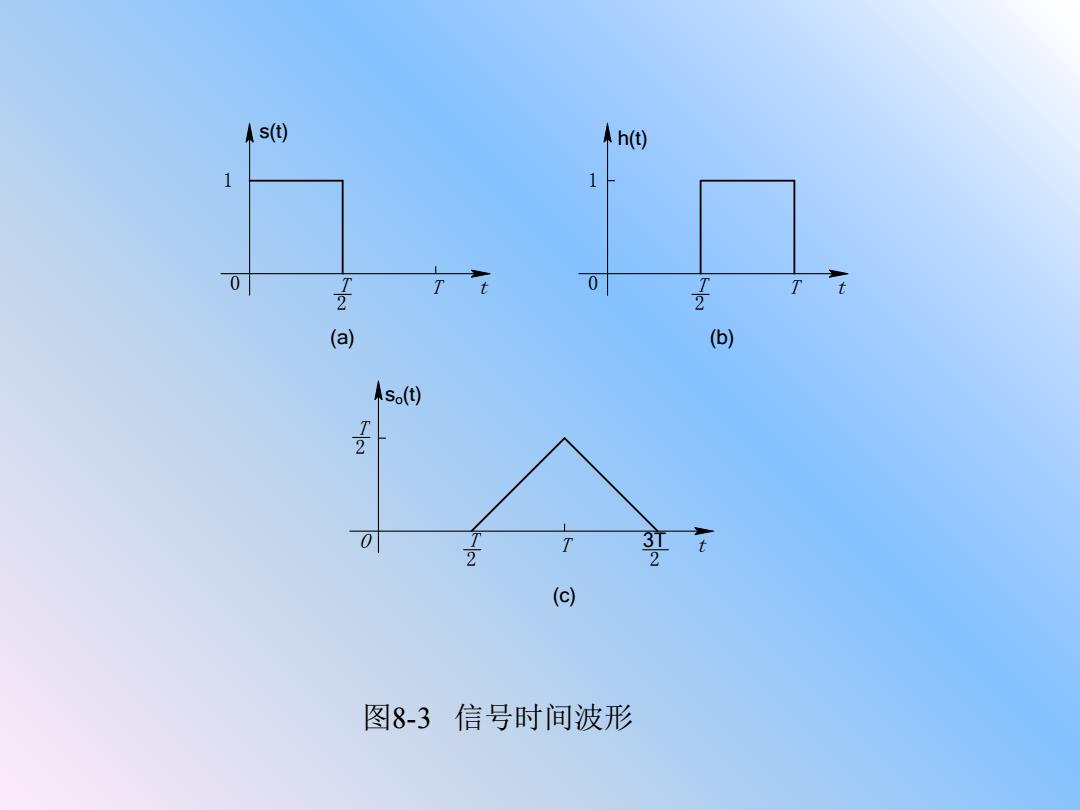
图8-3 信号时间波形 (a) (b) so(t) O T t (c) 2 T 2 T 2 T 2 3T s(t) 0 T t 2 T 1 h(t) 0 T t 1

Ss()ediedt 匹配滤波器的传输函数为 H(o)-S*()e-=( -1)e-joto jo 匹配滤波器的单位冲激响应为 h(t)-s(to-t) 取。=T,则有 o=e令-Ue jo h(t)=s(T-)
2 0 S( )= ( ) ω ω ω ∞ − − −∞ = ∫ ∫ T j t j t s t e dt e dt 2 1 (1 ) ω ω − = − T j e j 匹配滤波器的传输函数为 0 0 2 1 H( )=S*( ) ( 1) ω ω ω ω ω ω − − = − T j j t j t e ee j 匹配滤波器的单位冲激响应为 h(t)=s(t0-t) 取t0=T,则有 2 1 ( ) ( 1) T j j T H ee j ω ω ω ω − − = − h(t)=s(T-t)

匹配滤波器的单位冲激响应如图8-3(b)所示。 (2)由式(8.1-20)可得匹配滤波器的输出为 s.(t)=R(t-to)=[s(x)s(x+t-to)dx T +t, 3T 2 t, T<12 0, 其他 匹配滤波器的输出波形如图8-3(c)所示。可见, 匹配滤 波器的输出在仁T时刻得到最大的能量 E
匹配滤波器的单位冲激响应如图 8 - 3(b)所示。 (2) 由式(8.1 - 20)可得匹配滤波器的输出为 o 0 0 s (t)=R(t-t )= ( ) ( ) s x s x t t dx ∞ −∞ + − ∫ , 2 t T − + 3 , 2 T − t 0, t T T ≤ ≤ 2 2 3T T ≤ t ≤ 其他 = 匹配滤波器的输出波形如图 8 - 3(c)所示。可见,匹配滤 E= 2 波器的输出在 T t=T时刻得到最大的能量

8.2最小差错概率接收准则 8.2.1数字信号接收的统计模型 在数字信号的最佳接收分析中,我们不是采用先给出接 收机模型然后分析其性能的分析方法,而是从数字信号接收 统计模型出发,依据某种最佳接收准则,推导出相应的最佳 接收机结构,然后再分析其性能。 数字通信系统的统计模型如图8·4所示。图中消息空间、 信号空间、噪声空间、观察空间及判决空间分别代表消息、 发送信号、噪声、接收信号波形及判决结果的所有可能状态 的集合。各个空间的状态用它们的统计特性来描述
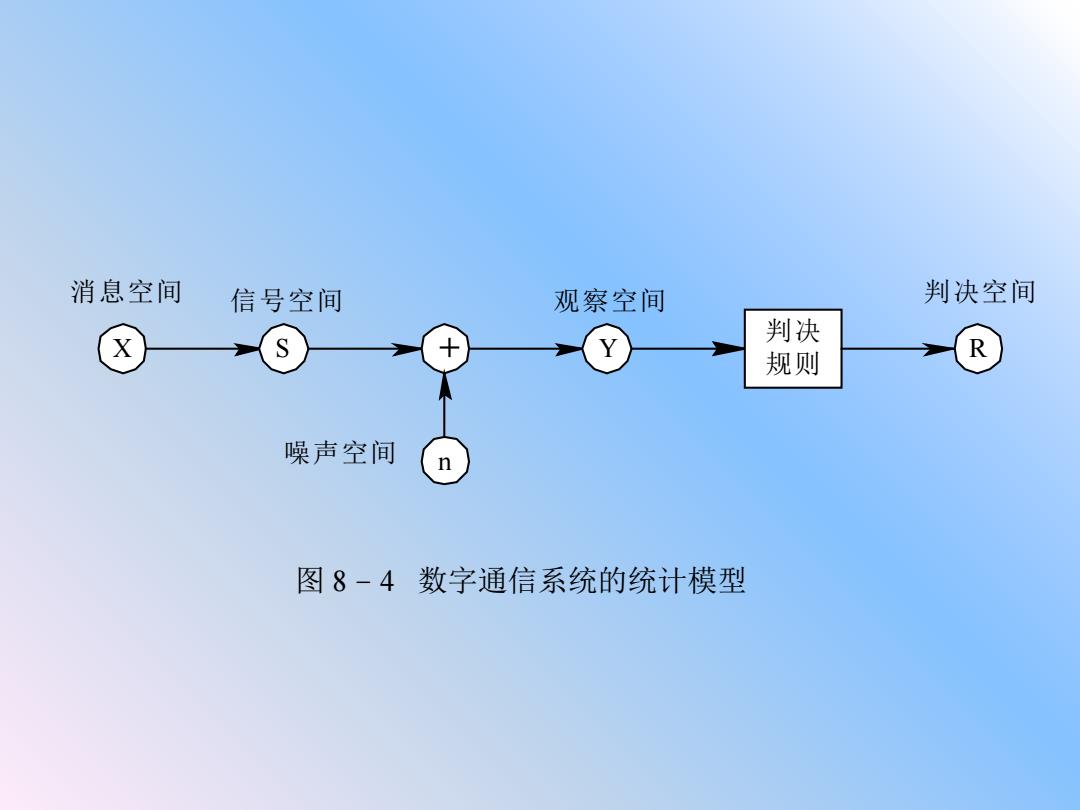
8.2 最小差错概率接收准则 8.2.1数字信号接收的统计模型 在数字信号的最佳接收分析中,我们不是采用先给出接 收机模型然后分析其性能的分析方法,而是从数字信号接收 统计模型出发,依据某种最佳接收准则,推导出相应的最佳 接收机结构,然后再分析其性能。 数字通信系统的统计模型如图 8 - 4 所示。 图中消息空间、 信号空间、噪声空间、观察空间及判决空间分别代表消息、 发送信号、噪声、接收信号波形及判决结果的所有可能状态 的集合。各个空间的状态用它们的统计特性来描述
消息空间 信号空间 观察空间 判决空间 Y 判决 规则 噪声空间 图8-4数字通信系统的统计模型
图 8 – 4 数字通信系统的统计模型 X S + Y 判决 规则 R n 消息空间 信号空间 观察空间 判决空间 噪声空间