
国家重点实验室 第2章随机过程 2.1随机过程的基本概念和统计特性 2.2平稳随机过程 2.3高斯随机过程 2.4随机过程通过线性系统 2.5窄带随机过程 2.6正弦波加窄带高斯噪声 返回主且录
2.1随机过程的基本概念和统计特性 2.2平稳随机过程 2.3高斯随机过程 2.4随机过程通过线性系统 2.5窄带随机过程 2.6正弦波加窄带高斯噪声 第 2 章随机过程 返回主目录

国家重点实验室 本章要求: ◆随机过程的基本概念和数字特征(均值、方差、相关 函数); ◆平稳、高斯、窄带、正弦波加窄带高斯过程的统计特 性 ◆随机过程通过线性系统 ◆高斯白噪声和带限白噪声 西安皂子积科接大学
本章要求: 随机过程的基本概念和数字特征(均值、方差、相关 函数); 平稳、高斯、窄带、正弦波加窄带高斯过程的统计特 性 随机过程通过线性系统 高斯白噪声和带限白噪声 西安电子科技大学

国家重点实验室 2.1随机过程的基本概念和统计特性 2.1.1随机过程 自然界中事物的变化过程可以大致分成为两类。一类是其 变化过程具有确定的形式,或者说具有必然的变化规律,用 数学语言来说,其变化过程可以用一个或几个时间的确定函 数来描述,这类过程称为确定性过程。例如,电容器通过电 阻放电时,电容两端的电位差随时间的变化就是一个确定性 函数。而另一类过程没有确定的变化形式,也就是说,每次 对它的测量结果没有一个确定的变化规律,用数学语言来说, 这类事物变化的过程不可能用一个或几个时间的确定函数来 描述,这类过程称为随机过程。下面我们给出一个例子:
2.1 随机过程的基本概念和统计特性 2.1.1随机过程 自然界中事物的变化过程可以大致分成为两类。一类是其 变化过程具有确定的形式,或者说具有必然的变化规律,用 数学语言来说,其变化过程可以用一个或几个时间t的确定函 数来描述,这类过程称为确定性过程。例如,电容器通过电 阻放电时,电容两端的电位差随时间的变化就是一个确定性 函数。而另一类过程没有确定的变化形式,也就是说,每次 对它的测量结果没有一个确定的变化规律,用数学语言来说, 这类事物变化的过程不可能用一个或几个时间t的确定函数来 描述,这类过程称为随机过程。下面我们给出一个例子:

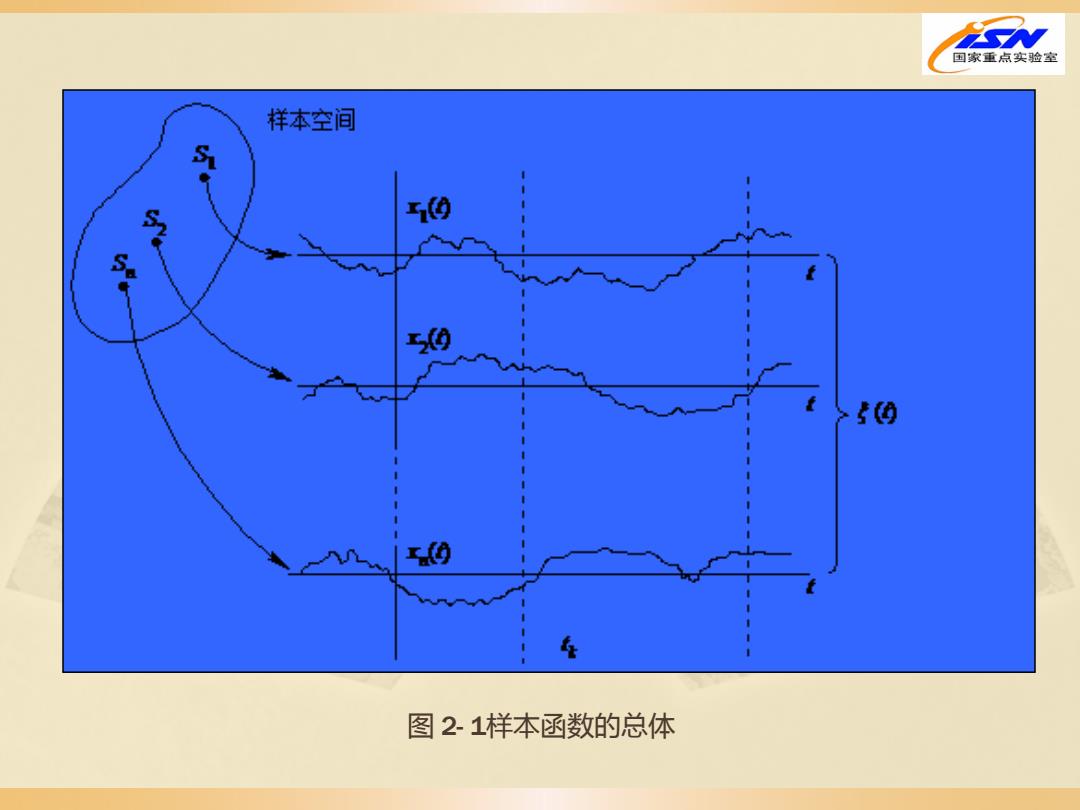
设有n台性能完全相同的接收机。我们在相同的工作环境 和测试条件下记录各台接收机的输出噪声波形(这也可以理解 为对一台接收机在一段时间内持续地进行n次观测)。测试结 果将表明,尽管设备和测试条件相同,记录的条曲线中找不 到两个完全相同的波形。这就是说,接收机输出的噪声电压随 时间的变化是不可预知的,因而它是一个随机过程。 由此我们给随机过程下一个更为严格的定义:设S(k=1, 2,)是随机试验。每一次试验都有一条时间波形(称为样本 函数或实现),记作x①,所有可能出现的结果的总体{x(①), x2(),…,X(),…}就构成一随机过程,记作ξ)。简言之,无 穷多个样本函数的总体叫做随机过程,如图2-1所示
设有n台性能完全相同的接收机。我们在相同的工作环境 和测试条件下记录各台接收机的输出噪声波形(这也可以理解 为对一台接收机在一段时间内持续地进行n次观测)。测试结 果将表明,尽管设备和测试条件相同,记录的n条曲线中找不 到两个完全相同的波形。这就是说,接收机输出的噪声电压随 时间的变化是不可预知的,因而它是一个随机过程。 由此我们给随机过程下一个更为严格的定义:设Sk(k=1, 2, …)是随机试验。 每一次试验都有一条时间波形(称为样本 函数或实现),记作xi (t),所有可能出现的结果的总体{x1(t), x2(t), …, xn(t), …}就构成一随机过程,记作ξ(t)。简言之, 无 穷多个样本函数的总体叫做随机过程,如图 2 - 1 所示
S 国家重点实验室 样本空间 G 图21样本函数的总体
图 2- 1样本函数的总体