
第一章勾股定理 核心·重难探究 知识点勾股定理的应用 【方法归纳】 【例1】如图, 只蚂蚁从实心长方体 B 解与长方体有关的最短线路问题,只需对 的顶点A出发,沿长 长方体进行部分展开,画出局部的展开图,利用 方体的表面爬到对角 两点之间线段最短与勾股定理求解.若将长方体 顶点C处,请你帮蚂蚁设计一条最短的爬行 全部展开,不仅没有必要反而会扰乱视线, 线路,蚂蚁要爬行的最短路程为多少? 【例2】小明与小亮 跟家人到海岛去玩寻宝 1北 思路分析(1)你能将长方体展开成平面 游戏.如图,他们到达后, 图形吗?有几种情况?(2)点A到点C的最 先向正东走了8km,再向 短线路是什么?在展开图中画出来.(3)发现 展开图中的直角三角形了吗?应用勾股定理 正北走,走了2km,遇上 能求出蚂蚁爬行的最短路程为多少吗? 礁石,只好改道向正西 走,走了3km后,再向正A 解蚂蚁由点A沿长方体的表面爬行到 北走6km,再向正东走1km,找到了藏宝的 点C1,有三种方式,分别展成平面图形如下: 地点.求藏宝的地点离到达点的距离. C 思路分析实际问题→构造直角三角形→ 应用勾股定理→解决实际问题, 解如图,过点B作BDL B AC于点D,连接AB. 图① 图② 在Rt△ABD中,AD= 0 8-3+1=6(km),BD=2+ 72 6=8(km).由勾股定理,得 1 A 4 AB2=AD2+BD2=62+ D 图③ 82=10,所以AB=10km. 如图①,在Rt△ABC1中,AC=AB+ 故藏宝的地点离到达点的距离是10km. BC=42+32=25. 【方法归纳】 如图②,在Rt△ACC1中,AC号=AC2+ CC=62+12=37. 本题的解决体现了数学建模思想,即把 如图③,在Rt△ABC1中,AC=AB+ 实际问题转化为数学问题.由于正东方向与 B1C=5+22=29. 正北方向的夹角是直角,正西方向与正北方 因为25<29<37,所以沿图①的方式爬 向的夹角也是直角,于是想到构造直角三角 行路线最短,最短路程是5. 形,利用勾股定理来解这道题目. 新知·训练巩固 1.两只小鼹鼠在地下同时从同一处开始打 只小鼹鼠相距(A). 洞,一只朝北面挖,每分钟挖8c,另一只 A.100 cm B.50 cm 朝东面挖,每分钟挖6cm,10分钟之后两 C.140 cm D.80 cm 9
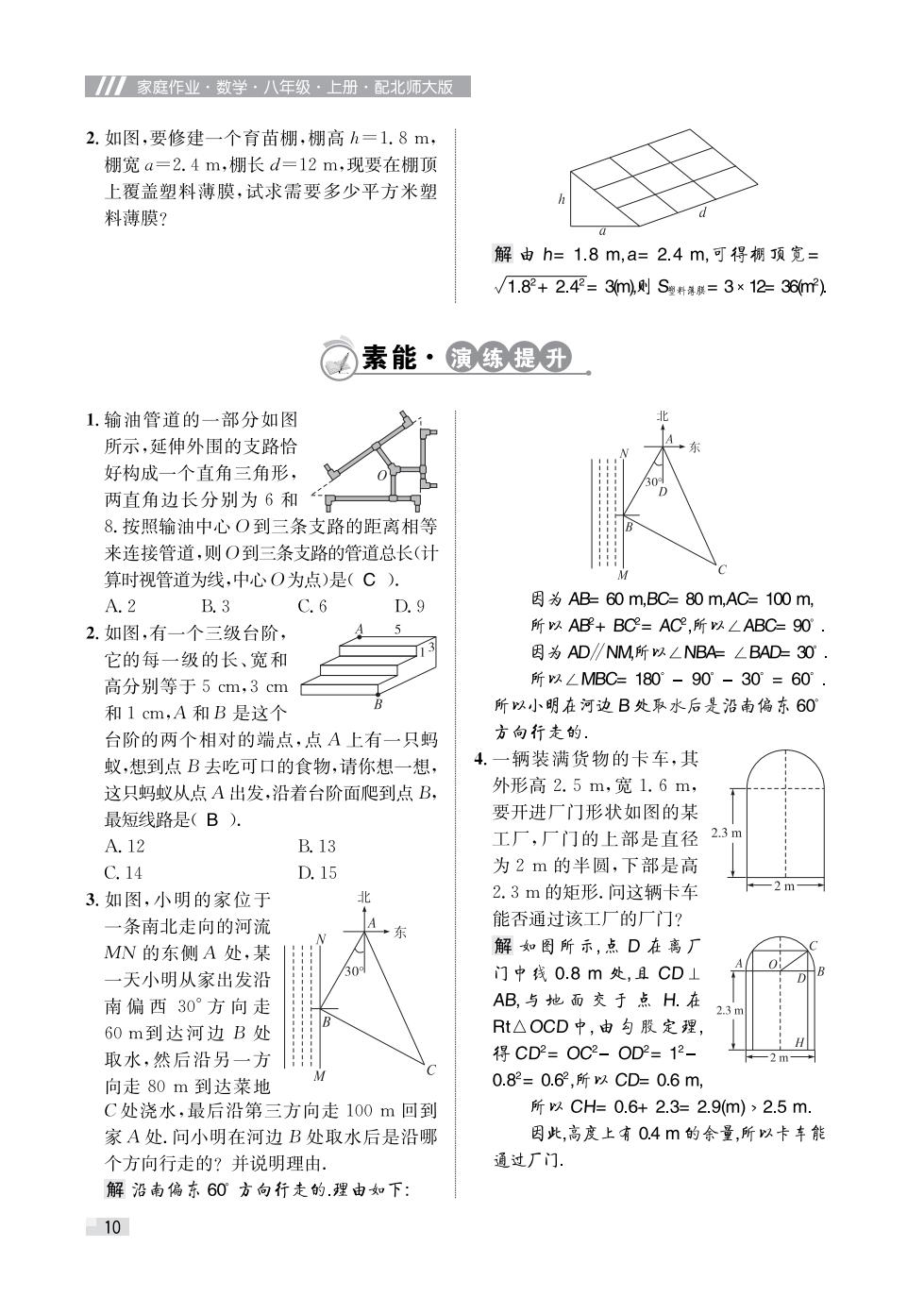
1家庭作业·数学·八年级·上册·配北师大版 2.如图,要修建一个育苗棚,棚高h=1.8m, 棚宽a=2.4m,棚长d=12m,现要在棚顶 上覆盖塑料薄膜,试求需要多少平方米塑 料薄膜? 解由h=1.8m,a=2.4m,可得棚顶宽= √/1.82+2.4=3m,则S型料,展=3×12-36m) 素能·演练提升 1.输油管道的一部分如图 所示,延伸外围的支路恰 好构成一个直角三角形, 两直角边长分别为6和 8.按照输油中心O到三条支路的距离相等 来连接管道,则O到三条支路的管道总长(计 算时视管道为线,中心O为点)是(C). A.2 B.3 C.6 D.9 因为AB60m,BC=80m,AC-100m, 2.如图,有一个三级台阶, 所以AB+BC=AC,所以∠ABC=90° 它的每一级的长、宽和 因为AD∥NM,所以∠NBA∠BAD=30 高分别等于5cm,3cm 所以∠MBC=180°-90°-30°=601 和1cm,A和B是这个 所以小明在河边B处取水后是沿南偏东60 台阶的两个相对的端点,点A上有一只蚂 方向行走的 蚁,想到点B去吃可口的食物,请你想一想, 4.一辆装满货物的卡车,其 这只蚂蚁从点A出发,沿着台阶面爬到点B, 外形高2.5m,宽1.6m, 最短线路是(B. 要开进厂门形状如图的某 2.3m A.12 B.13 工厂,厂门的上部是直径 C.14 D.15 为2m的半圆,下部是高 2.3m的矩形.问这辆卡车 -2m 3.如图,小明的家位于 北 一条南北走向的河流 A 能否通过该工厂的厂门? 东 MN的东侧A处,某 解如图所示,点D在离厂 一天小明从家出发沿 30 门中线0.8m处,且CD⊥ 南偏西30°方向走 AB,与地面交于点H.在 60m到达河边B处 Rt△OCD中,由勾股定理, 取水,然后沿另一方 得CD2=0C2-OD2=12- 2m1 向走80m到达菜地 0.82=0.6,所以CD=0.6m C处浇水,最后沿第三方向走100m回到 所以CH=0.6+2.3=2.9m)>2.5m. 家A处.问小明在河边B处取水后是沿哪 因此,高度上有0.4m的余量,所以卡车能 个方向行走的?并说明理由。 通过厂门. 解沿南偏东60方句行走的.理由如下 10

第二章 实数 1认识无理数 基础·自主梳理 1.在等式a=2中,a既不是整数,也 温馨提示 不是分数,所以a不是有理数.整数的平方 有理数与无理数的主要区别:(1)无 是整数,分数的平方是分数 理数是无限不循环小数,有理数是有限小 2.有理数都可以用有限小数和无限循 数或无限循环小数;(2)任何一个有理数 环小数表示.反过来,任何有限小数和无限 都可以化为分数的形式,而无理数不能, 循环小数都是有理数.无限不循环小数叫 做无理数. 3.如果x2=8,那么x在哪两个整数之 间:2和3. 4.写出一个在1和2之间的无理数:答案 不唯一,如1.010010001相邮两个1之间0的 个数逐次加1)等 核心·重难探究 知识点一无理数识别 理数:受,1.11211211…(南尔两个2之间1 【例1】下列各数,哪些是有理数?哪些 的个数逐次加1): 是无理数? 0,5-4,0.i2,-号1.11211211… 【误区警示】 (相邻两个2之间1的个数逐次加1),3.1415927. 1.注意3.1415927与π的区别.3.1415927 思路分析(1)哪个数是整数?哪个数是 属于有限小数,不是π,前者是有理数,后者是 分数?哪个数是无限循环小数?这些数都是 无理数 有理数吗?(2)哪个数是无限不循环小数?哪 2.不是分数,分数的分子与分母都是正 个数是含有π的数?这些数都是无理数吗? 整数 解才理数0-40,12,-3141527;无 11

1家庭作业·数学·八年级·上册·配北师大版 知识点二无理数近似值的估算 根据上述计算,可以得到: 【例2】设面积为7的正方形的边长为x, (1)x的整数部分为2; 请你回答下列问题, 2)x不是有理数.因为没有一个整数的平 (1)x的整数部分是多少? 方等于7,也没有一个分数的平方等于7.由上 (2)x是有理数吗?请简要说明理由. 面的计算知,X是无限不循环小数. 解根据题意,得=7. 【方法归纳】 当2sX<3时,4<9; 当2.6<×<2.7时,6.76<<7.29; 要估算无理数的近似值,第一步应确定被 当2.64<×<2.65时,6.9696<<7.0225; 估算无理数的整数取值范围;第二步以较小整数 当2.645<×<2.646时,6.996025X< 逐步开始加0.1(或以较大整数逐步开始减0.1), 7.001316; 并求其平方,确定被估算数的十分位…如此继 续下去,可以求出无理数的近似值, 新知·训练巩固 1.下列各数:5,1.090090009…(两个9之间 别为8cm,4cm的长方形的面积相等,则a 的取值在(D). 0的个数逐次加1),号,0,3.1415926, A.2与3之间 B.3与4之间 2.156156156…,其中是无理数的有(B). C.4与5之间 D.5与6之间 4.已知Rt△ABC的直角边AC,BC的长分别 A.1个 B.2个 C.3个D.4个 2.下列各数中,是无理数的是(B). 是2cm,3cm.则它的斜边AB的长满足什么 条件?你能用一个整数或分数表示出来吗? A.0.1 解根据匀股定理,得AB=AC+BC=22+ B.0.1234…(后面的数比前面大1) C.-2 3=13.因为13既不是一个整数的平方,也 D方 不是一个分数的平方,所以AB的长不能用 一个整数或分数表示出来 3.若边长为acm的正方形的面积与长、宽分 素能·演练提升 1.下列关于0的说法正确的是(C). A.小数 B.分数 A.0是正数 B.0是负数 C.无理数 D.不能确定 C.0是有理数 D.0是无理数 3.如图是由五个小直角三角 2.面积为6的长方形,长是宽的2倍,则宽 形组成的图形,请分别计 为(C). 算出每个小直角三角形的 12

第二章实数\ 斜边的平方的值,并填在下面的横线上 同学能拿到球吗? x2=5,y2=6,x2=7,a2=8, 解设梯子项端到地面的距离为X, 9 由题意,得X=7-2=45. 判断x,y,,a,b各数中,有理数为b,无 因为45既不是整数的平方,也不是分 理数为Xy,Z,a 数的平方, 4.八年级(2)班两名同学在打羽毛球,一不小 所以X是无理数。 心球落在一棵树上,且球距离地面6m.其 所以梯子项端到地面的距离是无理数, 中一名同学赶快搬来一架长7m的梯子, 因为6=36,45>36,所以这名同学能 架在树干上,梯子底端离树干2远,另一 拿到球. 名同学爬上梯子去拿羽毛球.问:梯子顶端 到地面的距离是有理数还是无理数?这名 2 平方根 第1课时 算术平方根 ☑基础·自主梳理 1.一般地,如果一个正数x的平方等于 知识拓展 a,即x2=a,那么这个正数x就叫做a的算术 1.只有正数和0(即非负数)才有算术 平方根,记作√a,读作“根号a”.特别地, 平方根,且算术平方根也是非负数.也就是 规定0的算术平方根是0,即√0=0 说,算术平方根√a具有双重非负性:(1)被 2.正数的算术平方根是一个正数,0的算 开方数a是一个非负数,即a≥0:(2)算术 术平方根是0,负数没有算术平方根 平方根√a本身是非负数,即√a≥0,也就 3.计算:(-1)2+9=4 是说一个正数的算术平方根是正数,0的 4.式子“√2022”表示的意义是2022的 算术平方根是0. 算术平方根· 2.负数没有算术平方根,这是因为任 何一个数的平方都不可能是一个负数 13