
儿家庭作业·数学·八年级·上册·配北师大版 温馨提示 理的正确性.在一些几何问题中,对图形 利用拼图来验证勾股定理,就是根据 进行割补拼接后,只要没有重叠,没有空 同一个图形(或两个全等的图形)面积的 隙,面积就不会改变 不同表示方法列出等式,从而验证勾股定 核心·重难探究 知识点一勾股定理的验证 知识点二 勾股定理的简单应用 【例1】用如图1所示的四个相同的直角 【例2】有一架飞机在空中水平飞行,某一 三角形(直角边为a,b,斜边为c),可以拼成如 时刻刚好飞到一个男孩头顶正上方4000m处, 图2所示的正方形.你能用图2验证勾股定 过了20s,飞机距离这个男孩头顶5000m, 理吗?说明理由. 则飞机每时飞行多少千米? 思路分析(1)根据题意画出图形,这个 图形是直角三角形吗?(2)在画出的三角形 中,已知什么?求什么?你会用勾股定理求 解吗?(3)欲求飞机每时飞行多少千米,就应 图1 图2 该知道其20s时间里飞行的路程是多少. 思路分析你能用两种方法表示图2中 解如图,在△ABC中,∠C=90°,AC= 大正方形的面积吗?这两种表示方法有什么 4000m=4km,AB=5000m=5km 关系? 由勾股定理,得BC2=AB- 解能验证勾股定理理由如下: AC=52-42=9=3,所以BC= 3 km. 大正方形的边长为C其面积可以表示为C 即飞机20s飞行3km,所以它每时飞行 大正方形的面积也可以看作是小正方形的 面积加上4个直角三角形的面积,即(b-a+ 的距离为3600x3=540km. 20 4×2ab, 【方法归纳】 所以C=b-a+4x2ab,卷理,得+ 根据题意画出正确的图形是解决问题的 b2=c2. 关键.问题的解决既体现了数学模型意识,又 体现了数形结合思想.同时要注意单位的 【方法归纳】 换算. 用不同的代数式表示同一个图形的面 积,由此建立相等关系,化简得出结论 4

第一章勾股定理 新知·训练巩固 1.张大爷离家出门散步,他先向正东走了 三角形拼成如图所示的图形.在Rt△ABC 30m,接着又向正南走了40m,此时他离 中,∠ACB=90°,若AC=b,BC=a,请你利 家的距离为(C). 用这个图形解决下列问题: A.30m B.40m C.50m D.70m (1)试说明a2+2=c2; 2.如图,在高为5m,坡面长为13m的楼梯表 (2)如果大正方形的面积是10,小正方形的 面铺地毯,地毯的长度至少需要17m. 面积是2,求(a十b)2的值. 解(1)因为大正方形面积为C,直角三角形 13m 面积为2ab,小正方形面和为(b-a,所以 3.中国古代数学家们对 d=4x ab+(a-bF=2ab+a-2ab+ 于勾股定理的发现和 b,即c2=a2+b2. 证明,在世界数学史 上具有独特的贡献和 2由题图可知,b-aY=2,4×2ab= 地位,体现了数学研 10-2=8,所以2ab=8, 究中的继承和发展.现用4个全等的直角 所aa+by=(b-a旷+4ab=2+2×8=18. 素能·演练提升 1.下列选项中,不能用来证明勾股定理的 3.如图,盒内长、宽、高分别是6cm,3cm, 是(D). 2cm,盒内可放木棒最长的长度是(B). e c D 2.如图所示,台风过后某小 A.6 cm B.7 cm C.8 cm D.9 cm 学的旗杆在B处断裂,旗 4.如图,某小区有一块直角三角形的绿地,量 杆顶部A落在离旗杆底 得两直角边AC=4m,BC=3m,考虑到这 部点C8m处,已知旗杆长16m,则旗杆断 块绿地周围还有足够多的空余部分,于是 裂的地方距底部(C). 打算将这块绿地扩充成等腰三角形,且扩 A.4m B.5 m C.6m D.8 m 充部分是以AC为一直角边的直角三角形, 5
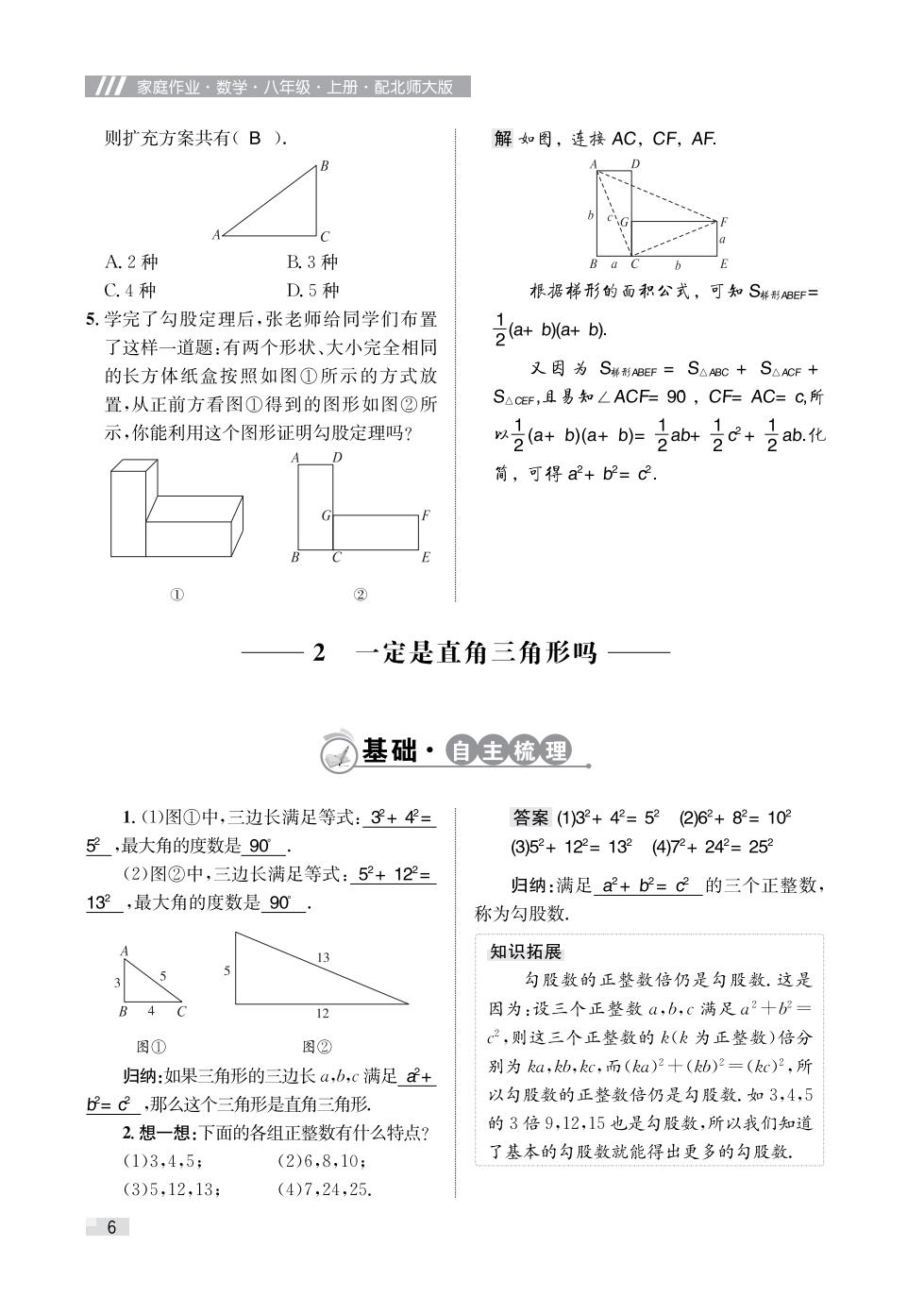
家庭作业·数学·八年级·上册·配北师大版 则扩充方案共有(B). 解如图,连接AC,CF,AF A.2种 B.3种 B a C 6 C.4种 D.5种 根据梯形的面积公式,可知S样形8EF= 5.学完了勾股定理后,张老师给同学们布置 了这样一道题:有两个形状、大小完全相同 2a+b以a+b以 的长方体纸盒按照如图①所示的方式放 又因为S梯形BEF=SAABC+S△ACF+ 置,从正前方看图①得到的图形如图②所 SACEF,且易知∠ACF=90,CF=AC=C,所 示,你能利用这个图形证明勾股定理吗? 以2a+ba+b)=2ab+2c+2ab.化 A 简,可得a+b=c2. ② 2一定是直角三角形吗 基础·自主梳理 1.(1)图①中,三边长满足等式:3+4= 答案(1)32+42=52(2)6+82=10 子,最大角的度数是90 3)52+122=132(4)72+242=252 (2)图②中,三边长满足等式:5+12= 归纳:满足a+b2=c的三个正整数, 13,最大角的度数是90 称为勾股数 3 知识拓展 勾股数的正整数倍仍是勾股数.这是 12 因为:设三个正整数a,b,c满足a2十b 图① 图② c2,则这三个正整数的k(k为正整数)倍分 归纳:如果三角形的三边长a,b,c满足子+ 别为ka,kb,kc,而(ka)2十(kb)2=(kc)2,所 仔=C,那么这个三角形是直角三角形 以勾股数的正整数倍仍是勾股数.如3,4,5 2.想一想:下面的各组正整数有什么特点? 的3倍9,12,15也是勾股数,所以我们知道 (1)3,4,5; (2)6,8,10: 了基本的勾股数就能得出更多的勾股数 (3)5,12,13; (4)7,24,25. 6

第一章勾股定理 核心·重难探究 知识点一直角三角形的判别条件 定最长边,算出最长边的平方及另两边的平 【例1】如图所 B 方和,如果最长边的平方与另两边的平方和 示,在四边形ABCD 相等,那么此三角形为直角三角形 中,AD=3cm,AB= 知识点二勾股数 4cm,∠BAD=90°, 【例2】判定下列各组数是不是勾股数: BC=12cm,CD=13cm.求四边形ABCD的 (1)7,24,25;(2)8,15,19;(3)0.6,0.8, 面积. 1.0;(4)3n,4n,5n(n>1,且n为自然数). 思路分析怎样将四边形转化为两个三 思路分析(1)各组数中的三个数都是正 角形?这两个三角形都是直角三角形吗?你 整数吗?(2)是正整数的三个数满足a2十 是怎样得到的?你能分别求出这两个三角形 b=c2吗? 的面积吗? 解(1)因为7,24,25都是正整数,且7+ 解如图所示,连 242=252,所以7,24,25是勾股数. 接BD. (2)因为82+15≠192,所以8,15,19不是 在△ABD中,AD= 勾股数. 3cmAB=4cm,∠BAD= (3)因为0.6,0.8,1.0不是正整数, 90. 所以0.6,0.8,1.0不是勾股数. 根据勾股定理,得BD=AD+AB=3+ (4)因为n>1,且n为自然数, 42=5,所以BD=5cm. 所以3n,4n,5n都是正整数. 在△BCD中,BD=5cm,BC=12cm,CD= 又(3nY+(4n2=25㎡=(5n}, 13cm,且5+12=13,所以BD+BC=CD, 所以3n,4n,5n(n>1,且n为自然数)是勾 所以△BCD是直角三角形.所以S知边形eCD= 股数 0+5 12-3 【误区警示】 【规律总结】 一组数是勾股数必须满足两个条件:(1)都 利用三角形的三边长之间的关系判断一 是正整数:(2)满足a2+=2.两者缺一不可. 个三角形是不是直角三角形的思路是:先确 新知·训练巩固 1.下列各组数是勾股数的是(D). 3.分别以下列各组数为一个三角形的三边长: A.7,12,13 B.3,4,7 ①6,8,10;②13,5,12;③2,2,3:④7,24,25 C.0.6,0.8,1 D.60,80,100 其中能构成直角三角形的有(B)组, 2.下列四组线段中,可以构成直角三角形的 A.2 B.3 C.4D.5 一组是(D). 4.在△ABC中,a=3,b=7,c2=58,则S△ABc A.1,2,3 B.32,42,5 21 c片 2 D.0.3,0.4,0.5 7

儿家庭作业·数学·八年级·上册·配北师大版 素能·演练提升 1.已知△ABC的三边分别为a,b,c,则下列 4.如图,网格中有一△ABC, 条件不能判定△ABC是直角三角形的 若小方格的边长为1,请 是(A). 你根据所学的知识, A.∠A:∠B:∠C=3:4:5 (1)求△ABC的面积: B.a:b:c=5:12:13 (2)判断△ABC是什么形状,并说明理由. C.∠C=∠A-∠B 解(1)△ABC的面和=4×4-1×2÷2-4× D.b2=a2-c2 3÷2-2×4÷2=16-1-6-4=5.故△ABC 2.若一个直角三角形的面积为6cm,斜边长 的面积为5. 为5cm,则该直角三角形的周长为12cm ②)因为小方格的边长为1,所以AB=1P+ 3.已知a,b,c是△ABC的三边长,若|a-bl+ 2=5,AC=2+4=20,BC=32+4=25, |a2+2一c2|=0,则△ABC是等腰直角 所以AB+AC=BC,所以△ABC为直 三角形 角三角形. 3勾股定理的应用 基础·自主梳理 1.解决几何体表面上两点之间的最短距 的两点之间的距离,则直接利用“两点之间线 离问题的关键是要设法把立体图形转化为平 段最短”求出线段的长度即可;若计算不同面 面图形,具体步骤是: 上的两点之间的距离,则必须把长方体(或正 (1)把立体图形展成平面图形; 方体)的表面展开,使两点转化到同一个平 (2)确定点的位置; 面内,就可以利用“两点之间线段最短”和 (3)确定直角三角形; 勾股定理加以解决了, (4)分析直角三角形的边长,用勾股定 3.用勾股定理解决实际问题的关键是从 理求解. 实际问题中构建数学模型一直角三角 2.长方体(或正方体)是立体图形,但它 形,再正确利用“两点之间线段最短”以及 的每个面都是平面,所以若计算同一个面上 勾股定理解答. 8