
家庭馆四 微专题三 利用平行四边形的判定与性质解决问题
微专题三 利用平行四边形的判定与性质解决问题
1.如图,已知点D是△ABC的边AB上一点,CE∥AB,DE交AC于 点O,且OA=OC猜想线段CD与线段AE的大小关系和位置关 系,并加以证明 E B
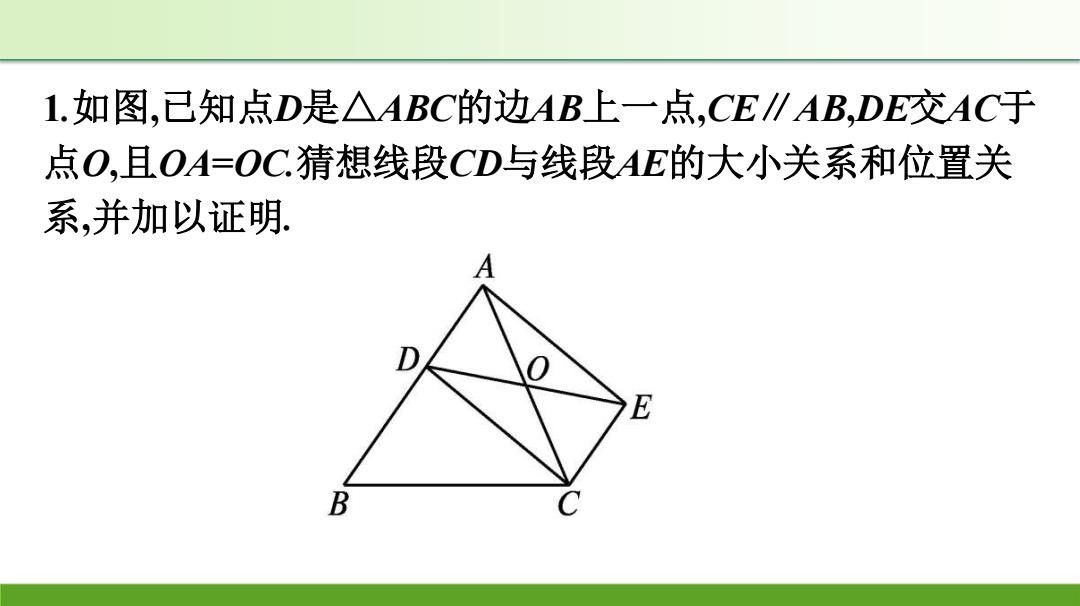
1.如图,已知点D是△ABC的边AB上一点,CE∥AB,DE交AC于 点O,且OA=OC.猜想线段CD与线段AE的大小关系和位置关 系,并加以证明

解:CD∥AE,CD=AE. 证明:CE∥AB,.·∠DAO=∠COE. 在△AOD和△COE中, .'∠DAO=∠ECO,OA=OC,∠AOD=∠EOC, .·△AOD≌△COE(ASA)..OD=OE. OA=OC, .·四边形ADCE是平行四边形. .CD∥AE,CD=AE
解:CD∥AE,CD=AE. 证明:∵CE∥AB,∴∠DAO=∠COE. 在△AOD和△COE中, ∵∠DAO=∠ECO,OA=OC,∠AOD=∠EOC, ∴△AOD≌△COE(ASA).∴OD=OE. ∵OA=OC, ∴四边形ADCE是平行四边形. ∴CD∥AE,CD=AE
2.如图,点B,E分别在AC,DF上AF分别交BD,CE于点M,N, ∠A=∠F,∠1=∠2. E 2 B (1)求证:四边形BCED是平行四边形; (2)已知DE=2,连接BN若BN平分∠DBC,求CN的长
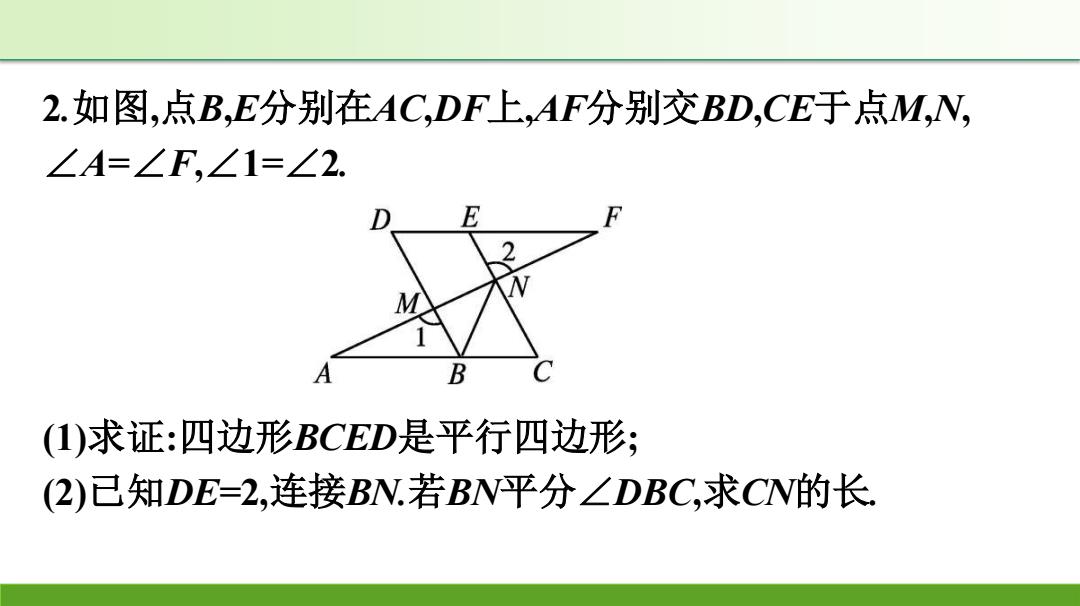
2.如图,点B,E分别在AC,DF上,AF分别交BD,CE于点M,N, ∠A=∠F,∠1=∠2. (1)求证:四边形BCED是平行四边形; (2)已知DE=2,连接BN.若BN平分∠DBC,求CN的长

(1)证明:·∠A=∠F,.DF∥AC ‘∠1=∠2,∠1=∠DMF, .·∠DMF=∠2..DB∥EC .·四边形BCED为平行四边形. (2)解:BN平分∠DBC,.·∠DBN=∠NBC. ·DB∥EC,.·∠DBN=∠BNC .·∠NBC=∠BNC..BC=CN. :四边形BCED为平行四边形, ..BC=DE=2...CN=2
(1)证明 :∵∠A=∠F,∴DF∥AC. ∵∠1=∠2,∠1=∠DMF, ∴∠DMF=∠2.∴DB∥EC. ∴四边形BCED为平行四边形. (2)解:∵BN平分∠DBC,∴∠DBN=∠NBC. ∵DB∥EC,∴∠DBN=∠BNC. ∴∠NBC=∠BNC.∴BC=CN. ∵四边形BCED为平行四边形, ∴BC=DE=2.∴CN=2