
第二节微观粒子的特性 一、微观粒子的波粒二象性 二、不确定原理
第二节 微观粒子的特性 一、微观粒子的波粒二象性 二、不确定原理

一、微观粒子的波粒二象性 1924年,法国青年物理学家德布罗意大胆预言电 子等微粒也具有波粒二象性。并指出质量为、运动 速率为)的微粒,其相应的波长入为: 餐育科学九三h起h研成果 mv 1927年,美国物理学家戴维逊和革末用电子束代 替X射线进行晶体衍射实验,得到了衍射环纹图,确 认了电子具有波动性。 1928年,实验进一步证明分子、原子、质子、中 子、粒子等微观粒子也都具有波动性。 (供药学类及医学检验专业用)
一、微观粒子的波粒二象性 1924 年,法国青年物理学家德布罗意大胆预言电 子等微粒也具有波粒二象性。并指出质量为 m、运动 速率为 的微粒,其相应的波长 为: 1927 年,美国物理学家戴维逊和革末用电子束代 替 X射线进行晶体衍射实验,得到了衍射环纹图,确 认了电子具有波动性。 1928 年,实验进一步证明分子、原子、质子、中 子、α粒子等微观粒子也都具有波动性。 h h m p = = v v
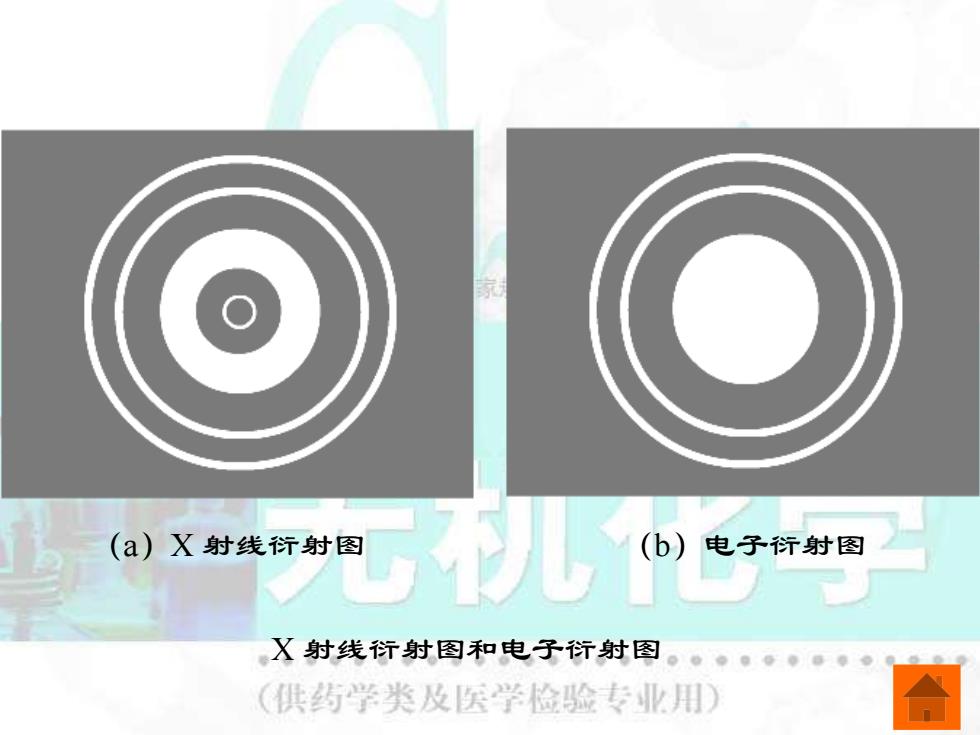
(a)X射线衍射图 (b)电子衍射图 X射线衍射图和电子衍射图。 (供药学类及医学检验专业用)
(a)X 射线衍射图 (b)电子衍射图 X 射线衍射图和电子衍射图

二、不确定原理 对于具有波粒二象性的电子,能否同时准确 地测定电子的位置和动量呢?1927年,德国物理 学家海森堡对此做出了否定回答。他认为:不可 能同时准确地测定电子的位置和动量。这就是不 确定原理,它的数学表达式为: △x△p≥h 不确定原理表明,电子位置确定得越准确, 则电子的动量就确定得越不准确;电子的动量确 定得越准确,电子的位置就确定得越不准确。 (供药学类及医学检验专业用
二、不确定原理 对于具有波粒二象性的电子,能否同时准确 地测定电子的位置和动量呢?1927年,德国物理 学家海森堡对此做出了否定回答。他认为:不可 能同时准确地测定电子的位置和动量。这就是不 确定原理,它的数学表达式为: 不确定原理表明,电子位置确定得越准确, 则电子的动量就确定得越不准确;电子的动量确 定得越准确,电子的位置就确定得越不准确。 x x p h ≥

对于原子中的电子,其运动速率约为106mS1, 质量为9.1×10-31kg, 电子的位置至少确定到原子的 大小范围(△x≈1010m)才有意义。此时电子运动速 率的不确定程度为: h 6.6×10-4J:S △U 成里7×10m:s m·△x 9.1×10-31kg×10-10m 电子运动速率的不确定程度很大,超过了电子本 身的运动速率,显然是不能忽略的。 无机化学 (供药学类及医学检验专业用)
对于原子中的电子,其运动速率约为 106 m·s −1 , 质量为 9.1×10−31 kg,电子的位置至少确定到原子的 大小范围(Δx ≈10−10 m)才有意义。此时电子运动速 率的不确定程度为: 电子运动速率的不确定程度很大,超过了电子本 身的运动速率,显然是不能忽略的。 34 6 1 31 10 6.6 10 J S 7 10 m s 9.1 10 kg 10 m x h m x − − − − = = =