
对于质量为0.01kg的子弹,运动速率为 1000ms1, 若速率的不确定程度为其运动速 率的0.1%,则其位置的不确定程度为。 h △x= m△Ux ”十五”国家规划课题研究成果 6.6×10-34Js 6.6×1034 0.01kg×(1000ms×0.1%) 宏观物体的位置不确定程度△x=108m 就已经很准确了,这样小的位置不确定程度可 以忽略不计。 (供药学类及医学俭验专业用)
对于质量为 0.01 kg 的子弹,运动速率为 1000 m·s −1,若速率的不确定程度为其运动速 率的 0.1% ,则其位置的不确定程度为。 宏观物体的位置不确定程度Δx = 10−8 m 就已经很准确了,这样小的位置不确定程度可 以忽略不计。 34 34 1 6.6 10 J s 6.6 10 0.01 kg (1000m s 0.1%) x h x m − − − = = =

第三节 氢原子结构 一、氢原子的薛定谔方程及其解 二、四个量子数 三、氢原子函数和概率密度的图形
第三节 氢原子结构 一、氢原子的薛定谔方程及其解 二、四个量子数 三、氢原子函数和概率密度的图形

氢原子的薛定谔方程及其解 1926年,奥地利著名的物理学家薛定谔提出 描述氢原子的电子的运动状态的方程,称为薛定谔 方程: ayw燕a2wo2y8π2m成e2 @2 2+02+ h2 (E+)w=0 为了求解氢原子的薛定谔方程,需要淇循畿标 变换,把直角坐标X、少、?变换成球坐标 x=r.sin0.cosp y=r.sing.sinΦ z=r·c0S0 1r=+y2+2 (供药学类及医学俭验专业用
一、氢原子的薛定谔方程及其解 1926 年,奥地利著名的物理学家薛定谔提出 描述氢原子的电子的运动状态的方程,称为薛定谔 方程: 2 2 2 2 2 2 2 2 2 8π ( ) 0 m e E x y z h r + + + + = 为了求解氢原子的薛定谔方程,需要进行坐标 变换,把直角坐标 x、y、z 变换成球坐标 r、 、 。 2 2 2 sin cos sin sin cos x r y r z r r x y z = = = = + +
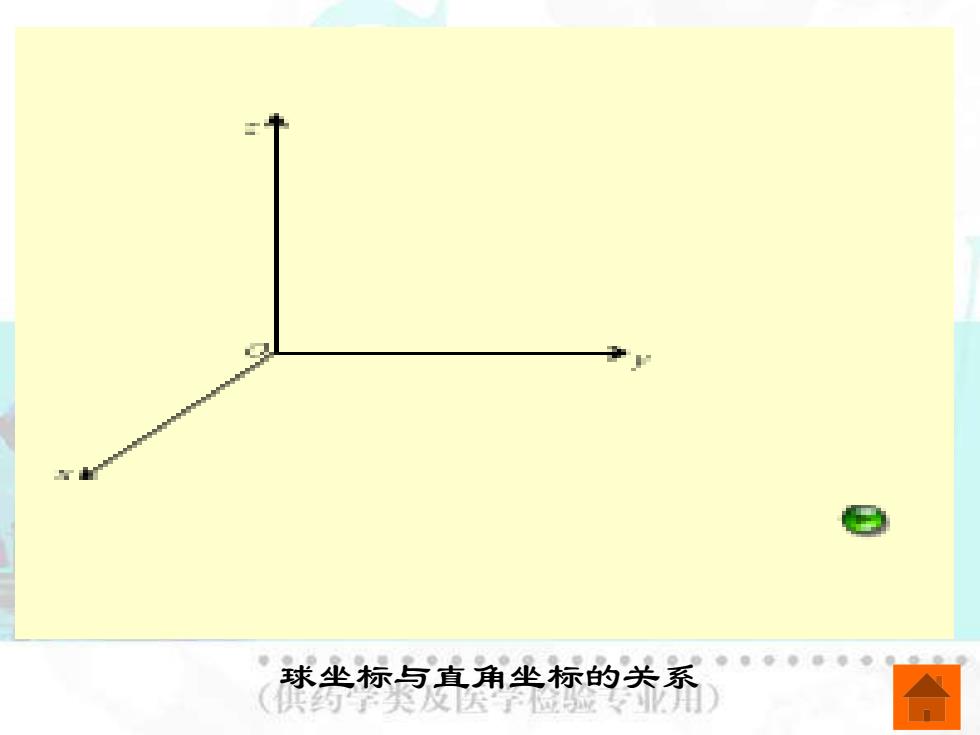
球坐标与直角坐标的关系 义天
球坐标与直角坐标的关系

氢原子在球坐标系中的薛定谔方程为: 10 a 1 -)+ r2sine 00 00 r2sin20002 a'业8pπm(E+ -)w=0 4 可以把少看作是由三个变量分别形成的函数组 成: 教育科学“十五”国家规划课题研究成果 w(r,0,p)=R(r)⊙(0)Φ(φ) 常将⊙(0)和D(中)合并为一个新函数: ”化学 Y(0,)=O(0)D(p) (供药学类及医学检验专业用)
2 2 2 2 2 2 2 2 2 2 1 1 1 8p π ( ) (sin ) ( ) 0 sin sin 4π m e r E r r r r r h r + + + + = 氢原子在球坐标系中的薛定谔方程为: 可以把 看作是由三个变量分别形成的函数组 成: 常将 和 合并为一个新函数: ( , , ) ( ) ( ) ( ) r R r = ( ) ( ) Y( , ) ( ) ( ) =