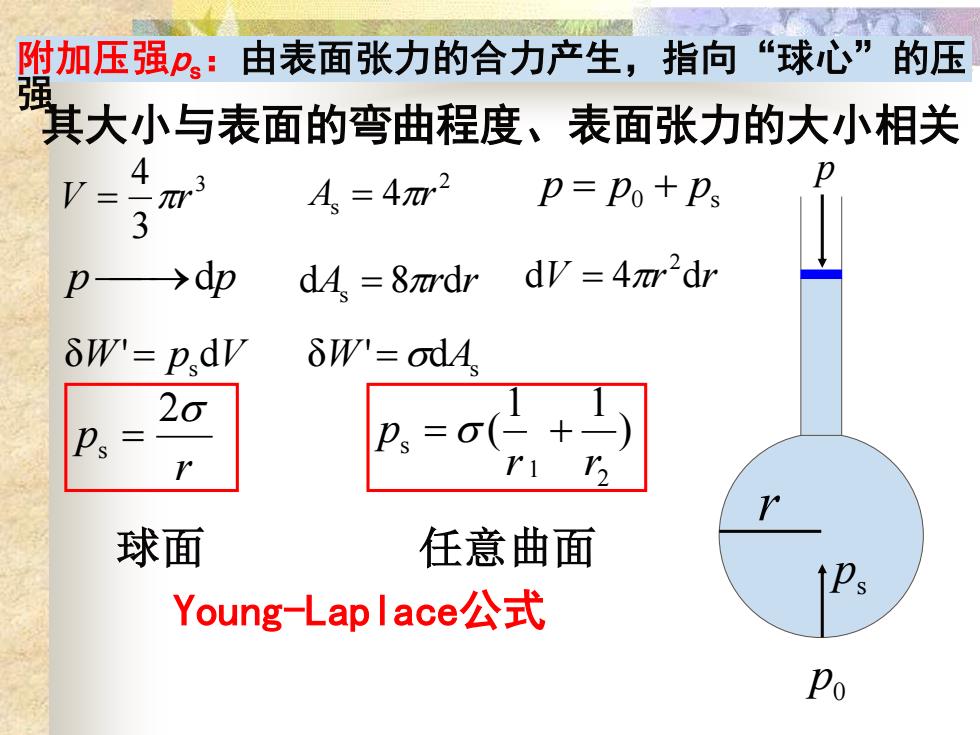
附加压强p。:由表面张力的合力产生,指向“球心”的压 其大小与表面的弯曲程度、表面张力的大小相关 V= A=42 p=Po+Ps 3 p→dp dA.=8xrd ,dV=4r2dr δW'=pdV δW'=odA 20 Ps= 1 球面 任意曲面 Young-Lap lace公式 Po
其大小与表面的弯曲程度、表面张力的大小相关 3 3 4 V = r r s p p0 2 p As = 4r p = p0 + ps p ⎯→dp dA 8 rdr s = dV 4 r dr 2 = d s δW' = ps dV δW' = A r p 2 s = ) 1 1 ( 2 1 s r r p = + Young-Laplace公式 球面 任意曲面 附加压强ps:由表面张力的合力产生,指向“球心”的压 强

适用范围: 1)适用毛细管直径<0.5mm情形 2)适用于为定值的小液滴或液体中小气泡。 注意: 1)r的符号: 凸液面,r>0,p,>0,r指向液相(固相)内部 凹液面,r<0,p<0,r指向气相 平液面,→00,、→0, 气 2)气泡的附加压强: 肥皂泡两个1-g界面,r2 Ps-Ps,1+Ps.2=40/r Ps,2
适用范围: 1)适用毛细管直径<0.5mm情形 2)适用于r为定值的小液滴或液体中小气泡。 注意: 1) r 的符号: 凸液面,r>0,ps>0, r 指向液相(固相)内部 凹液面,r <0,ps<0, r 指向气相 平液面,r→∞,ps →0, 2)气泡的附加压强: 肥皂泡两个l-g界面,r1≈r2 ps =ps,1+ ps,2 = 4σ/r r1 r2 ps,1 ps,2 气 气

例:有完全为水润湿的两似球形固体微粒,其接 触点周围有水,气/液界面的形状类似于滑轮槽, 气/液界面的曲率半径为0.02mm,滑轮槽的最小 内径为0.16mm,已知20℃时水的表面张力为 72.8×103Nm1。请定量说明水对微粒的聚结是 否有利? 解:1=-2×10-5m r2=8X105m =(+)=-2730Pa
例:有完全为水润湿的两似球形固体微粒,其接 触点周围有水,气/液界面的形状类似于滑轮槽, 气/液界面的曲率半径为0.02mm,滑轮槽的最小 内径为0.16mm,已知20℃时水的表面张力为 72.8×10-3 N·m-1。请定量说明水对微粒的聚结是 否有利? 解:r1= -2×10-5 m r2= 8×10-5 m s s l r r1 2 ) 2730Pa 1 1 ( 2 1 s = + = − r r p
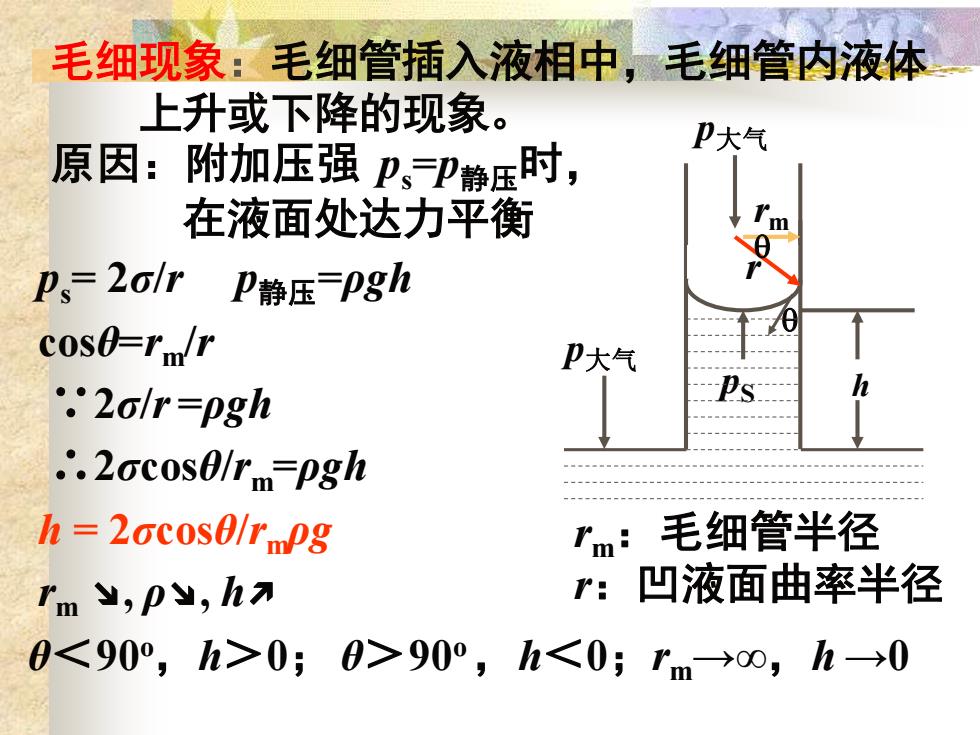
毛细现象:毛细管插入液相中,毛细管内液体 上升或下降的现象。 P大气 原因:附加压强P、静压时, 在液面处达力平衡 m p、=2alrP静压=Pgh cose=rmr P大气 ".2o/r=pgh ∴.2oc0s0lrm=pgh h 2ccos0/rmpg Im: 毛细管半径 rm ,p,ha r: 凹液面曲率半径 0<90°,h>0;0>90°,h<0;rm→o,h→0
毛细现象:毛细管插入液相中,毛细管内液体 上升或下降的现象。 原因:附加压强 ps =p静压时, 在液面处达力平衡 p大气 h p大气 pS r rm ps = 2σ/r p静压=ρgh cosθ=rm/r ∵2σ/r =ρgh ∴2σcosθ/rm =ρgh h = 2σcosθ/rmρg rm ↘, ρ↘, h↗ θ<90o ,h>0; θ>90o ,h<0;rm→∞,h →0 rm:毛细管半径 r:凹液面曲率半径
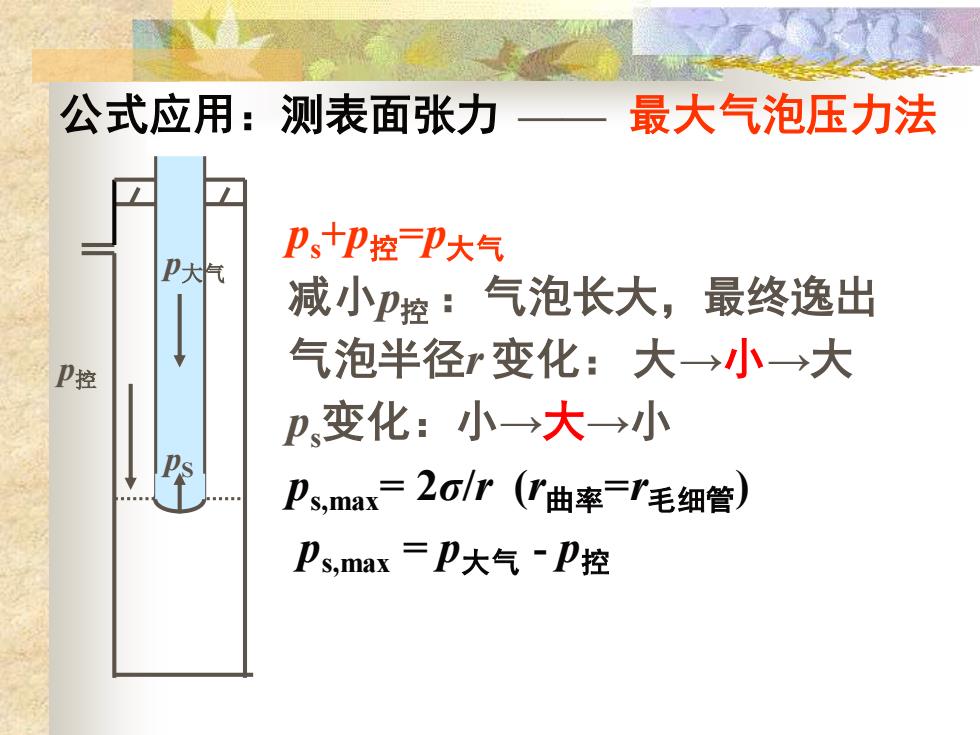
公式应用:测表面张力 最大气泡压力法 P、+P控P大气 P大 减小P控:气泡长大, 最终逸出 P控 气泡半径r变化:大→小→大 p变化:小→大→小 Psma=2or(【曲率=T毛细管) Ps,max=P大气P控
公式应用:测表面张力 —— 最大气泡压力法 ps+p控=p大气 减小p控 :气泡长大,最终逸出 气泡半径r 变化: 大→小→大 ps变化:小→大→小 ps,max = 2σ/r (r曲率=r毛细管) ps,max = p大气 - p控 p控 p大气 pS