[ M(x)M(a)ax +JM(xs)M(x)axfe=J.EIA(x(-+ px ) (-4r (-Px) (-x) d + 5PaLdx, =(0)3EIEET(4)在B处作用单位集中力偶1/4alM(s)=0 M(s)--*:截面B的转角0.-I ()()a +,(()4:E()(-)4Pa4a=0+dx, =EI3EI顺时针转向13.9.试求图示各梁截面B的挠度和转角。EI-常量al解:(1)在B处作用虚加力P和M,并列出弯矩方程raM(x)=-P,x- - M,M(x)=-{qx; -P,(I-a+x)-M,(2)上式分别对P和M求偏导数M(x) =-xiOM(x.) =-(1-a+x.)aP,aP0M(x.) = -1aM(x) =-1aM,aM,(3)用卡氏定理求挠度和转角上海理工大学力学教研室
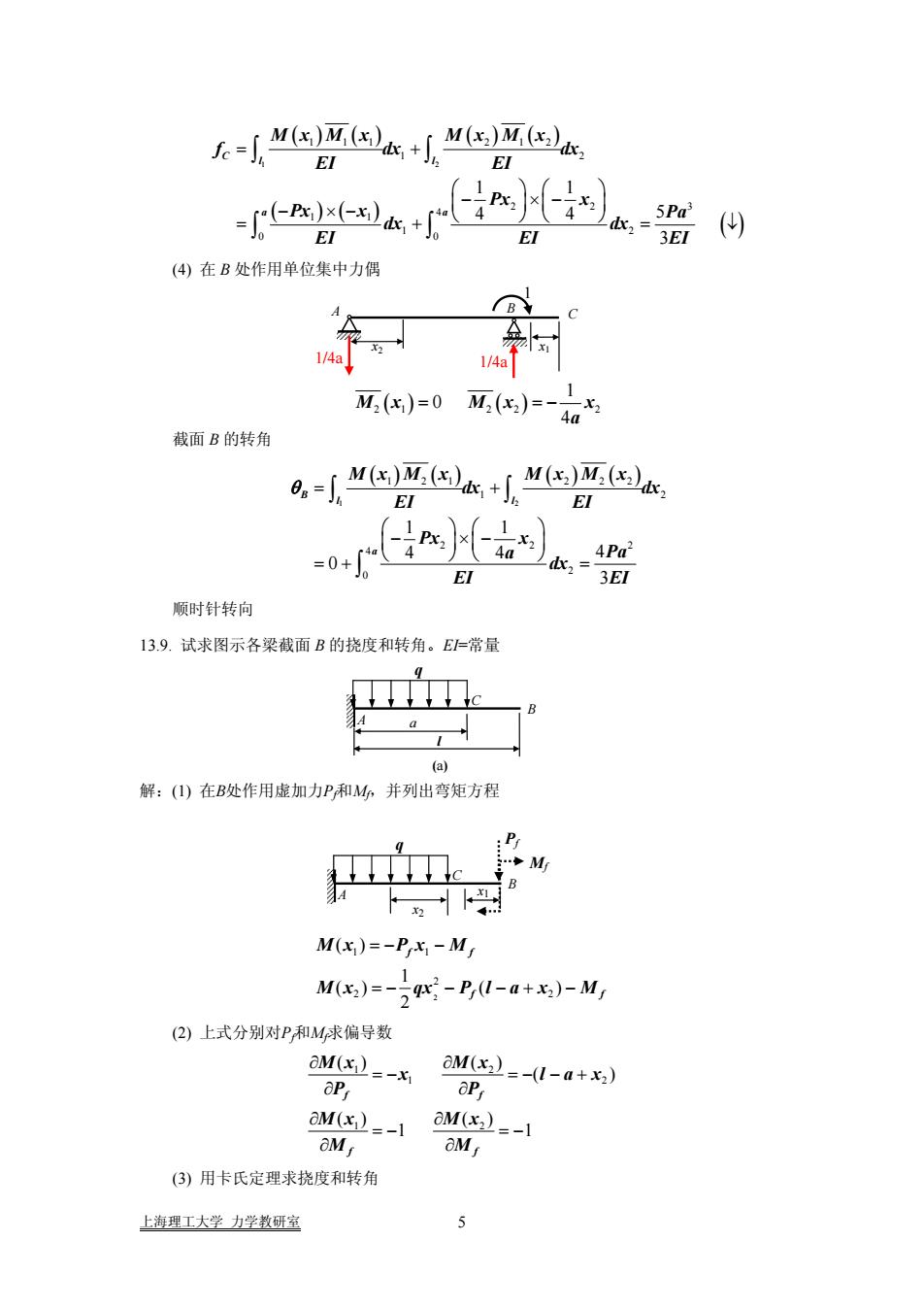
( ) ( ) ( ) ( ) ( )( ) ( ) 1 2 1 11 2 12 1 2 22 3 4 1 1 1 2 0 0 1 1 4 4 5 3 C l l a a Mx M x Mx M x f dx dx EI EI Px x Px x Pa dx dx EI EI EI = + ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ − ×− − ×− ⎝ ⎠⎝ ⎠ =+ = ∫ ∫ ∫ ∫ ↓ (4) 在 B 处作用单位集中力偶 A B C x2 x1 1 1/4a 1/4a 2 1 ( ) 2 2 ( ) 2 1 0 4 Mx Mx x a = = − 截面 B 的转角 ( ) ( ) ( ) ( ) 1 2 1 21 2 22 1 2 22 2 4 2 0 1 1 4 4 4 0 3 B l l a Mx M x Mx M x dx dx EI EI Px x a Pa dx EI EI θ = + ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ − ×− ⎝ ⎠⎝ ⎠ = + = ∫ ∫ ∫ 顺时针转向 13.9. 试求图示各梁截面 B 的挠度和转角。EI=常量 a l q B C A (a) 解:(1) 在B处作用虚加力Pf和Mf,并列出弯矩方程 x1 Mf q B C A x2 Pf 2 1 1 2 2 2 ( ) 1 () ( ) 2 f f f f Mx Px M M x qx P l a x M =− − =− − − + − (2) 上式分别对Pf和Mf求偏导数 1 2 1 2 1 2 () () ( ) () () 1 1 f f f f Mx Mx x l P P Mx Mx M M ∂ ∂ = − =− − + ∂ ∂ ∂ ∂ = − = − ∂ ∂ a x (3) 用卡氏定理求挠度和转角 上海理工大学 力学教研室 5
ou-[ M(x) aM(x)dx +J M(x,) M(x) dx,fBaP,JEIOP,EIaP,-Im2(-n)a EI2x--P(I-a+x)-M,+[-(1 - a + x2)]dx,EI- U-[ (M(d++JMETM,[ M(x,) M() te,.-0M,-I. ET oM,Igx -P,(l-a+x,)-M,- P2(-14+ --(-1)dx,EEI(4)令上两式中的P和M为零qxq_(4 -a)fs=0+()[-(1-a +x,)]dx, =-EI24EI1aqa0,=0+J°E1(-1)de=EI挠度和转角的方向与虚加力的方向一致13.11.图示刚架各杆的的EI相等。试求A的位移和截面C的转角。a+国(a)解:(a)应用莫尔定理(1)刚架各段的弯矩方程M(x)=PxM(x)=0 M(x)=Pb(2)在A处垂直方向作用单位集中力t!国M(x)=0 M(x2)=x2M(x)=aA的垂直位移上海理工大学力学教研室
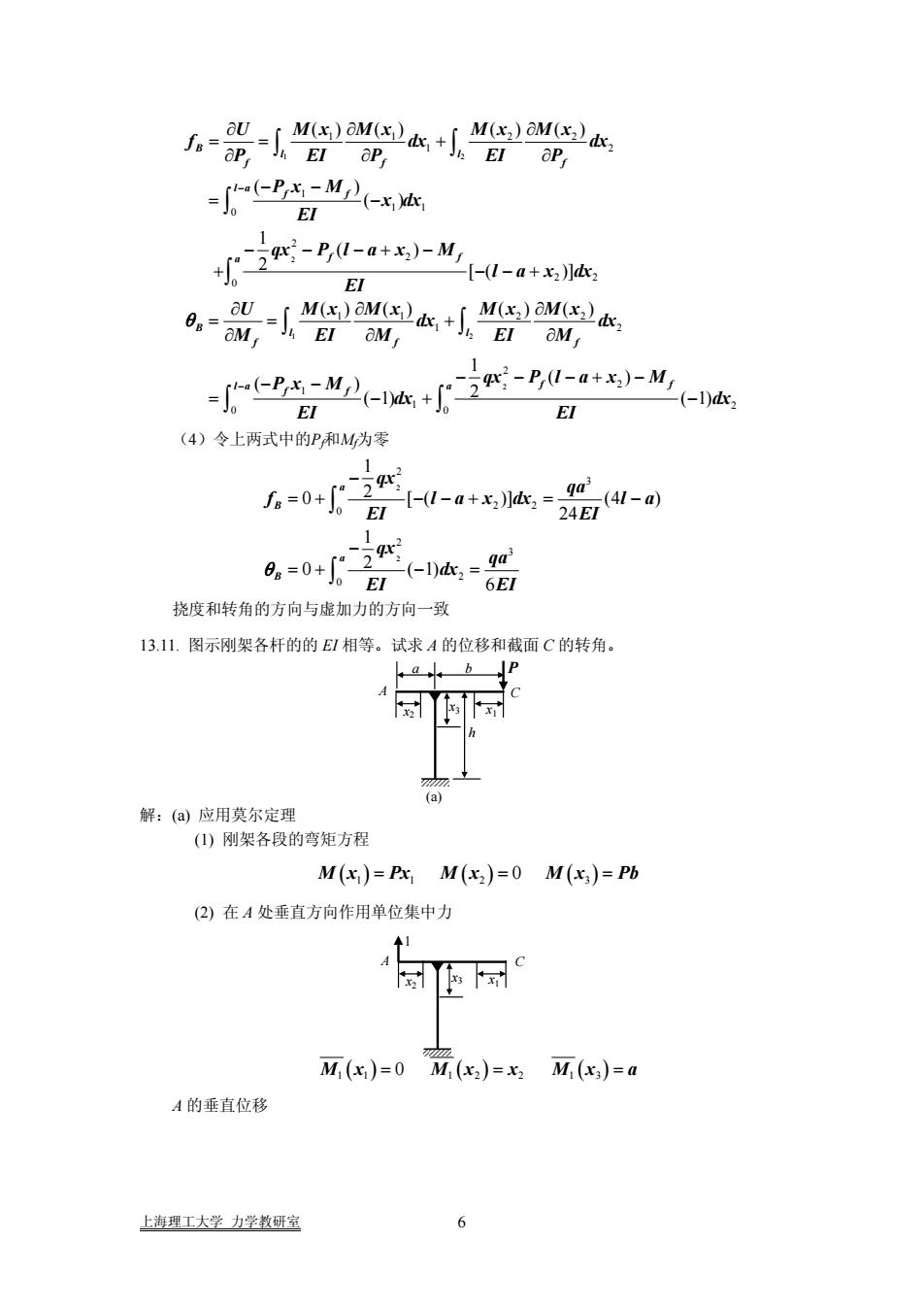
1 2 2 1 2 1 1 2 2 1 2 1 1 1 0 2 2 2 2 0 1 1 2 2 1 2 1 1 0 () () () () ( ) ( ) 1 ( ) 2 [ ( )] () () () () ( ) ( 1) B l l ff f l a f f a f f B l l ff f l a f f U Mx Mx Mx Mx f dx dx P EI P EI P Px M x dx EI qx P l a x M l a x dx EI U Mx Mx Mx Mx dx dx M EI M EI M Px M dx EI θ − − ∂∂ ∂ = = + ∂∂ ∂ − − = − − − −+ − + − − + ∂∂ ∂ = = + ∂∂ ∂ − − = − ∫ ∫ ∫ ∫ ∫ ∫ ∫ 2 2 2 2 0 1 ( ) 2 ( 1) a f f qx P l a x M dx EI − − −+ − + − ∫ (4)令上两式中的Pf和Mf为零 2 2 2 3 2 2 0 2 3 2 0 1 2 0 [( )] (4 24 1 2 0 (1) 6 a B a B qx qa f l a x dx l a) EI EI qx qa dx EI EI θ − =+ −−+ = − − =+ − = ∫ ∫ 挠度和转角的方向与虚加力的方向一致 13.11. 图示刚架各杆的的 EI 相等。试求 A 的位移和截面 C 的转角。 A C a b h x2 x1 x3 P (a) 解:(a) 应用莫尔定理 (1) 刚架各段的弯矩方程 M x Px M x M x Pb ( ) 11 2 3 = = 0 ( ) ( ) = (2) 在 A 处垂直方向作用单位集中力 1 Mx Mx x Mx a 1 1 ( ) == = 0 12 2 13 ( ) ( ) A C x2 x1 x3 A 的垂直位移 上海理工大学 力学教研室 6