
当t=0,x=-1,y=-1时,得到 xy=1 这就是1=0时刻,通过点A(L,-)的流线。它为一等变双曲线,在第三象限,如图34 所示。 图34 三、流管与流束 流管在流场中任取一非流线又不相交的封闭曲线,过曲线上各点作流线,这些流线组 成一个封闭的管状曲面,称为流管,如图35所示。由流线的定义可知,位于流管表面上得 流体质点只具有切于流管方向的速度,因而流体质点只能在流管内部或流管表面流动,而不 能穿越流管。流管如同真实的固体管壁,将其内部的流体限制在管内流动。自来水管的内表 面就是流管的一个实例。 图35所示 流束流管内的全部流体,称为流束。 微小的封闭曲线构成的流管内的流体称为元流,又称微元流束。元流的极限就是流线。 实际工程中,把管内流动和渠道中的流动看作是总的流束,它由无限多元流组成,称为 总流。 四、过流断面、湿周、水力半径、当量直径 过流断面与流束或总流的所有流线都相垂直的横断面称为过流断面。过流断面可能是平 面,也可能是各种形式的曲面,如图36所示。如果流体是水,称为过水断面。由于元流的 过流断面无限小,可以认为其断面上的运动参数分布均匀,但对于总流,过流断面上各点的 运动要素却不一定相等。 图3-6 湿周在总流的过流断面上,与流体相接触的周体边壁周长称为湿周,用x表示。 水力半径总流的过流断面面积与湿周的比值称为水力半径,用R表示。 R=4 当量直径总流过流断面面积的四倍与湿周的比值称为当量直径,用d。表示。 6
6 当 t = 0, x = −1, y = −1 时,得到 xy = 1 这就是 t = 0 时刻,通过点 A(-1,-1)的流线。它为一等变双曲线,在第三象限,如图 3-4 所示。 图 3-4 三、流管与流束 流管 在流场中任取一非流线又不相交的封闭曲线,过曲线上各点作流线,这些流线组 成一个封闭的管状曲面,称为流管,如图 3-5 所示。由流线的定义可知,位于流管表面上得 流体质点只具有切于流管方向的速度,因而流体质点只能在流管内部或流管表面流动,而不 能穿越流管。流管如同真实的固体管壁,将其内部的流体限制在管内流动。自来水管的内表 面就是流管的一个实例。 图 3-5 所示 流束 流管内的全部流体,称为流束。 微小的封闭曲线构成的流管内的流体称为元流,又称微元流束。元流的极限就是流线。 实际工程中,把管内流动和渠道中的流动看作是总的流束,它由无限多元流组成,称为 总流。 四、过流断面、湿周、水力半径、当量直径 过流断面 与流束或总流的所有流线都相垂直的横断面称为过流断面。过流断面可能是平 面,也可能是各种形式的曲面,如图 3-6 所示。如果流体是水,称为过水断面。由于元流的 过流断面无限小,可以认为其断面上的运动参数分布均匀,但对于总流,过流断面上各点的 运动要素却不一定相等。 图 3-6 湿周 在总流的过流断面上,与流体相接触的固体边壁周长称为湿周,用 表示。 水力半径 总流的过流断面面积与湿周的比值称为水力半径,用 R 表示。 A R = 当量直径 总流过流断面面积的四倍与湿周的比值称为当量直径,用 e d 表示。 A de 4 =
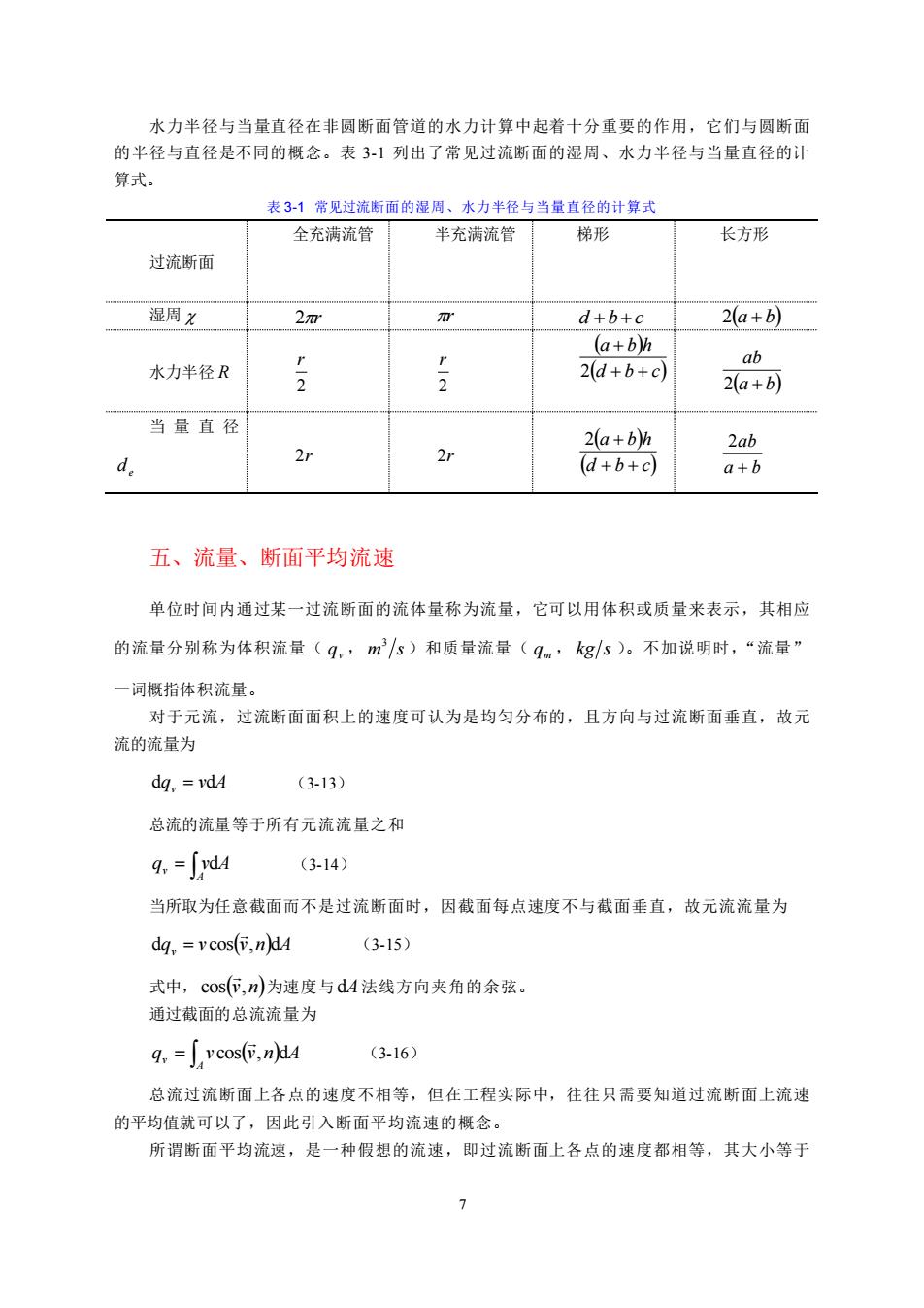
水力半轻与当量直径在非圆断面管道的水力计算中起若十分重要的作用,它们与圆断面 的半径与直径是不同的概念。表3列出了常见过流断面的湿周、水力半径与当量直径的计 算式。 表31常见过流断面的湿周、水力半径与当量直径的计算式 全充满流管 半充满流管 梯形 长方形 过流断面 湿周 2m d+b+c 2a+b) (a+bh ab 水力半径R r-2 2(d+b+c) 2(a+b) 当量直径 2r 2(a+b)h 2r 2ab (d+b+c) a+b 五、流量、断面平均流速 单位时间内通过某一过流断面的流体量称为流量,它可以用体积或质量米表示,其相应 的流量分别称为体积流量(q。,ms)和质量流量(q,kg小s)。不加说明时,“流量” ~词概指体积流量。 对于元流,过流断面面积上的速度可认为是均匀分布的,且方向与过流断面垂直,故元 流的流量为 dq,=vd4 (3-13) 总流的流量等于所有元流流量之和 9。=d4 (3-14) 当所取为任意截面而不是过流断面时,因截面每点速度不与藏截面垂直,故元流流量为 dq,vcos(v,ndA (3-15) 式中,cos(位,n)为速度与d4法线方向夹角的余弦。 通过截面的总流流量为 q.=vcos(v,n4 (3-16) 总流过流断面上各点的速度不相等,但在工程实际中,往往只需要知道过流断面上流速 的平均值就可以了,因此引入断面平均流速的概念。 所谓断面平均流速,是一种假想的流速,即过流断面上各点的速度都相等,其大小等于
7 水力半径与当量直径在非圆断面管道的水力计算中起着十分重要的作用,它们与圆断面 的半径与直径是不同的概念。表 3-1 列出了常见过流断面的湿周、水力半径与当量直径的计 算式。 表 3-1 常见过流断面的湿周、水力半径与当量直径的计算式 过流断面 全充满流管 半充满流管 梯形 长方形 湿周 2r r d +b + c 2(a + b) 水力半径 R 2 r 2 r ( ) (d b c) a b h + + + 2 (a b) ab 2 + 当量直径 e d 2r 2r ( ) (d b c) a b h + + 2 + a b ab + 2 五、流量、断面平均流速 单位时间内通过某一过流断面的流体量称为流量,它可以用体积或质量来表示,其相应 的流量分别称为体积流量( v q , m s 3 )和质量流量( m q , kg s )。不加说明时,“流量” 一词概指体积流量。 对于元流,过流断面面积上的速度可认为是均匀分布的,且方向与过流断面垂直,故元 流的流量为 dqv = vdA (3-13) 总流的流量等于所有元流流量之和 = A qv vdA (3-14) 当所取为任意截面而不是过流断面时,因截面每点速度不与截面垂直,故元流流量为 dqv v cos(v,n)dA = (3-15) 式中, cos(v,n) 为速度与 dA 法线方向夹角的余弦。 通过截面的总流流量为 ( ) = A qv v cos v,n dA (3-16) 总流过流断面上各点的速度不相等,但在工程实际中,往往只需要知道过流断面上流速 的平均值就可以了,因此引入断面平均流速的概念。 所谓断面平均流速,是一种假想的流速,即过流断面上各点的速度都相等,其大小等于

过流断面的流量q,除以过流断面面积A,即 v-2-Lu (3-17) 断面平均流速的概念十分重婴,它将使我们的研究和计算大为简化,尤其在工程计算中 具有重要的实际意义。 六、一元、二元、三元流动 根据决定流体运动参数所需的空间坐标的个数,可把流体流动分为一元流动、二元流动 和三元流动。实际流体力学问题,流动参数为三个坐标的函数,为三元流动。随着计算技术 的发展,对一些复杂问题的求解已成为可能,但对于大多数三元流动问题,研究分析通常十 分复杂。为此,在流体力学的研究和实际工程技术中,人们往往根据具体问题的性质把它简 化为二元甚至一元流动来处理。流动参数可表示为两个坐标的函数,称为二元流动。流动参 数只是一个空间坐标函数,称为一元流动。在工程流体力学中,经常引入断面平均流速的概 念,运用一元流动分析方法来解决管道与渠道中的很多流动问题。 七、均匀流动与非均匀流动 按各点运动要素(主要是速度)是否随位置而变化,可将流动分为均匀流动和非均匀流 动。流场中,在给定的某一时刻,各点速度都不随位置而变化的流动称为均匀流动。反之, 称为非均匀流动。均匀流动的所有流线都是平行直线,过流断面是一平面,且大小和形状都 沿程不变。非均匀流动的所有流线不是一组平行直线,过流断面不是一平面,且其大小或形 状沿程改变。例如,流体在等径长直管道内的流动,或在断面不变的长直渠道中的流动,都 是均匀流动。 均匀流动中,流动参数具有对空间的不变性,迁移加速度等于零。 八、渐变流与急变流 按流线沿程变化的缓急程度,又将非均匀流动分为渐变流与急变流。各流线接近于平行 直线的流动,称为渐变流。此时,各流线之间的夹角很小,且流线的曲率半径很大。反之, 称为急变流。由于渐变流的所有流线是一组几乎平行的直线,其过流断面可认为是一平面。 同时,恒定渐变流过流断面上东压强的分布近似地符合静压强的分布规律,即同一过流斯面 上:+卫÷常数。渐变流的极限情况就是均匀流。 直径沿程变化不大的圆锥管内的流动,可认为是渐变流。管径突然扩大或缩小处的流动, 可以认为是急变流。 8
8 过流断面的流量 v q 除以过流断面面积 A ,即 A vdA A q v v A = = (3-17) 断面平均流速的概念十分重要,它将使我们的研究和计算大为简化,尤其在工程计算中, 具有重要的实际意义。 六、一元、二元、三元流动 根据决定流体运动参数所需的空间坐标的个数,可把流体流动分为一元流动、二元流动 和三元流动。实际流体力学问题,流动参数为三个坐标的函数,为三元流动。随着计算技术 的发展,对一些复杂问题的求解已成为可能,但对于大多数三元流动问题,研究分析通常十 分复杂。为此,在流体力学的研究和实际工程技术中,人们往往根据具体问题的性质把它简 化为二元甚至一元流动来处理。流动参数可表示为两个坐标的函数,称为二元流动。流动参 数只是一个空间坐标函数,称为一元流动。在工程流体力学中,经常引入断面平均流速的概 念,运用一元流动分析方法来解决管道与渠道中的很多流动问题。 七、均匀流动与非均匀流动 按各点运动要素(主要是速度)是否随位置而变化,可将流动分为均匀流动和非均匀流 动。流场中,在给定的某一时刻,各点速度都不随位置而变化的流动称为均匀流动。反之, 称为非均匀流动。均匀流动的所有流线都是平行直线,过流断面是一平面,且大小和形状都 沿程不变。非均匀流动的所有流线不是一组平行直线,过流断面不是一平面,且其大小或形 状沿程改变。例如,流体在等径长直管道内的流动,或在断面不变的长直渠道中的流动,都 是均匀流动。 均匀流动中,流动参数具有对空间的不变性,迁移加速度等于零。 八、渐变流与急变流 按流线沿程变化的缓急程度,又将非均匀流动分为渐变流与急变流。各流线接近于平行 直线的流动,称为渐变流。此时,各流线之间的夹角很小,且流线的曲率半径很大。反之, 称为急变流。由于渐变流的所有流线是一组几乎平行的直线,其过流断面可认为是一平面。 同时,恒定渐变流过流断面上东压强的分布近似地符合静压强的分布规律,即同一过流断面 上 + g p z 常数。渐变流的极限情况就是均匀流。 直径沿程变化不大的圆锥管内的流动,可认为是渐变流。管径突然扩大或缩小处的流动, 可以认为是急变流

第三节连续性方程 连续性方程是质量守恒定律在流体力学中的具体体现,实质上是质量守恒方程。 一、积分形式的连续性方程 在流场中取任意形状的一个控制体,如图37所示,设其体积为V,表面积为A,n为 微元面积外法线方向上的单位矢量。 图37 任何瞬时连续充清于控制体内的流体质量可以用微元质量的体积分表示为∬P业。 经过单位时间,如果控制体内的流体质量发生了变化,则单位时间内的变化量可表示为 会(P).单位时同内,通进拉制面流入或流出拉制体的质甚之和为 f月,pvdA. 根据质量守恒定律,控制体内的质量发生变化的唯一原因就是经过控制面的流动,即单 位时间内控制体质量的变化量等于通过控制面流入或流出控制体的质量之和。也就是说,控 制体中质量的增加必然等于同一时间内流入与流出的质量差。反之,控制体中质量的减少必 然等于动一时间内流出于流入的质量差。因而有 f乐,pvdA=-84G 这就是积分形式的连续性方程。 二、微分形式的连续性方程 利用高斯定理,可将对面积的曲面积分,转化为三重体积分,即得 月pvdA=f,pm,dd止+pm,drd+pm.drd) -a()(ydz (319) y 根据控制体与时间无关的特性,可将合以,r先对控制体积分后对时间微分的次序 颠倒,则得 arfd ()-fdvddyd
9 第三节 连续性方程 连续性方程是质量守恒定律在流体力学中的具体体现,实质上是质量守恒方程。 一、积分形式的连续性方程 在流场中取任意形状的一个控制体,如图 3-7 所示,设其体积为 V ,表面积为 A , n 为 微元面积外法线方向上的单位矢量。 图 3-7 任何瞬时连续充满于控制体内的流体质量可以用微元质量的体积分表示为 V dV 。 经过单位时间,如果控制体内的流体质量发生了变化,则单位时间内的变化量可表示为 ( ) V V t d 。 单 位 时 间 内 , 通 过 控 制 面 流 入 或 流 出 控 制 体 的 质 量 之 和 为 A v d A。 根据质量守恒定律,控制体内的质量发生变化的唯一原因就是经过控制面的流动,即单 位时间内控制体质量的变化量等于通过控制面流入或流出控制体的质量之和。也就是说,控 制体中质量的增加必然等于同一时间内流入与流出的质量差。反之,控制体中质量的减少必 然等于动一时间内流出于流入的质量差。因而有 = − A V A t v d A d (3-18) 这就是积分形式的连续性方程。 二、微分形式的连续性方程 利用高斯定理,可将对面积的曲面积分,转化为三重体积分,即得 ( ) ( ) ( ) ( ) d dydz d d d d d d d + + = = + + V x y z A x y z A x z v y v x v v A v y z v x z v x y (3-19) 根据控制体与时间无关的特性,可将 V V t d 先对控制体积分后对时间微分的次序 颠倒,则得 d ( d ) d d dydz = = = V V V V x t V t V t V t

(3-20) 将(319)和(3-20)代入积分形式的连续性方程式(318),即得 ma),),g+器}ad-o Ox dv 由于积分区域为可以任意选取的控制体体积,积分为零则被积函数在流场中处处为零 「a,w,e]-0san y 这就是在直角坐标下的微分形式的连续性方程。 几种特殊情形下的连续性方程如下: 恒定流动,ap/0t=0,连续性方程简化为 apv,)dv,).)=0 (3-22) y 不可压缩流体,dp/d=0,连续性方程简化为 ++是=0 (3-22) 圆柱坐标系中的连续性方程的表达式为 ee vdo)don)dpv.)o (3-23) 三、恒定不可压缩总流的连续性方程 恒定不可压缩总流的连续性方程,可通过对总流控制体积分求得。在总流控制表面中 只有两个过流断面有流体通过,如图38所示。因为出口过流断面的面积矢量与速度矢量方 向一致,而进口的则相反,考虑恒定、不可压的特性,由式(3-18)可得 月ydA=JdA2-d4=可2A2-A=0 或2A2=1A=qr (3-24) 式中,4,A,分别为总流进、出口过流断面面积,可,分别为进、出口断面平均流 速。 图3-8 上式即为恒定不可压缩总流的连续性方程。它表明流体的体积流量沿程不变,对于任意 两过流断面,其断面平均流速与过流断面面积成反比
10 (3-20) 将(3-19)和(3-20)代入积分形式的连续性方程式(3-18),即得 ( ) ( ) ( ) d dydz = 0 + + + V x y z x z t v y v x v 由于积分区域为可以任意选取的控制体体积,积分为零则被积函数在流场中处处为零, 得 ( ) ( ) ( ) = 0 + + + z t v y v x v x y z (3-21) 这就是在直角坐标下的微分形式的连续性方程。 几种特殊情形下的连续性方程如下: 恒定流动, t = 0 ,连续性方程简化为 ( ) ( ) ( ) = 0 + + z v y v x vx y z (3-22) 不可压缩流体, d dt = 0 ,连续性方程简化为 = 0 + + z v y v x vx y z (3-22) 圆柱坐标系中的连续性方程的表达式为 ( ) ( ) ( ) 0 1 1 = + + + + z v v r r v r r v t r r z (3-23) 三、恒定不可压缩总流的连续性方程 恒定不可压缩总流的连续性方程,可通过对总流控制体积分求得。在总流控制表面中, 只有两个过流断面有流体通过,如图 3-8 所示。因为出口过流断面的面积矢量与速度矢量方 向一致,而进口的则相反,考虑恒定、不可压的特性,由式(3-18)可得 d 2 d 2 1 d 1 2 2 1 1 0 2 1 = − = − = v A v A v A v A v A A A A 或 A qV v2 A2 = v1 1 = (3-24) 式中, A1, A2 分别为总流进、出口过流断面面积, 1 v , 2 v 分别为进、出口断面平均流 速。 图 3-8 上式即为恒定不可压缩总流的连续性方程。它表明流体的体积流量沿程不变,对于任意 两过流断面,其断面平均流速与过流断面面积成反比