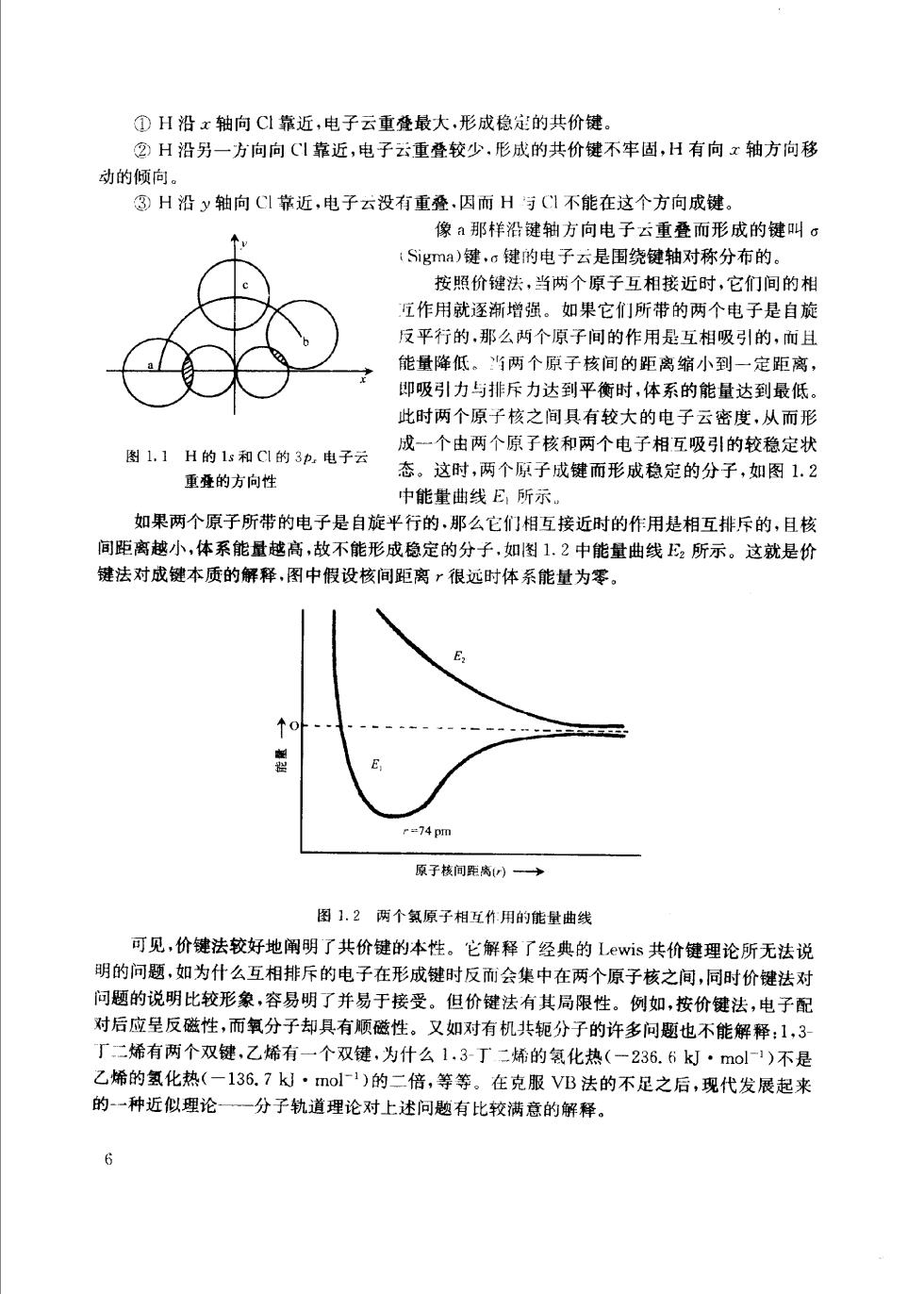
①H沿x轴向C1靠近,电子云重叠最大,形成稳定的共价键。 ②H沿另一方向向C1靠近,电子云重叠较少,形成的共价键不牢固,H有向x轴方向移 动的倾向。 ③H沿y轴向C靠近,电子云没有重叠.因而H与C不能在这个方向成键 像A那羊沿键轴方向电子云重叠而形成的键叫σ Sigma)键,w键的电子云是围绕键轴对称分布的。 按照价键法,当两个原子互相接近时,它们间的相 宜作用就逐渐增强。如果它们所带的两个电子是自旋 反平行的,那么两个原子间的作用是互相吸引的,而且 能量降低。当两个原子核间的距离缩小到一定距离, 即吸引力与排斥力达到平衡时,体系的能量达到最低 此时两个原子核之间具有较大的电子云密度,从而形 图1.1H的1和C1的3p,电子云 成一个由两个原子核和两个电子相互吸引的较稳定状 态。这时,两个原子成键而形成稳定的分子,如图1.2 重叠的方向性 中能堂曲线E所示 如果两个原子所带的电子是自旋平行的,那么它们相互接近时的作用是相互排拆的,且核 间距离越小,体系能量越高,故不能形成稳定的分子,如图1,2中能量曲线2所示。这就是价 键法对成键本质的解释,图中假设核间距离很远时体系能量为零。 =74 pm 原子核间距离一→ 图1,?两个氢原子相互作用的能量曲线 可见,价键法较好地阐明了共价键的本性。它解释了经典的Lwis共价键理论所无法说 明的问题,如为什么互相排斥的电子在形成键时反而会集中在两个原子核之间,同时价键法对 问题的说明比较形象,容易明了并易于接受。但价键法有其局限性。例如,按价键法,电子配 对后应呈反磁性,而氧分子却具有顺磁性。又如对有机共轭分子的许多问题也不能解释:1,3 丁二烯有两个双键,乙烯有一个双键,为什么1.3-丁二烯的氢化热(一236.6k·mol1)不是 乙烯的氢化热(-136.7k·mol1)的二倍,等等。在克服VB法的不足之后,现代发展起来 的一种近似理论一一分子轨道理论对上述问题有比较满意的解释

1.3.2分子轨道理论(Molecular()rbital Theory,简称M)法) 根据量子力学的观点,认为共价键可以用原子轨道的重叠形成的分子轨道来描述。原子 中电子的运动状态叫原子轨道,用薛定谔(Schrodinger)波动方程式的解一波函数中表示。 同样,所谓分子轨道,就是分子中电子的运动状态,也可用被函数来表示。分子轨道与原子 轨道相似,也有不同的能层。在基态下,分子中电子的排列从能量最低的轨道排起,按能量的 增高依次排上去(最低能量原理):电子将尽量占据最多的能级相同的分子轨道,且自旋方向相 同(洪特规侧),每个分子轨道最多只能容纳两个电子,而且自旋必须相反(鲍林原理)。两者不 同的是,原子轨道是单中心的,而分子轨道是多中心的原子轨道符号用5,d,了,.来表示, 分子轨道符号用开来表示。按照分轨道理论,有个原子轨道可以组成个分子轨道 例如氢分子轨道的波函数少可用两个H原子的1:轨道线性组合得到: 一十=有一 中,中分别表示两个氢分子轨道的波函数,中,4分别表示组成氢分子的两个氢原子的波 函数。电子波和光波、声波一样,在分子轨道中中两个波函数中,中符号相同,即位相相同,它 们将相互作用而加强,如图1.3所示 AA 图1.3符号相同的波函数因相互作用而加强 波函数加强说明两个原子核间的电子云密度增大,起者促使两个原子核结合成键的作用, 其结果是形成的分子轨道的能量较原来的原子轨道低。这样形成的分子轨道,其形状像做榄 (如图1.5所示),没有节面,称为成键轨道,以。表示。 而在分子轨道吹中,两个波函数中,中符号不同,即它们的位相不同,它们将相互作用而 减弱,如图1.4所示 图1.1符号相反的波函数因相红作用而减弱 波函数减弱说明两个原子核间的电子云密度将减小。电子云集中在两个核的外侧,把两 个核向外吸引,再加上两个原子核之间的排斥力,促使两核分离,其结果是能量较高。这样形 成的分子轨道,其形状像两个鸡蛋(两个“鸡蛋”是一个轨道),称为反键轨道,以。'表示,在反
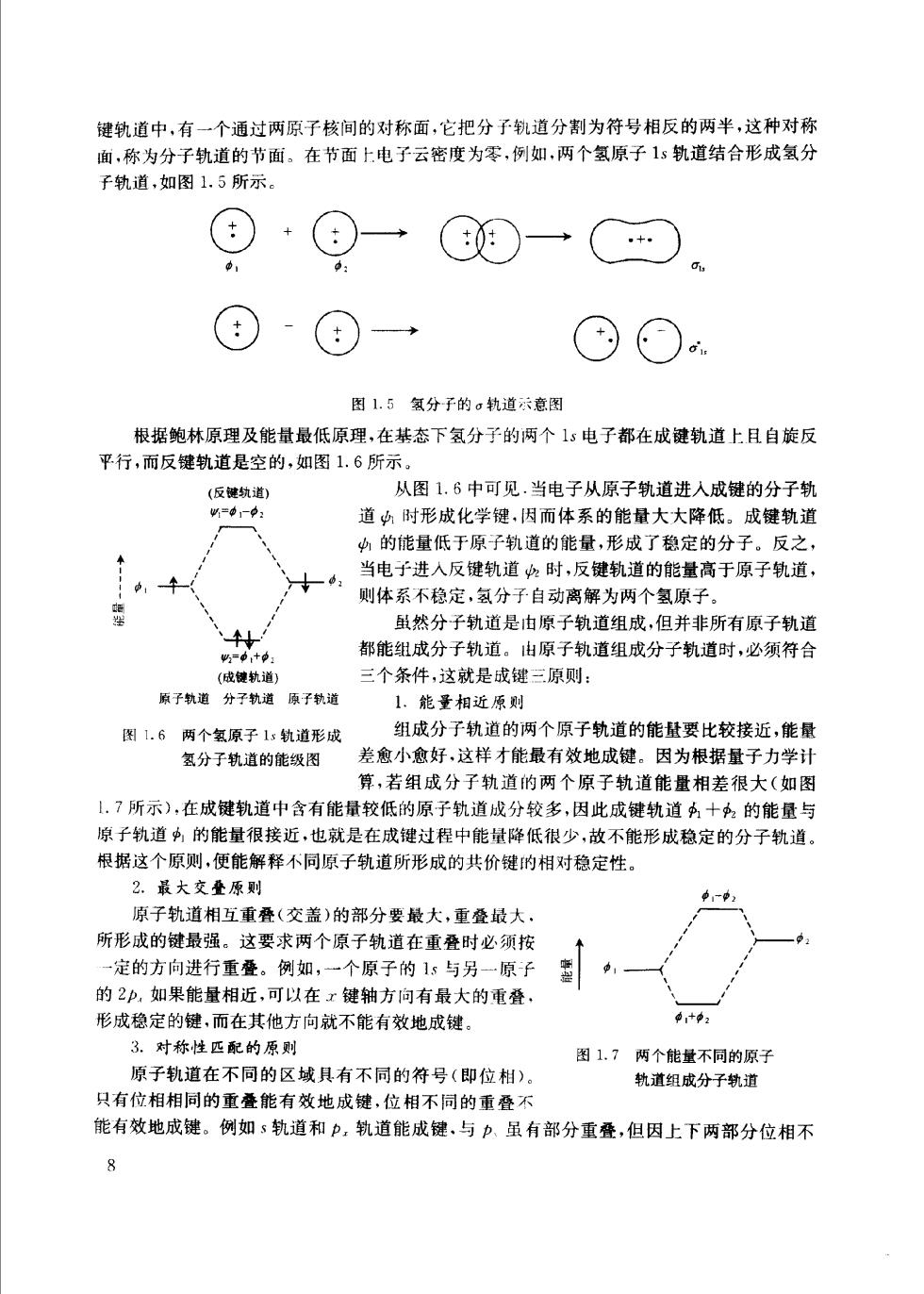
键轨道中,有一个通过两原子核间的对称面,它把分子轨道分割为符号相反的两半,这种对称 面,称为分子轨道的节面。在节面上电子云密度为零,例如,两个氢原子1s轨道结合形成氢分 子轨道,如图1.5所示 ·⊙一©0一C○ ⊙。 图1.5氢分子的。轨道示意图 根据鲍林原理及能量最低原理,在基态下氢分子的两个1s电子都在成键轨道上且自旋反 平行,而反键轨道是空的,如图1.6所示。 (反纨道〉 从图1.6中可见.当电子从原子轨道进入成键的分子轨 道中时形成化学键,因而体系的能量大大降低。成键轨道 中的能量低于原子轨道的能量,形成了稳定的分子。反之 当电于进入反键轨道时,反建轨道的能量高于原子轨道, 则体系不稳定,氢分子自动离解为两个氢原子」 虽然分子轨道是由原子轨道组成,但并非所有原子轨道 都能组成分子轨道。由原子轨道组成分子轨道时,必须符合 三个条件,这就是成键三原则: 原子轨道分子轨道原子轨道 1.能量相近原则 图1.6两个氢原子1:轨道形成 组成分子轨道的两个原子轨道的能量要比较接近,能量 氢分子轨道的能级图 差愈小愈好,这样才能最有效地成键。因为根据量子力学计 算,若组成分子轨道的两个原子轨道能量相差很大(如图 1.7所示),在成键轨道中含有能量较低的原子轨道成分较多,因此成键轨道今十2的能量与 原子轨道,的能量很接近,也就是在成键过程中能量降低很少,故不能形成稳定的分子轨道。 根据这个原则,便能解释不同原子轨道所形成的共价键的相对稳定性 2.最大交叠原则 原子轨道相互重叠(交盖)的部分要最大,重叠最大 所形成的键最强。这要求两个原子轨道在重叠时必须按 一定的方向进行重叠。例如,个原子的15与另原子 墨 的2印,如果能量相近,可以在x键轴方向有最大的重叠 形成稳定的键,而在其他方向就不能有效地成键。 3.对称性匹配的原则 图1.7两个能量不同的原子 原子轨道在不同的区域具有不同的符号(即位相)。 轨道组成分子轨道 只有位相相同的重叠能有效地成键,位相不同的重叠不 能有效地成键。例如s轨道和力,轨道能成键、与p,虽有部分重叠,但因上下两部分位相不 8
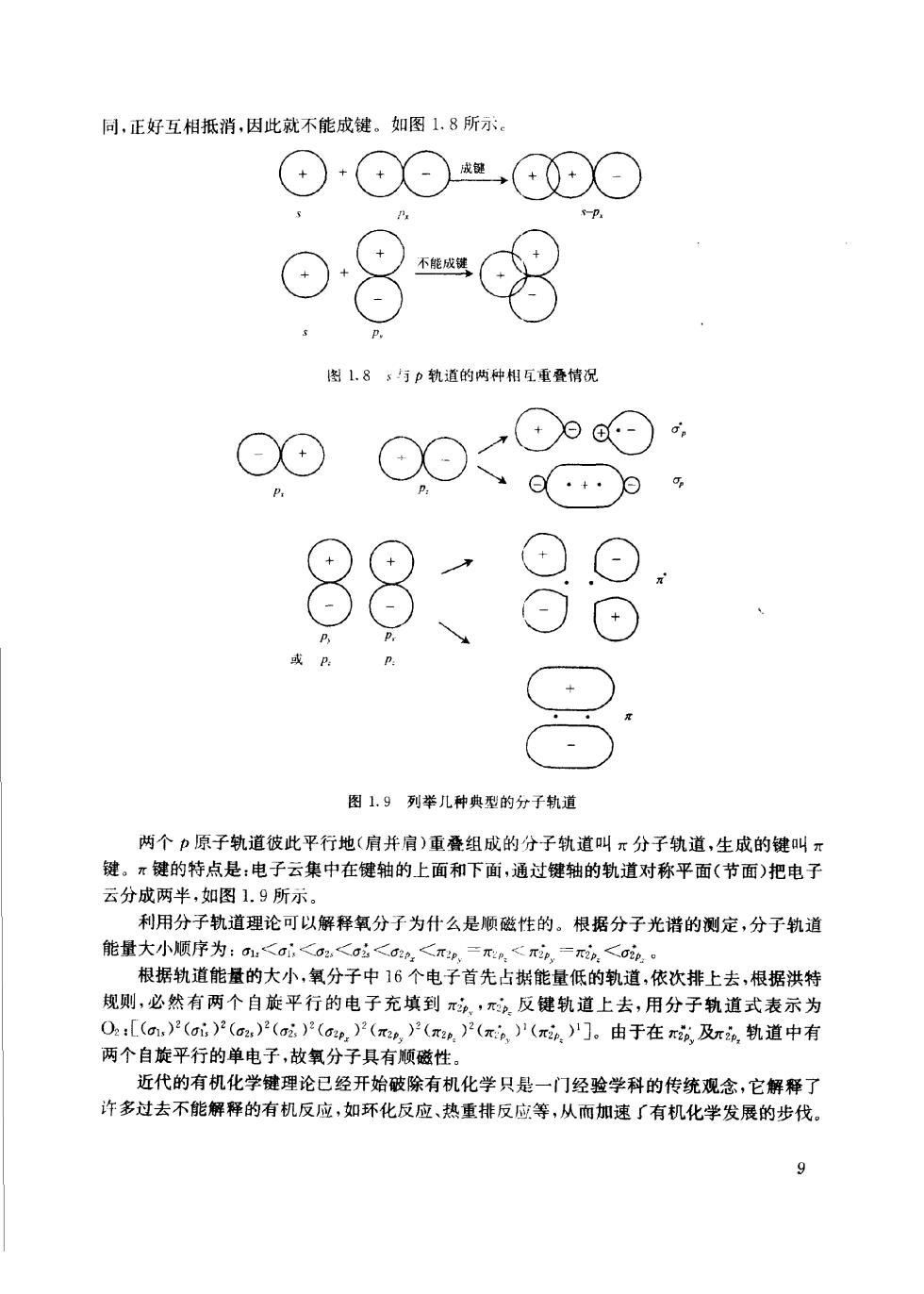
同,正好互相抵消,因此就不能成键。如图1.8所示 ⊙·⊙⊙"0⊙ o8“8 图L,8;与p轨道的两种相互重叠情况 88 )⊙ 、 或 图1.9列举儿种典型的分子轨道 两个力原子轨道彼此平行地(肩并肩)重叠组成的分子轨道叫x分子轨道,生成的键叫元 键。π键的特点是:电子云集中在键轴的上面和下面,通过键轴的轨道对称平面(节面)把电子 云分成两半,如图1.9所示。 利用分子轨道理论可以解释氧分子为什么是懒磁性的。根据分子光谱的测定,分子轨道 能量大小顺序为:<a<2<a<,<r,二<,一n<i。 根据轨道能量的大小,氧分子中16个电子首先占据能量低的轨道,依次排上去,根据洪特 规则,必然有两个自旋平行的电子充填到,.反健轨道上去,用分子轨道式表示为 0:[(am,)2(ai)2(o)2(a)(oe,)产(π,)产()2(π。)(4,)'门。由于在或及π6,轨道中有 两个自旋平行的单电子,故氧分子具有顺磁性。 近代的有机化学键理论已经开始破除有机化学只是一门经验学科的传统观念,它解释了 许多过去不能解释的有机反应,如环化反应、热重排反应等,从而加速了有机化学发展的步伐

1.3.3共振论简介 共振论是1930年代中美国加州理学院鲍林(1.Puig)提出来的一个化学理论。根据 Pauling本人说,共振论和价键法并不完全相同,它是一个经验学说,大部分是从化学实验的结 果诱导而得出的化学理论.决非是量子力学的同一领域。 现将共振论的要点叙述如下: (1)凡是一个分子(或离子)不能用单一的路易士(1wis)结构来适当地描述分子(或离 子)的电子结构时,则可用两个或多个仅在电子排列上有差别,而原子核的排列是完全相同的 结构来表示时,就存在共振。例如: 0: 甲酸离子: H-( Hc : (··是共振符号,不是平衡荷号 上面两个交替的式(i),(i)叫共振结构(reson nce structure)。从中可以看出(i)与(i)的 不同仅在于电子位置不同,而原子核的相对位置保持不变。 HC()离子的真实结构是(i),(i)两种共振结构的共振杂化体(resonance hybrid)。它 仅仅在理论上存在,因此不能离析出来。那么共振杂化体的含义是什么呢?虽然(),()中的 任何一个结构都不能很好地用来代表HC(()离子,但i),()两种结构都是参与杂化体的, 即对杂化体都有贡献。故共振结构也可以称作贡献结构(contributing structure) 有人比喻:把共振杂化体当作螺子(它是马与驴杂交生下的),骡子具有双亲的特性,但它 也有不同于双亲的自己的特性。因此,-·个共振杂化体既有每一个共振结构式的一些特性,但 是实际的杂化体又有它自已的性质。 共振杂化体常常用虚线表示部分健,即把共振杂化体想象为用实线与虚线相结合的表示 式:H-C ,这表示H(C)一中的C()不是个圳的单键和双键,而是在一个单键和一 个双健之间,即每一个CO键都其有1之的键级(bond order),同时又是等价的。 共振论的预言得到实验的证实。用X射线衍射证实HC(0离子的两个C一O键等长 127pm),介于CH,OH中的C-(O单链(143pm)和1HC-0中C-O双键(120pm)之间。 H(O0离子的氧都容纳同等的一个负电荷的),可见,共振论对于解释能够写出不止一个等 价的Lewis结构的分子或离子是特别有帮助的 (2)哪一个共振结构对共振杂化体的贡献大?上面举的例子:HC00的两个共振结构是 等价的,因此它们对杂化体的贡献是相同的,也就是说,当这些参与的各个共振结构有大约相同 的稳定性时(即具有大约相同的内能时),共振是同等重要的。每个共振结构对杂化体的参与程 度(即贡献),取决于那个共振结构的相对稳定性。共振结构越稳定,参与程度(即贡献)就越大。 例如,C可用下列共振结构式表示: 10