
7.1.3序列的运算 1.对自变量进行的运算: 移位、反褶与尺度变换 序列移位:x(n)>x(n士m) un-1) f un) 21d123n u(n+1) 2-10123 -3-2-1012n 序列反褶:Mn→Mn t(-n) 3-2-1012h
1.对自变量进行的运算: 移位、反褶与尺度变换 序列移位: x() ( ) n xn m → ± ... -2 -1 0 1 2 3 n • • 1 u n( ) .. -2 -1 0 1 2 3 n • • 1 u n( 1) − • ... -3 -2 -1 0 1 2 n • 1 u n( 1) + • 序列反褶: xn x n () ( ) → − ... -3 -2 -1 0 1 2 n • • 1 u n ( ) − 7.1.3 序列的运算
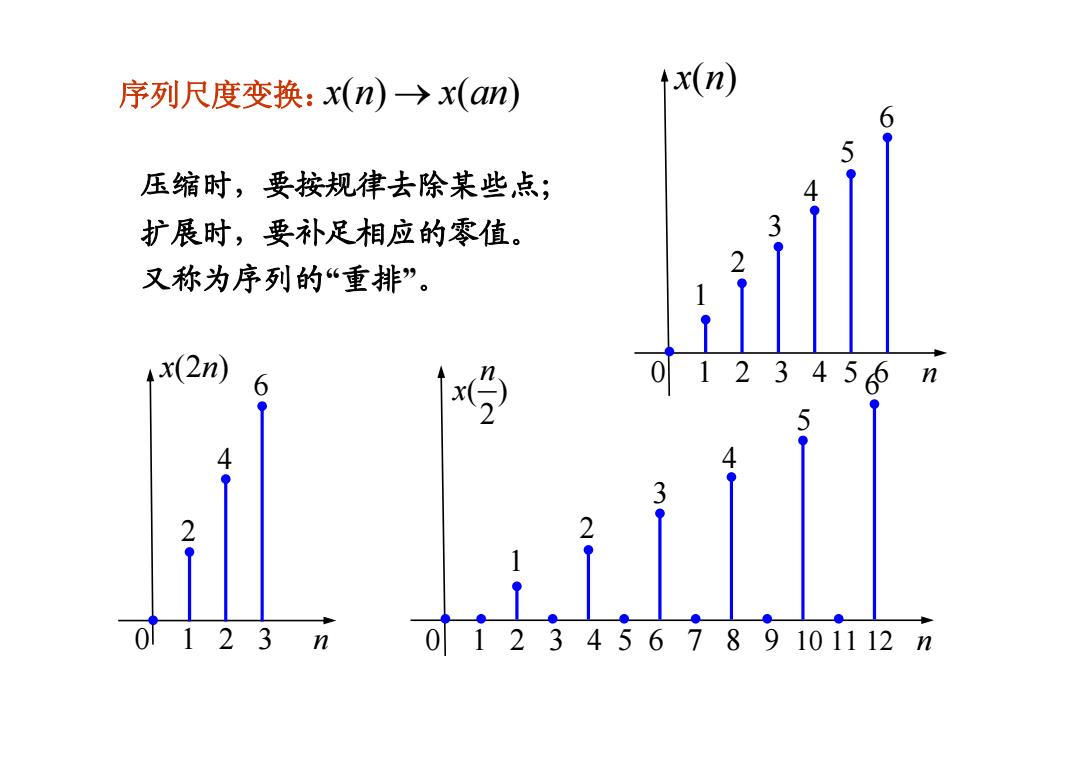
序列尺度变换:x(n)→x(an) x(n) 6 5 压缩时,要按规律去除某些点; 扩展时,要补足相应的零值。 3. 又称为序列的“重排”。 2 4x(2n) 0123455n 2● 0123 3 n 0123456789101112n
序列尺度变换:x n x an () ( ) → 0 1 2 3 4 5 6 n 1 2 3 4 5 6 x n( ) x n (2 ) 0 1 2 3 n 2 4 6 0 1 2 3 4 5 6 7 8 9 10 11 12 n ( ) 2n x 1 2 3 4 5 6 压缩时,要按规律去除某些点; 扩展时,要补足相应的零值。 又称为序列的“重排

2.对因变量进行的运算 序列相加(减):两序列同序号的数值逐项对应相加(减)。 z(n)=x(n)±y(n) 序列相乘:两序列同序号的数值逐项对应相乘。 (n)=x(n).y(n) 序列的差分:相邻两样值相减。 一阶前向差分:△x(n)=x(n+l)-x(n) 一阶后向差分:7x(n)=x(n)-x(n-1) 序列的累加: )=∑(例
z() () () n xn yn = ± 序列相加(减):两序列同序号的数值逐项对应相加(减)。 z() () () n xn yn = ⋅ 序列相乘:两序列同序号的数值逐项对应相乘。 2.对因变量进行的运算 序列的差分:相邻两样值相减。 一阶前向差分:Δx( ) ( 1) ( ) n xn xn = +− 一阶后向差分:∇xn xn xn ( ) ( ) ( 1) = −− 序列的累加: ∑ =−∞ = n m z(n) x(m)

例1:x(m=u(n) △m=什D-m=4m Vx(n)=xn)-x(n-1)=un 1) 0123n 4u(n) 中11 Vm=m-n-1)=δ(n) -10123n ↑6(n) 26=2Mm k=-0∞ ∑4(k)=(n+l)u(n)
例1: 0 1 2 3 n x() () n nu n = • 1 2 3 ... -1 0 1 2 n • • • δ ( ) n 1 ... -1 0 1 2 3 n • 1 u n( ) Δx( ) ( 1) ( ) n xn xn = +− =un( ) ( ) n k δ k =−∞ ∑ = u n( ) ( ) n k u k =−∞ ∑ = ( 1) ( ) n un + ∇un un un ( ) ( ) ( 1) = −− = δ ( ) n ∇xn xn xn ( ) ( ) ( 1) = −− =un( 1−)
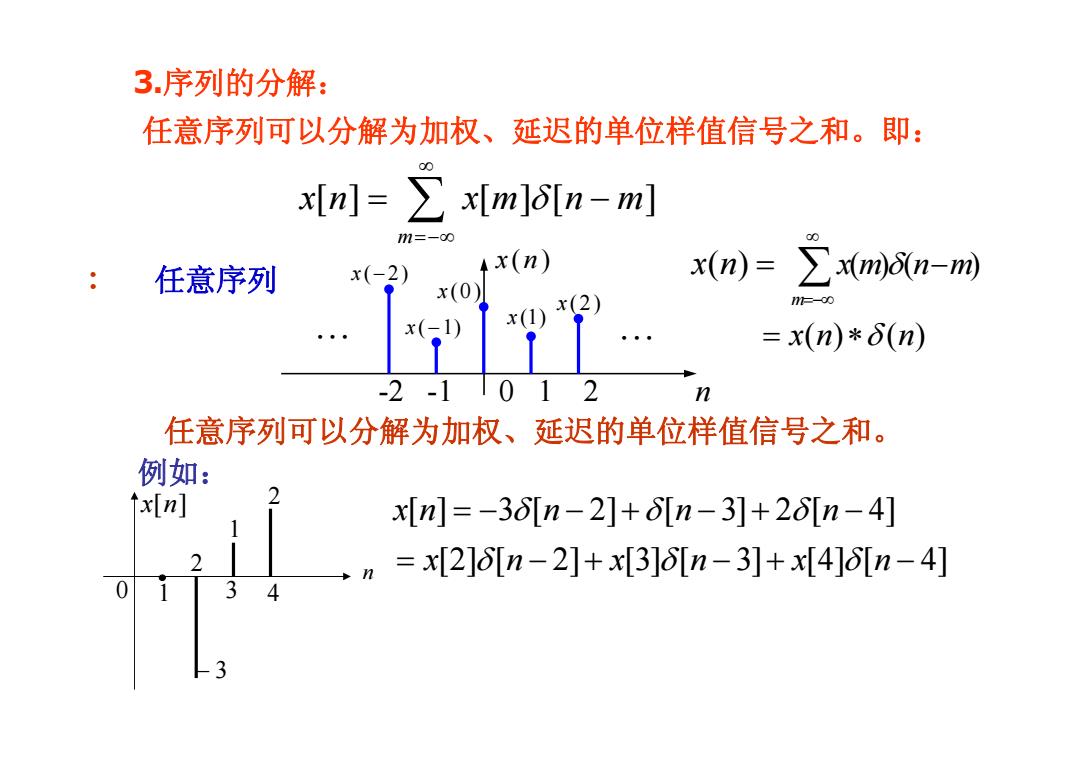
3.序列的分解: 任意序列可以分解为加权、延迟的单位样值信号之和。即: x[n=∑x[m][n-m] 1m=-o0 任意序列 x(-2) x(n) x(n)=∑m6n-m x(0) 7=-00 x(-1) x( =x(n)*δ(n) -2-11012 n 任意序列可以分解为加权、延迟的单位样值信号之和。 例如: x(n] 2 x[nm]=-3Ln-2]+Ln-3]+2[n-4] n=x[2]n-2]+x[3]6[n-3]+x[4][n-4] 0 4 3
任意序列可以分解为加权、延迟的单位样值信号之和。即: 3.序列的分解: [] [ ][ ] m x n xm n m δ ∞ =−∞ = ∑ − [ ] 3 [ 2] [ 3] 2 [ 4] [2] [ 2] [3] [ 3] [4] [ 4] xn n n n xn xn xn δ δ δ δδδ = − −+ −+ − = −+ −+ − 例如: x[ ] n n 1 2 0 3 4 1 2 − 3 任意序列可以分解为加权、延迟的单位样值信号之和。 x n( ) = ()( ) m xm n m δ ∞ =−∞ ∑ − = xn n () () ∗ δ 任意序列 ... -2 -1 0 1 2 n x ( ) n ... x (0) x (1) x (2) x ( 1) − : x ( 2) −