7.2离散时间系统的数学模型 xin] 离散系统 yn一 7.2.1LTI离散时间系统特性 x (n) H 当(n) H是线性的 K x(n)+K2x2(n) H K y(n)+K2yz(n) x,(n) H 2(n) x(n) H y(n) H是时不变的 x(n-N) H y(n-N)
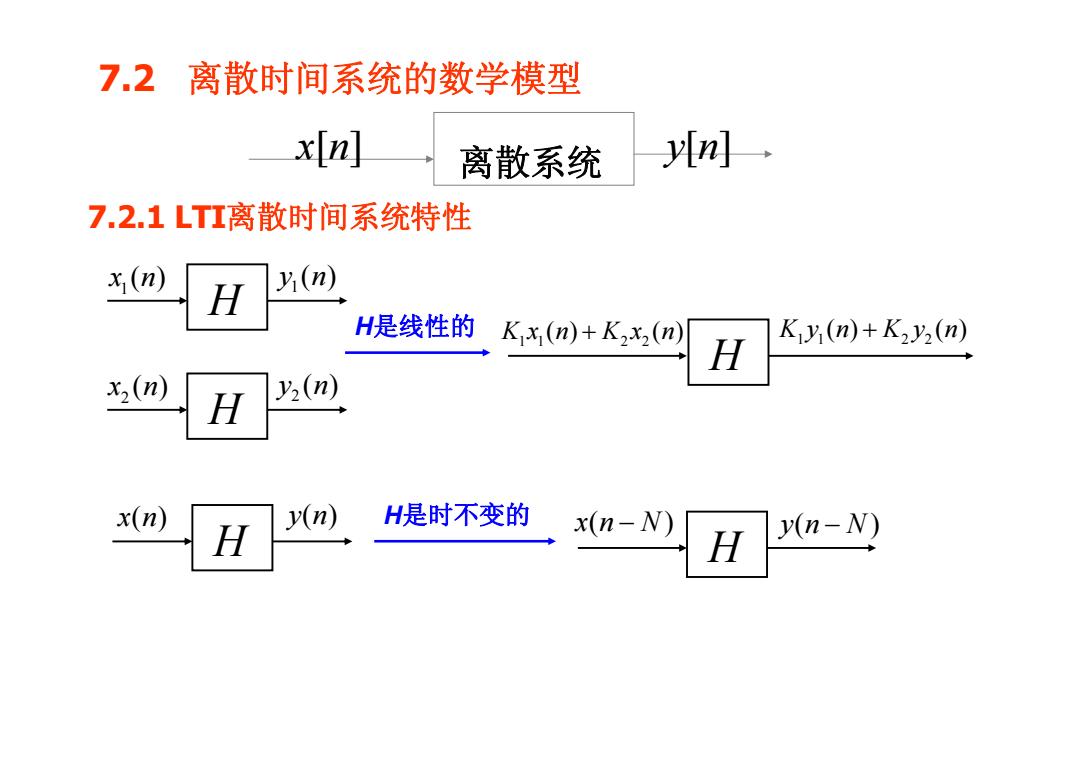
7.2 离散时间系统的数学模型 7.2.1 LTI离散时间系统特性 x[n] 离散系统 y[n] H 1 x ( ) n 1 y ( ) n H 2 x ( ) n 2 y ( ) n H是线性的 H 11 2 2 Kx n Kx n () () + 11 2 2 K y () () n K+ y n H x( ) n y( ) n H是时不变的 H x( ) n N− y( ) n N−

差分方程 7.2.2LTI离散时间系统的数学模型 (仿真框图 (1)差分方程 yn)+ayn-1)+ayn-2)..+avyn-N) =bxn)+bxn-1)+bx(n-2)..+bvxn-M) —N阶线性常系数后向差分方程 差分方程的阶数:响应y()的最大序号与最小序号之差。 y(n+2)+2y(n+1)+2y(n)=x(n+1)+2x(n) —2阶线性常系数前向差分方程
7.2.2LTI离散时间系统的数学模型 差分方程 仿真框图 —— N 阶线性常系数后向差分方程 (1)差分方程 —— 2 阶线性常系数前向差分方程 yn yn yn xn xn ( 2) 2 ( 1) 2 ( ) ( 1) 2 ( ) + + ++ = ++ 差分方程的阶数:响应 的最大序号与最小序号之差。 y n( ) ( ) ( 1) ( 2)... ( ) ( ) ( 1) ( 2)... ( ) 0 1 2 1 2 b x n b x n b x n b x n M y n a y n a y n a y n N M N = + − + − + − + − + − + −
(2)仿真框图 离散时间系统的基本运算单元:单位延时、相加、倍乘。 (a)单位延时器 (c)数乘器 x(n) ax(n) (n) 1 y(n-1) 或 a (b)加法器 x(n) ax(n) m),(②m)+4m 或 x(n) ax(n) y(n)) 例:y(n)-ay(n-l)=x(n) x(n) y(n) y(n)=x(n)+ay(n-1) a E
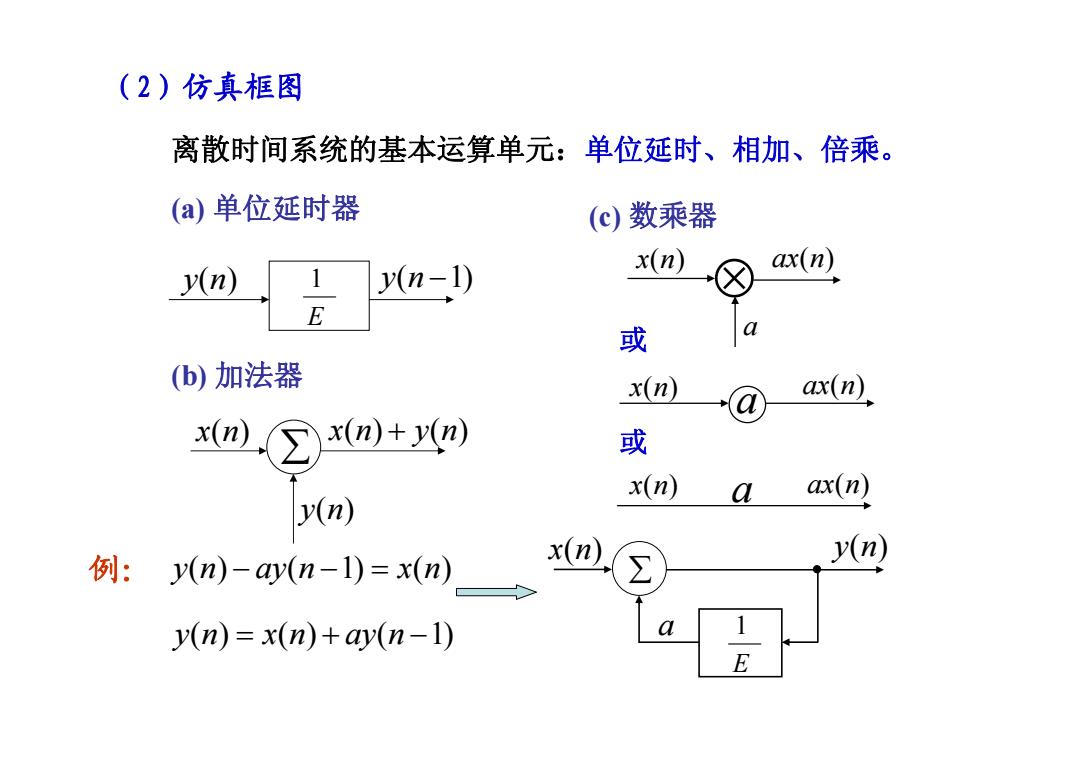
(b) 加法器 离散时间系统的基本运算单元:单位延时、相加、倍乘。 (a) 单位延时器 (c) 数乘器 (2)仿真框图 E y n( ) 1 y n( 1) − ∑ x n( ) y n( ) xn yn () () + ⊗ x( ) n a ax n( ) a x( ) n ax n( ) 或 x( ) n a ax n( ) 或 例: y n ay n x n ( ) ( 1) ( ) − −= ∑ E 1 x n( ) y n( ) a y n x n ay n ( ) ( ) ( 1) =+−
y(n) 例:已知系统框图如图 所示。求对应的数x(n) 学模型,同时画出 E E 另外一种方框图模 b, 型。 解:y(n)-by(n-l)-b2y(n-2)=ax(n)+ax(n-1) 0 q(n)-bq(n-1)-b29(n-2)=x(n) (y(n)=aog(n)+ag(n-1) an 41 y x(n) 1 E E b
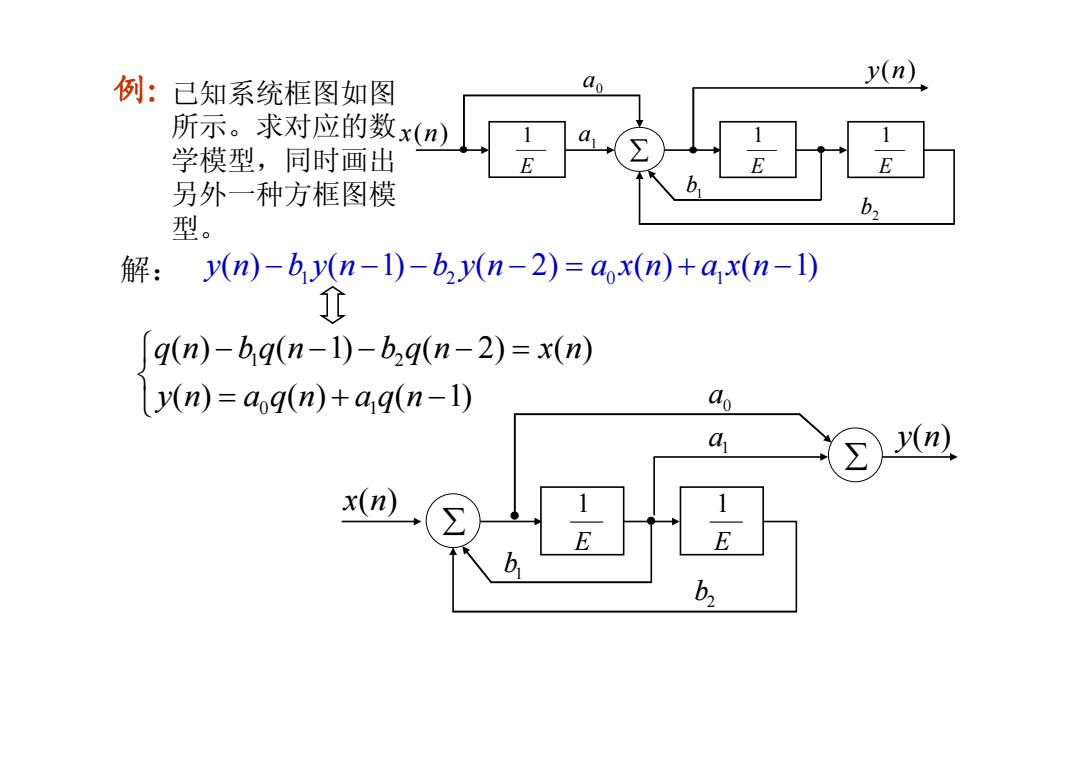
例: 1 2 01 yn byn byn axn axn ( ) ( 1) ( 2) ( ) ( 1) − −− − = + − 1 a ∑ E x( ) n 1 y n( ) E 1 E 1 0 a 1 b 2 b 1 2 0 1 ( ) ( 1) ( 2) ( ) ( ) ( ) ( 1) q n bq n bq n x n y n aq n aq n ⎧ − −− − = ⎨⎩ = +− ∑ x n( ) E1 E1 1 b 2 b 1 a y n( ) 0 a ∑ 已知系统框图如图 所示。求对应的数 学模型,同时画出 另外一种方框图模 型。 解:

例:建立下图所示系统的数学模型。 x(n] y(n] ay[n-1] a E 围绕加法器建立差分方程: y[n]=ay[n-1]+x(n] 常系数一阶后向 y[n]-ay[n-1]=x[n] 差分方程 后向差分方程:未知序列的序号自以递减的方式给出
y[ ] [ 1] [ ] n a = y n xn − + y[ ] [ 1] [ ] n a − y n xn − = 常系数一阶后向 差分方程 围绕加法器建立差分方程: 例:建立下图所示系统的数学模型。 ∑ x [ n ] a E 1 y [ n ] ay [ n-1] 后向差分方程:未知序列的序号自 n以递减的方式给出