c) (d) (e) 图65管嘴出流 流体经管嘴并且在管嘴出口断面满管流出的流动现象称为管嘴出流,管嘴出流的特点是: 当流体进入管嘴后,同样形成收缩,在收缩断面处流体与管壁分离,形成漩涡区,然后又逐 渐扩大,在管嘴出口断面上,流体完全充满整个断面。各种管嘴出流的计算方法基本相同, 本节主要讨论常见的外管嘴圆柱形管嘴出流的计算方法。 1.圆柱形外管嘴出流流量公式 圆柱形外管嘴出流分自由出流和淹没出流两种情况,下面以自由出流为例进行叙述。 1 图66(将P。改为.) 如图6-6所示,与自由出流相同,在容器内离孔口相当距离处取控制面1-1,并取管 出口断面2-2为下游控制面,以过孔口中心的水平线为基准线0-0,把断面1-1面与液面 6
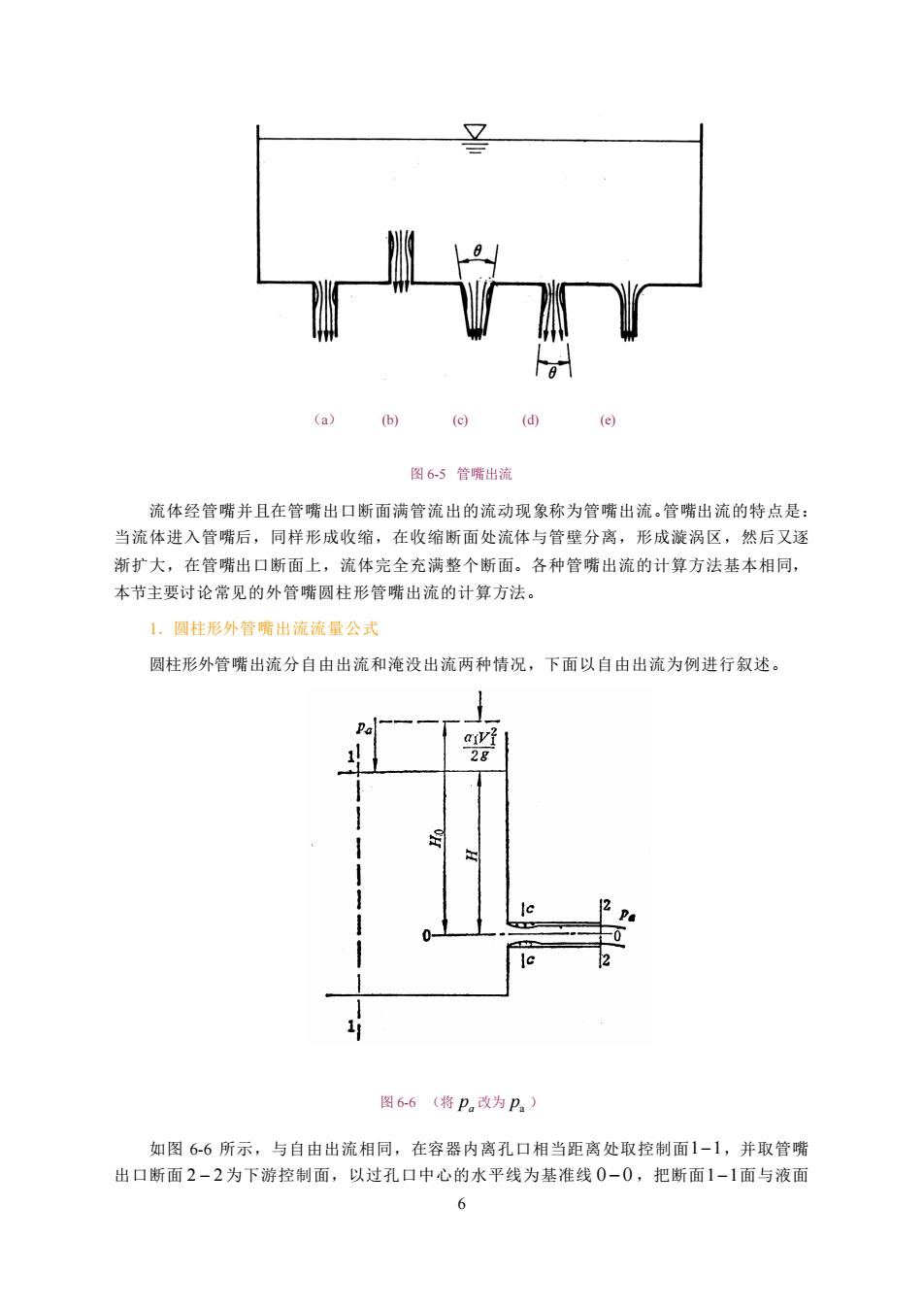
6 (a) (b) (c) (d) (e) 图 6-5 管嘴出流 流体经管嘴并且在管嘴出口断面满管流出的流动现象称为管嘴出流。管嘴出流的特点是: 当流体进入管嘴后,同样形成收缩,在收缩断面处流体与管壁分离,形成漩涡区,然后又逐 渐扩大,在管嘴出口断面上,流体完全充满整个断面。各种管嘴出流的计算方法基本相同, 本节主要讨论常见的外管嘴圆柱形管嘴出流的计算方法。 1.圆柱形外管嘴出流流量公式 圆柱形外管嘴出流分自由出流和淹没出流两种情况,下面以自由出流为例进行叙述。 图 6-6 (将 a p 改为 a p ) 如图 6-6 所示,与自由出流相同,在容器内离孔口相当距离处取控制面 1−1 ,并取管嘴 出口断面 2 − 2 为下游控制面,以过孔口中心的水平线为基准线 0 − 0 ,把断面 1−1 面与液面

交点和断面2-2与基准线0-0的交点取为控制计算点列出伯努利方程 H+号+2g-0+号+g+ (6-13) 2 2g y 式中:h2为管嘴出流的能量损失,包括液流流经孔口的局部损失和经收缩断面后突然扩大 的局部损失,以及短管的沿程损失,即 (6-14) 令瓦,=H+上,将式(6-14)代入式(6-13,整理得 2g -培6培+是+ (6-15) 因6=手,4为管嘴出口面积,4为收缩断面面积,所以5:=(任-=(:又 因%,A=4,即影=上,代入式(615,可得 -+各++盟 (6-16) V=- 1 (6-17) 管嘴出流公式为 q=3A=4V2gH。=42gH (6-18) 上式在形式上与孔口出流公式相同。当管嘴出流时,水流充满出口全部周界,因而收缩 系数等于1,故管嘴出流的流速系数等于流量系数 实验研究表明,管嘴损失系数道常趋于一稳定数值,即+(。y+入号05,而 4=10,因此=业=+05=0,82。 2.管嘴内的真空度 比较式(6-5)和式(618),在相同直径与作用水头下,管嘴的4=0.82是孔口流量系 数“=0.62的1.32倍,所以管嘴出流能力较孔口要大,在实际工程中也常用管嘴来增加出流 流量。究其原因,就是由于管嘴在收缩断面c一C处存在真空的作用。下面分析管嘴收缩断面 真空度的大小。 如图6-6所示,以收缩断面c-c和管嘴出口断面2-2分别与0-0基准线的交点为控制 计算点列伯努利方程
7 交点和断面 2 − 2 与基准线 0 − 0 的交点取为控制计算点列出伯努利方程 w1-2 2 a 2 2 2 a 1 1 2 0 2 h g p α V g p α V H + + = + + + (6-13) 式中: w1-2 h 为管嘴出流的能量损失,包括液流流经孔口的局部损失和经收缩断面后突然扩大 的局部损失,以及短管的沿程损失,即 g V d l g V g V h 2 λ 2 ζ 2 ζ 2 2 2 2 2 2 c w1-2 = 1 + + (6-14) 令 g α V H H 2 2 1 1 0 = + ,将式(6-14)代入式(6-13),整理得 g α V g V d l g V g V H 2 2 λ 2 ζ 2 ζ 2 2 2 2 2 2 2 2 2 c 0 = 1 + + + (6-15) 因 ε A c A = , A 为管嘴出口面积, A c 为收缩断面面积,所以 2 2 2 1 ε ζ 1 ε c A A − = − = ( ) ( ) ;又 因 Vc Ac = V2A ,即 2 ε c V V = ,代入式(6-15),可得 2 1 2 2 0 2 2 ζ 1 ε ( ) λ ε 2 l V H d g − = + + + (6-16) 2 0 0 1 2 2 2 1 2 2 ζ 1 ε λ ε ε V gH gH l ( ) d = = • − + + + (6-17) 管嘴出流公式为 q =V2A = A 2gH0 = A 2gH0 (6-18) 上式在形式上与孔口出流公式相同。当管嘴出流时,水流充满出口全部周界,因而收缩 系数等于 1,故管嘴出流的流速系数等于流量系数。 实验研究表明,管嘴损失系数通常趋于一稳定数值,即 1 2 2 ζ 1 ε ( ) λ 0 5 ε ε l . d − + + ,而 2 =1.0 ,因此 0.82 1 0.5 1 = + = = 。 2.管嘴内的真空度 比较式(6-5)和式(6-18),在相同直径与作用水头下,管嘴的 = 0.82 是孔口流量系 数 = 0.62 的 1.32 倍,所以管嘴出流能力较孔口要大,在实际工程中也常用管嘴来增加出流 流量。究其原因,就是由于管嘴在收缩断面 c − c 处存在真空的作用。下面分析管嘴收缩断面 真空度的大小。 如图 6-6 所示,以收缩断面 c − c 和管嘴出口断面 2 − 2 分别与 0 − 0 基准线的交点为控制 计算点列伯努利方程

号g号+ghw 式中:么收相断面后哭然扩大的月部损失,点:=飞是-(名装将前面分折结果 上=兰代入式(619,经整理得 子各-%-学]层 (6-20) 将式(6-17)代入式(6-20),可得 (6-21) y 对于圆柱形外管嘴,由实验测得ε=0.64、p=0.82。若取a。=a2=1.0,则管嘴收缩 断面的真空度为 =B-卫≈0,75 (6-22) y 上式说明管嘴收缩断面处的真空度可达作用总水头的0.75倍,相当于把管嘴的作用总水 头增加了75%。从式(6-22)可知:作用总水头H愈大,收缩断面的真空度愈大。但是当 真空度达到某一数值以上时,由于液体在低于饱和蒸汽压时将发生汽化,或空气由管嘴出口 处吸入,从而使真空破坏。根据实验结果,液流为水流、管嘴长度为(3~4)时,管嘴正常 工作的收缩断面最大真空度为7m,因此圆柱形外管嘴必须满足的条件为 A,<H,1-075*9m 3.其它常用管嘴的出流 其它类形管嘴出流的基本公式,在形式上与(617)、(618)相同,只是口和以的数值 不同。表6-2列出了几种常用的孔口和管嘴的5、£、9、4值。 例如圆锥形收缩管嘴,流速系数?值随收缩角日的增大而增大,主要是由于管内收缩后 液流扩散时的能量损失减小所致:当0=13°24'时,流量系数达到最大值4=0.946。由于它 具有较大的出口流速,所以常用于消防水枪、喷灌喷泉用喷头、冲击式水轮机喷嘴等。 圆锥形扩散管嘴出流能力取决于扩散角0和管嘴的进口形状。当0=5°~7时, 9=4=0.45~0.50:当0>8°时,由于液流的扩散角小于管嘴本身的扩散角,液流将不能 完全充满管嘴,出现类似薄壁孔口的流动状态:由于它的管嘴内具有较大的真空度和较小的 出口流速,能够将进口处的动能转化为出口处的压能,因此广泛用于流体机械、石油化工、 8
8 w 2 2 a 2 2 2 2 2 + = + + c− c c c h g p V g p V (6-19) 式中: hwc−2 收缩断面后突然扩大的局部损失, 2 2 2 2 2 wc-2 2 1 ε ζ 2 ε 2 V V h g g − = = ( ) ,将前面分析结果 2 ε c V V = 代入式(6-19),经整理得 2 a 2 2 2 2 1 ε ε ε 2 c c p p V g − − = − − ( ) (6-20) 将式(6-17)代入式(6-20),可得 a 2 2 2 2 0 1 ε ε ε c c p p H − − = − − ( ) (6-21) 对于圆柱形外管嘴,由实验测得 ε = 0.64、 = 0.82 。若取 c = 2 =1.0 ,则管嘴收缩 断面的真空度为 a 0 0.75 v c p p p H − = (6-22) 上式说明管嘴收缩断面处的真空度可达作用总水头的 0.75 倍,相当于把管嘴的作用总水 头增加了 75%。从式(6-22)可知:作用总水头 H0 愈大,收缩断面的真空度愈大。但是当 真空度达到某一数值以上时,由于液体在低于饱和蒸汽压时将发生汽化,或空气由管嘴出口 处吸入,从而使真空破坏。根据实验结果,液流为水流、管嘴长度为 (3 ~ 4)d 时,管嘴正常 工作的收缩断面最大真空度为 7m,因此圆柱形外管嘴必须满足的条件为 9 0.75 7 [ ] H0 H0 = m 3.其它常用管嘴的出流 其它类形管嘴出流的基本公式,在形式上与(6-17)、(6-18)相同,只是 和 的数值 不同。表 6-2 列出了几种常用的孔口和管嘴的 ζ 、 ε 、 、 值。 例如圆锥形收缩管嘴,流速系数 值随收缩角 的增大而增大,主要是由于管内收缩后 液流扩散时的能量损失减小所致;当 = 13 24 时,流量系数达到最大值 = 0.946 。由于它 具有较大的出口流速,所以常用于消防水枪、喷灌喷泉用喷头、冲击式水轮机喷嘴等。 圆锥形 扩散 管嘴 出流 能力 取决 于扩 散角 和管 嘴的 进口 形状 。当 = 5 ~ 7 时, = = 0.45 ~ 0.50 ;当 8 时,由于液流的扩散角小于管嘴本身的扩散角,液流将不能 完全充满管嘴,出现类似薄壁孔口的流动状态;由于它的管嘴内具有较大的真空度和较小的 出口流速,能够将进口处的动能转化为出口处的压能,因此广泛用于流体机械、石油化工
航空航天等工程领域流体喷射部件的动能回收,如喷射泵、水轮机的尾水管等。 流线形圆管嘴,由于液流在管嘴内无收缩和扩散现象,因而能量损失最小,流速系数利 流量系数均大于其它类型管嘴,一般0=“=0.98。这种管嘴常被用于水坝坝身的高速泄水 孔口,也被广泛用于各种管道的进口。 表6-2孔口的管嘴的C、£、0、u值 流量 学号 孔口、管嘴类型 意图 阻力系数( 收缩 流速 系数E 系数0 系数4 1 薄壁圆形孔口 图61 0.06 06d 0.97 062 修圆小孔口 1.00 0.98 0.98 3 圆柱形外管嘴 图6-5(a) 05 10 082 082 4 圆柱形内管塔 图6-5(b) 1.0 1.0 0.71 0.71 锥形收缩管嘴 图6-5(c 0.09 0.9 (0=12°15° 096 锥形扩管嘴 (0=5°7) 图65(d 1.0 0.45-0.50 045-0.5 流线形圆管嘴 图6-5(c 004 1.0 0.98 (圆角进口) 第二节孔口及管嘴的变水头出流 在实际工程中,还会遇到孔口(或管嘴)的变水头出流问题,如当容器的水头在孔口(或 管嘴)出流过程中增大或减小,就形成了变水头作用下的孔口(或管嘴)出流问题。变水头 出流问题属于子非恒定出流问题,但是因容器断面面积远大于孔口面积,水头变化较缓慢,惯 性力可以忽略不计,可以将每微小时段内的孔口出流认为水头不变,按孔口恒定流处理。 图6.7 图67所示为一变截面容器,容器底部开有一个薄壁小孔口,面积为A。设某瞬时1容 器内的液位为:,经过某微小时段d“,液位变化止,横截面变化面积A是坐标:的函数 A()。此时根据孔口出流计算出孔口出流的流量q=4,√2g,由水流的连续性可知,时段
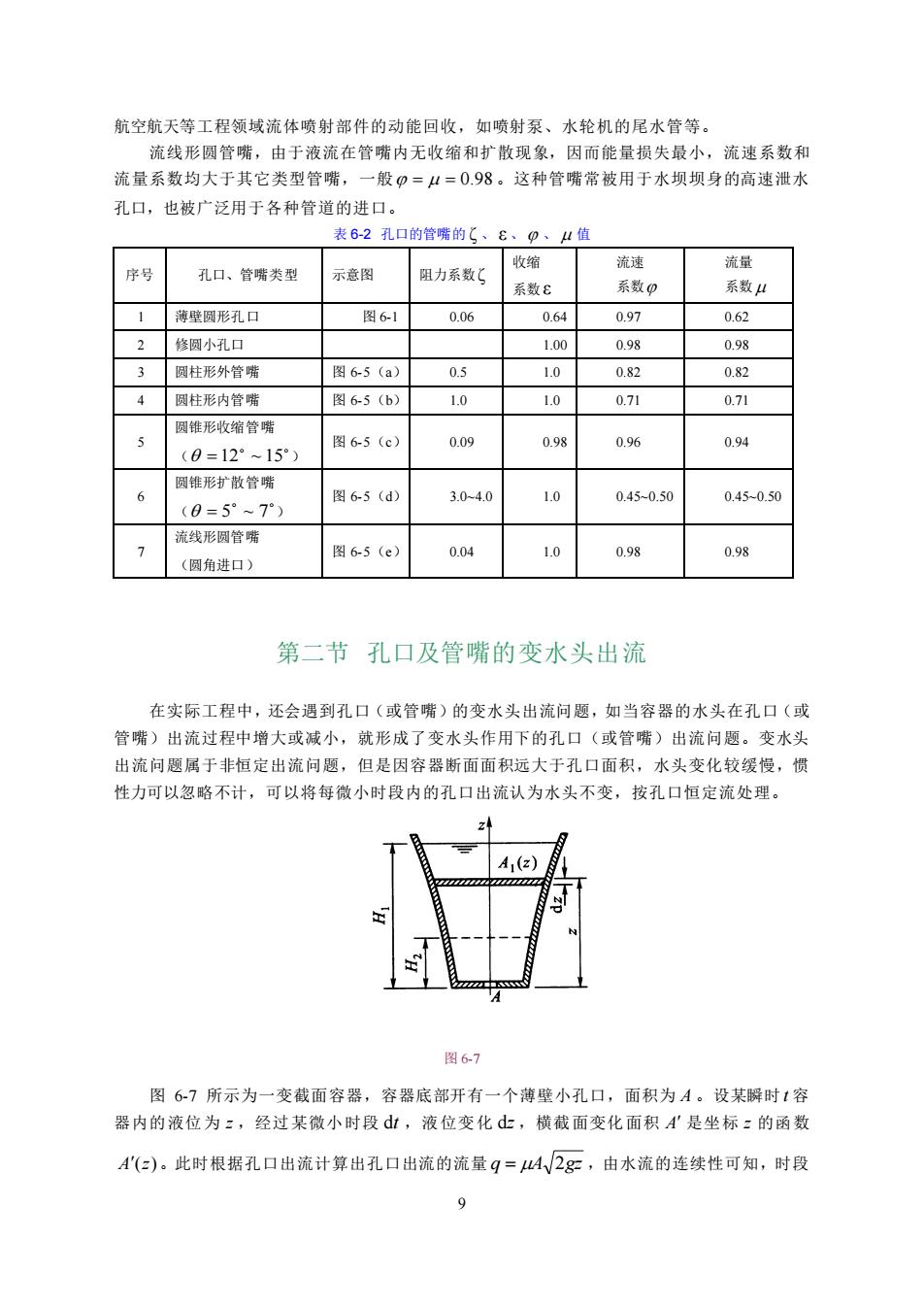
9 航空航天等工程领域流体喷射部件的动能回收,如喷射泵、水轮机的尾水管等。 流线形圆管嘴,由于液流在管嘴内无收缩和扩散现象,因而能量损失最小,流速系数和 流量系数均大于其它类型管嘴,一般 = = 0.98 。这种管嘴常被用于水坝坝身的高速泄水 孔口,也被广泛用于各种管道的进口。 表 6-2 孔口的管嘴的 ζ 、 ε 、 、 值 序号 孔口、管嘴类型 示意图 阻力系数 ζ 收缩 系数 ε 流速 系数 流量 系数 1 薄壁圆形孔口 图 6-1 0.06 0.64 0.97 0.62 2 修圆小孔口 1.00 0.98 0.98 3 圆柱形外管嘴 图 6-5(a) 0.5 1.0 0.82 0.82 4 圆柱形内管嘴 图 6-5(b) 1.0 1.0 0.71 0.71 5 圆锥形收缩管嘴 ( = 12 ~ 15 ) 图 6-5(c) 0.09 0.98 0.96 0.94 6 圆锥形扩散管嘴 ( = 5 ~ 7 ) 图 6-5(d) 3.0~4.0 1.0 0.45~0.50 0.45~0.50 7 流线形圆管嘴 (圆角进口) 图 6-5(e) 0.04 1.0 0.98 0.98 第二节 孔口及管嘴的变水头出流 在实际工程中,还会遇到孔口(或管嘴)的变水头出流问题,如当容器的水头在孔口(或 管嘴)出流过程中增大或减小,就形成了变水头作用下的孔口(或管嘴)出流问题。变水头 出流问题属于非恒定出流问题,但是因容器断面面积远大于孔口面积,水头变化较缓慢,惯 性力可以忽略不计,可以将每微小时段内的孔口出流认为水头不变,按孔口恒定流处理。 图 6-7 图 6-7 所示为一变截面容器,容器底部开有一个薄壁小孔口,面积为 A 。设某瞬时 t 容 器内的液位为 z ,经过某微小时段 dt ,液位变化 dz ,横截面变化面积 A 是坐标 z 的函数 A(z) 。此时根据孔口出流计算出孔口出流的流量 q = A 2gz ,由水流的连续性可知,时段

d!内孔口出流液体体积等于容器中液位下降的体积,即 HA 2gdt=-A(=)d= 设在1=0、【=T,液位分别为H,和H,则对上式进行定积分求出液位变化时间 T=d=- 广g4 1 对于等截面容器,A()=A。,代入上式积分得 面-面 (6-23) 如H2=0,则求得容器泄空所需时间: T-24匹.2AH=2业 (6-24) MA 2g MA2gH 9ms 式中:V为容器泄空体积:9为容器开始出流的最大流量。 可见,等截面容器中液体的泄空时间等于在初始水头作用下恒定流出相同体积所需时间 的2倍。 若容器壁上不是孔口,而是其它类型的管嘴或短管,上述推导过程和计算公式仍然适用, 只是流量系数变化而异。 第三节简单管路的水力计算 管路是组成工程实际中输送流体运动的重要组成设备,其水力计算方法与前面的孔口、 管嘴出流计算相似,只是需要同时考虑沿程水头损失和局部水头损失 在水力计算中,通常将等径、无分支管路系统称为简单管路,而将由几段不同管径、不 同长度的管段组合而成的复杂管路系统称为复杂管路。在能量损失的组成中,当局部损失和 出流的速度水头之和与其沿程损失相比较小(通常小于5%),可以忽略不计,此类的管路称 为长管,否则称为短管。如工程中离心泵压水管、远距离输水管等可认为长管,而水泵吸水 管、虹吸管与倒虹吸管等则可认为是短管。 本节主要介绍短管、长管的基本计算公式,并以虹吸管、倒虹吸管及离心泵管路系统为 为例介绍实际工程中应用。 10
10 dt 内孔口出流液体体积等于容器中液位下降的体积,即 A gz t A ( z ) z 2 d d = − 设在 t = 0、t = T ,液位分别为 H1 和 H2 ,则对上式进行定积分求出液位变化时间: 2 1 0 1 d d 2 T H H A ( z ) T t z A g z = = − 对于等截面容器, 0 A(z) = A ,代入上式积分得 ( ) 2 2 1 2 0 H H A g A T = − (6-23) 如 H2 = 0 ,则求得容器泄空所需时间: 1 max 0 1 0 1 2 2 2 2 2 q V A gH A H A g A H T = = = (6-24) 式中:V 为容器泄空体积; qmax 为容器开始出流的最大流量。 可见,等截面容器中液体的泄空时间等于在初始水头作用下恒定流出相同体积所需时间 的 2 倍。 若容器壁上不是孔口,而是其它类型的管嘴或短管,上述推导过程和计算公式仍然适用, 只是流量系数变化而异。 第三节 简单管路的水力计算 管路是组成工程实际中输送流体运动的重要组成设备,其水力计算方法与前面的孔口、 管嘴出流计算相似,只是需要同时考虑沿程水头损失和局部水头损失。 在水力计算中,通常将等径、无分支管路系统称为简单管路,而将由几段不同管径、不 同长度的管段组合而成的复杂管路系统称为复杂管路。在能量损失的组成中,当局部损失和 出流的速度水头之和与其沿程损失相比较小(通常小于 5%),可以忽略不计,此类的管路称 为长管,否则称为短管。如工程中离心泵压水管、远距离输水管等可认为长管,而水泵吸水 管、虹吸管与倒虹吸管等则可认为是短管。 本节主要介绍短管、长管的基本计算公式,并以虹吸管、倒虹吸管及离心泵管路系统为 为例介绍实际工程中应用