
应力状态与应变状态O考虑剪应力互等和三角变换,得:ar+a.0.-0,cos 2α - t, sin 2αOa-22Txy同理:图10x0x6一sin 2α + t cos2α一TaOd2aa.TarTxyVa,0x图2
x 图1 y sx txy sy O sy txy sx s t x y O t n 图2 t s s s s s cos2 sin 2 2 2 xy x y x y − − + + = t s s t sin 2 cos2 2 xy x y + − = 考虑剪应力互等和三角变换,得: 同理:
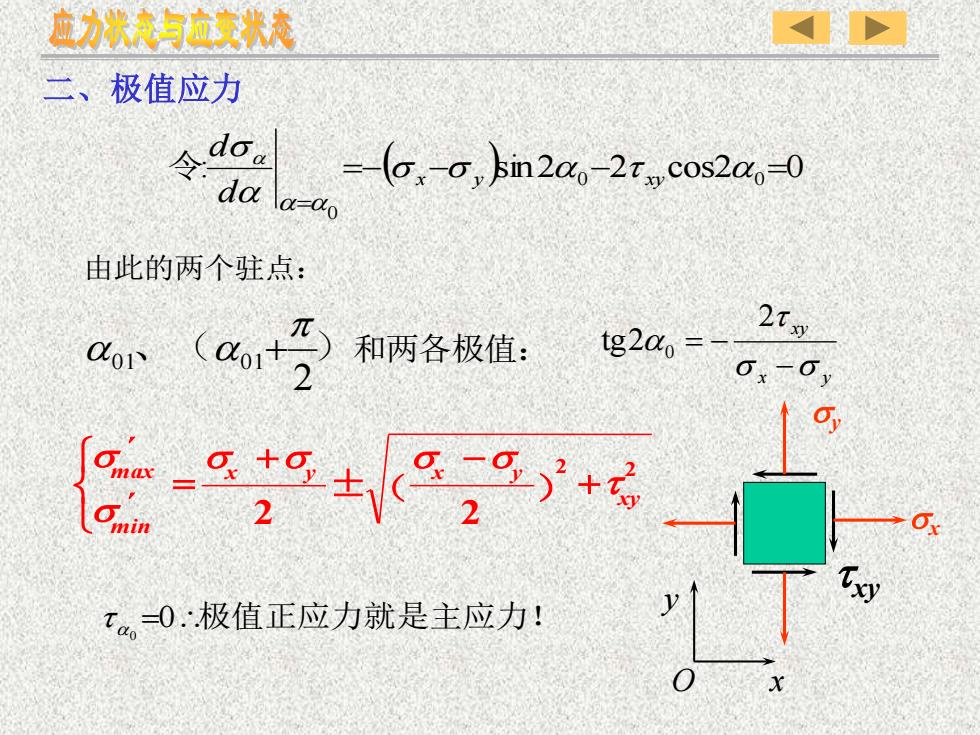
应力状态与应变状态二、极值应力Adoa--(o,α,bin20o-2t,cos20=0dαTα=o由此的两个驻点:2txy元tg2α。和两各极值:(01+αo1Ox-9.2a-at+o9aTxyt。。=0:极值正应力就是主应力!O
: ( )sin2 0 2 cos2 0 0 0 =− − − = = s s t s x y xy d d 令 二、极值应力 x y xy s s t − = − 2 、( )和两各极值: tg2 0 由此的两个驻点: 2 01 01 + t 0 =0极值正应力就是主应力! ) 2 2 2 2 xy x y x y min max t s s s s s s + − ± + = ( ´ ´ x y sx txy sy O

应力状态与应变状态O0-0mx; 05-0mn主义α"在剪应力相对的项限内,0单元体且偏向于o 及o,大的一侧。ORyAdaO0X-0tg2αf公2txdα lα=αiEe元即极值剪应力面与主面成45°α=αi +福4
x y sx txy sy O 主 s1 在剪应力相对的项限内, 单元体 且偏向于sx 及sy大的一侧。 0 d d : 1 = = t 令 xy x y t s s 2 tg2 1 − = 2 2 2 x y x y min max t s s t t + − =± ( ) 0 0 1 , 45 4 即极值剪应力面与主面 成 = + 1 max 2 min s =s ; s =s s 2 s1
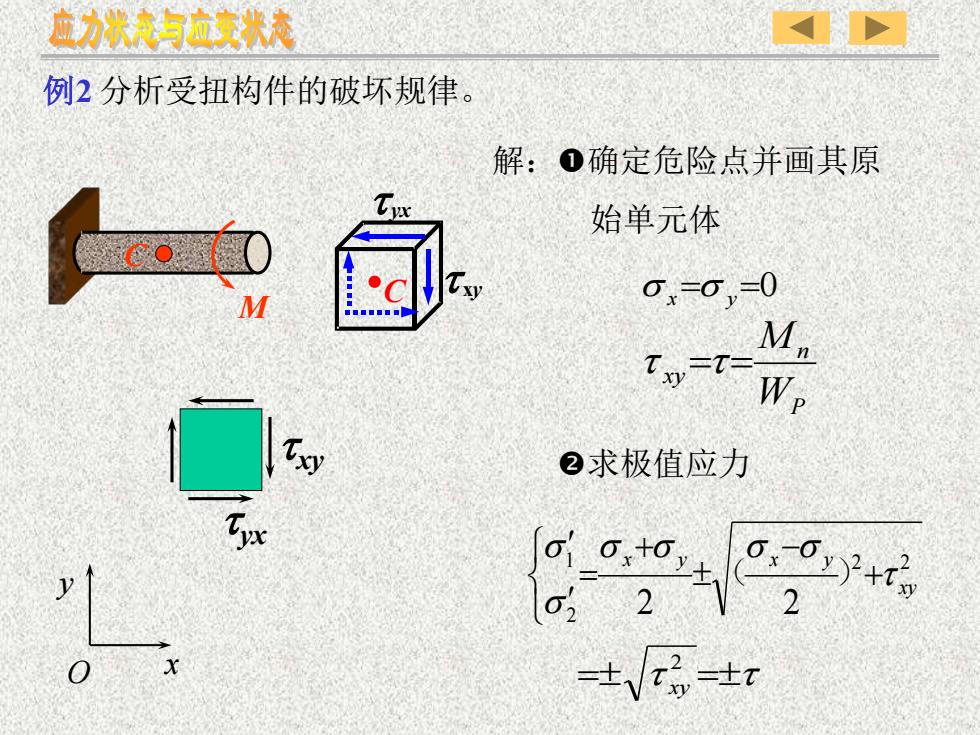
应力状态与应变状态例2分析受扭构件的破坏规律解:O确定危险点并画其原Tyx始单元体α.=o,-0MMhTxy=TW,②求极值应力ny a+aOx2+t12a,x0-±Vt,-±t
例2 分析受扭构件的破坏规律。 解:确定危险点并画其原 始单元体 求极值应力 s x =s y =0 P n xy W M t =t= 2 2 2 1 2 2 xy x y x y t s s s s s s + − + = ( ) = t =t 2 xy C t xy t yx M C x y O txy t yx
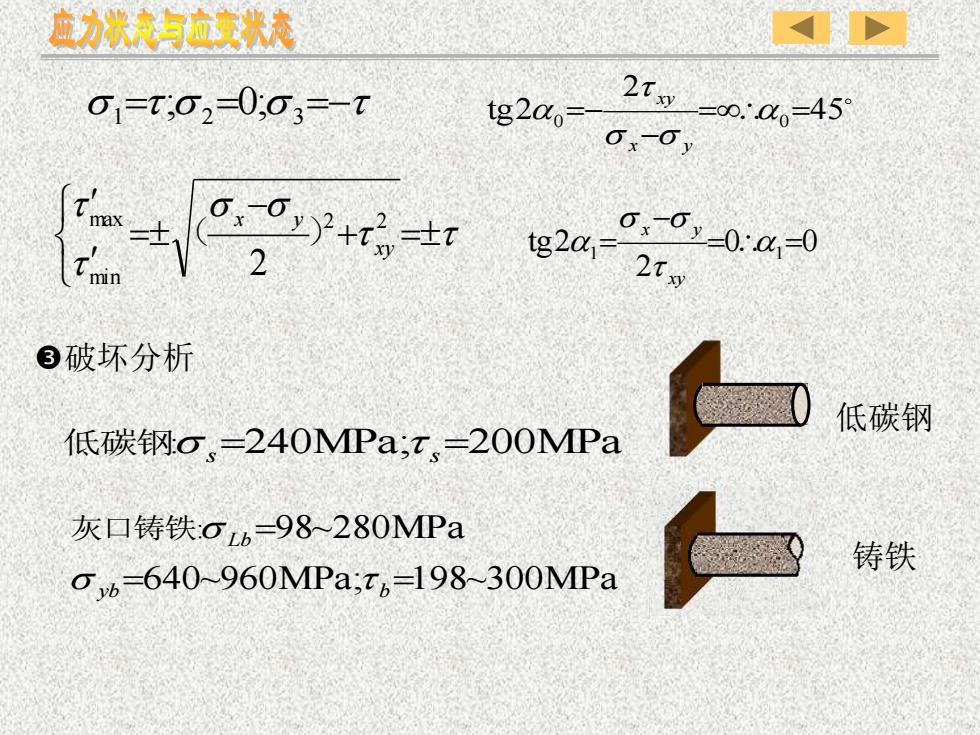
应力状态与应变状态2ty0-t,02-0,03=-T=00. .0=45°tg2α0.-o,o00,-0:α1-0tg2α,=D2txy③破坏分析低碳钢低碳钢o-240MPa;t=200MPa灰口铸铁:αh-98~280MPa铸铁O yb=640~960MPa;t,-198~300MPa
破坏分析 t t s s tt + = − = 2 2 min max 2 xy x y ( ) s =t s = s = −t 1 2 3 ; 0 ; 45 2 tg 2 0 = 0 = − = − s s t x y xy 0 0 2 tg 2 1 = 1 = − = t s s xy x y 低碳钢:s s =240MPa;t s =200MPa 640~960MPa; 198~300MPa : 98~280MPa = = = yb b Lb s t 灰口铸铁 s 低碳钢 铸铁