
材料力学第六章弯曲变形

第六章弯曲变形$ 6-1概述$6-2梁的挠曲线近似微分方程及其积分$6-3求梁的挠度与转角的共轭梁法$6-4按叠加原理求梁的挠度与转角$6-5梁的刚度校核$6-6梁内的弯曲应变能$6-7简单超静定梁的求解方法$6-8梁内的弯曲应变能
§6–1 概述 §6–2 梁的挠曲线近似微分方程及其积分 §6–3 求梁的挠度与转角的共轭梁法 §6–4 按叠加原理求梁的挠度与转角 §6–5 梁的刚度校核 第六章 弯曲变形 §6–6 梁内的弯曲应变能 §6–7 简单超静定梁的求解方法 §6–8 梁内的弯曲应变能
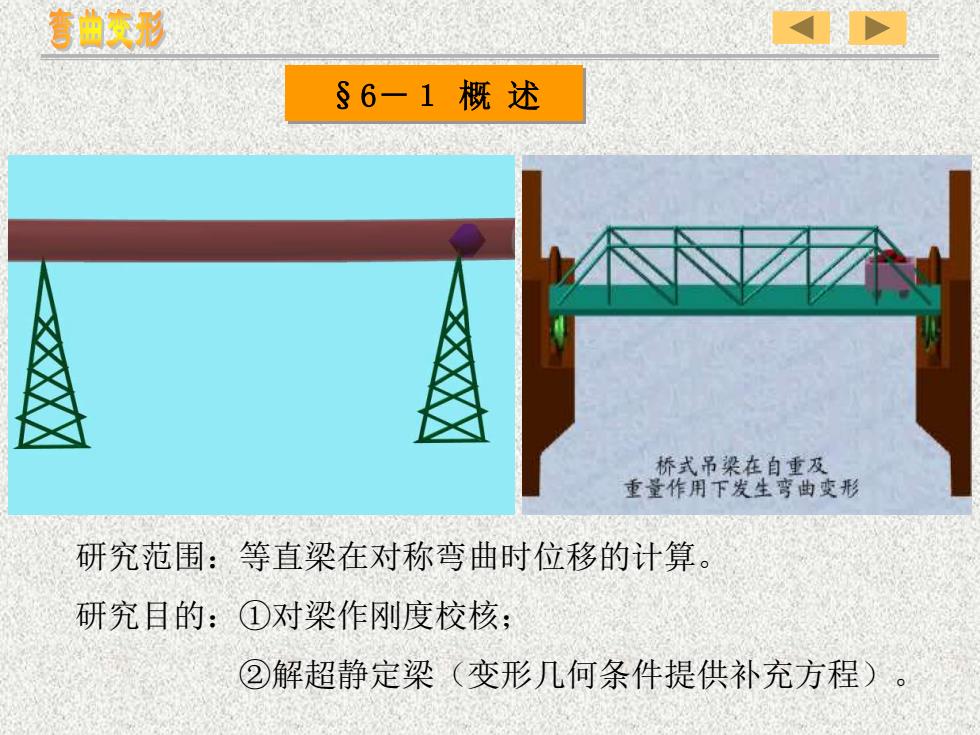
弯曲变形S6-1概述桥式吊染在自重及重量作用下发生弯曲变形研究范围:等直梁在对称弯曲时位移的计算研究目的:①对梁作刚度校核;②解超静定梁(变形几何条件提供补充方程)福
§6-1 概 述 研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核; ②解超静定梁(变形几何条件提供补充方程)

弯曲变形度量梁变形的两个基本位移量1.挠度:横截面形心沿垂直于轴线方向的线位移。用v表示。与 f同向为正,反之为负。2.转角:横截面绕其中性轴转t动的角度。用①表示,顺时针转动为正,反之为负。二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。其方程为:v=f (x)小变形df三、转角与挠曲线的关系:tgo=0=f'(1)Ddx
1.挠度:横截面形心沿垂直于轴线方向的线位移。用v表示。 与 f 同向为正,反之为负。 2.转角:横截面绕其中性轴转 动的角度。用 表示,顺时 针转动为正,反之为负。 二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。 其方程为: v =f (x) 三、转角与挠曲线的关系: 一、度量梁变形的两个基本位移量 (1) d d tg f x f = = 小变形 P x v C C1 f

弯曲变形S 6-2梁的挠曲线近似微分方程及其积分挠曲线近似微分方程AM.(x)EI.pxM>0小变形1f"(x)+± f"(x)f"(x)<0-2(1+fn)%pfM.(x). f"(x)=±XEI.M (x)M<0(2): J"(x) =-EIf"(x)>0f式(2)就是挠曲线近似微分方程
§6-2 梁的挠曲线近似微分方程及其积分 z z EI 1 M (x) = 一、挠曲线近似微分方程 z z EI M x f x ( ) ( ) = 式(2)就是挠曲线近似微分方程。 EI M x f x ( ) ( ) = − . (2) ( ) (1 ) 1 ( ) 2 3 2 f x f f x + = 小变形 f x M>0 f (x) 0 f x M<0 f (x) 0