内蒙古科技大学考试标准答案及评分标准(试卷A)课程名称:材料力学A考试班级:机械07、力学07考试时间:200年月日时分至时分标准制订人:张永红一、是非题(对的在括号内画√,错的画×)(共5题,每题2分,共10分)1.×;2.X;3.V;4.V;5.V二、选择题(共10题,每题3分,共30分)1.(b);2.(b);3.(a);4.(b);5.(a);6.(a);7.(c);8.(b);9. (b);10. (c)三、作图题(12分)解:1.求约束力F,=Fg =47kN9 =3kN/m JF=70kNAc仓4m4m邹(KN)(+)F图6分(-)164(eN-m)(t)6分M图说明:只求约束力给2分四、计算题(12分)解:1.求CD杆轴力
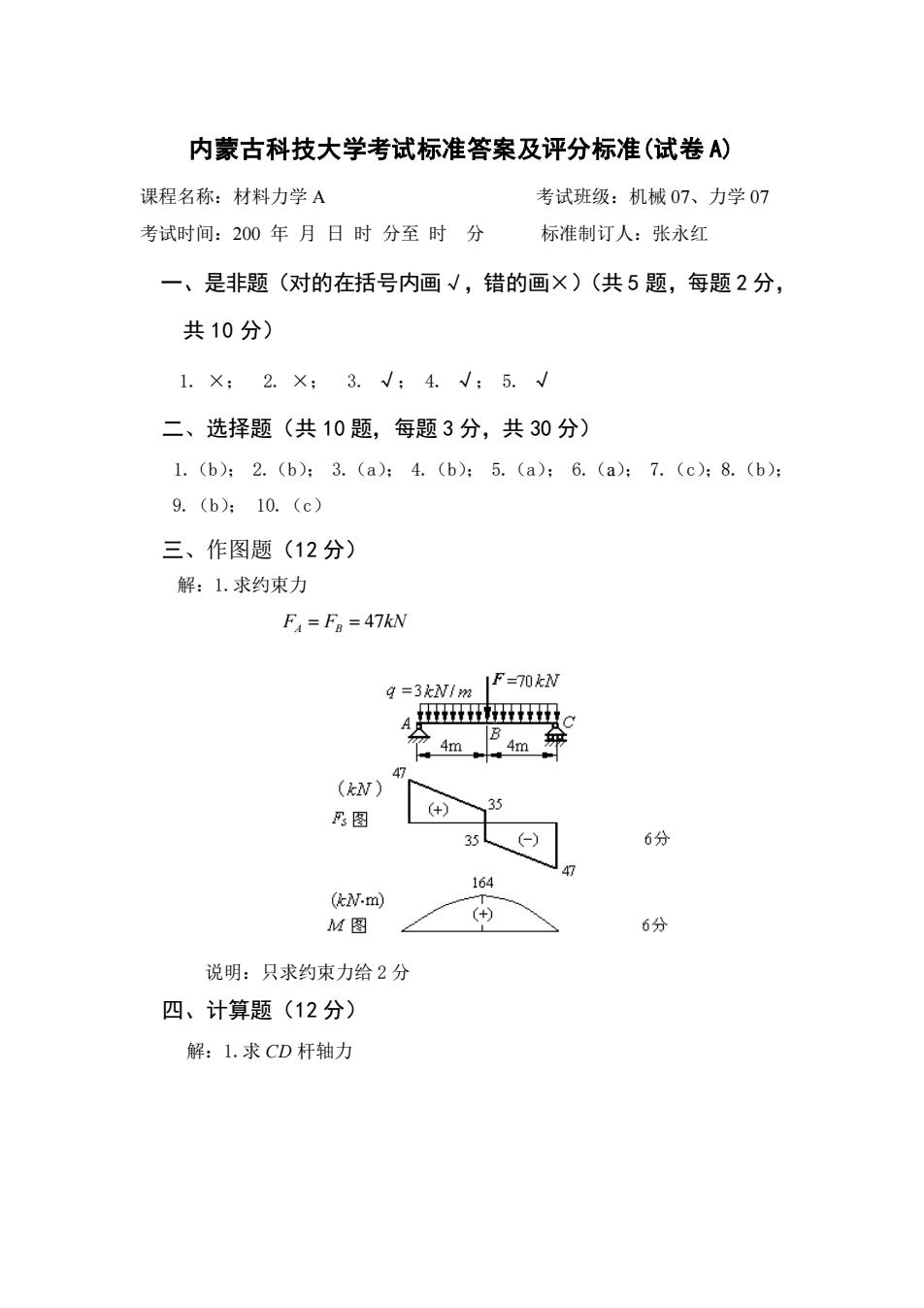
内蒙古科技大学考试标准答案及评分标准(试卷 A) 课程名称:材料力学 A 考试班级:机械 07、力学 07 考试时间:200 年 月 日 时 分至 时 分 标准制订人:张永红 一、是非题(对的在括号内画√,错的画×)(共 5 题,每题 2 分, 共 10 分) 1. ×; 2. ×; 3. √; 4. √; 5. √ 二、选择题(共 10 题,每题 3 分,共 30 分) 1.(b); 2.(b); 3.(a); 4.(b); 5.(a); 6.(a); 7.(c);8.(b); 9.(b); 10.(c) 三、作图题(12 分) 解:1.求约束力 FA = FB = 47kN 说明:只求约束力给 2 分 四、计算题(12 分) 解:1.求 CD 杆轴力

∑M4=0Fo2l-F.31=0 F 4分 2.校核CD杆强度 产×20 -=119.4MPa o∠] CD杆安全 4分 3.求许可载荷 a-学 Fs回_×202x160=3.5kN 6 6 故许可载荷F=33.5kW 4分 五、计算题(12分) 解:(1)画弯矩图 F 13.6kW.m M4=-F.2a=-20×0.68=-13.6kWm 危险截面为A截面 5分 (2)设计截面尺寸 由m奇-1B62s7x0am 60
M A = 0 FCD 2l − F 3l = 0 FCD F 2 3 = 4 分 2.校核 CD 杆强度 MPa d F A FCD 119.4 20 6 6 25 10 2 3 2 = = = = CD 杆安全 4 分 3.求许可载荷 = A FCD kN d F 33.5 6 20 160 6 2 2 = = 故许可载荷 F = 33.5kN 4 分 五、计算题(12 分) 解: (1)画弯矩图 MA = −F 2a = −200.68 = −13.6kNm 危险截面为 A 截面 5 分 (2)设计截面尺寸 由 3 3 6 226.7 10 60 13.6 10 mm M W A =

6=267x10m 5分 因h=3b 所以38=2267x10 b=151.13×103=53.3mm 取b=54mm h=3b=162mm 2分 六、计算题(12分) 解g± =90±V302+40 =90±50MPa 5分 =140MPa:=40MPa: 03=0 2分 7m-i,a-10=70Pa 2分 6=a,-lo,+a,月=0.65x103 62=a,-h46,+a,】=0025x10 6=66-6+o,月=-0.225x10 3分 七、计算题(12分) 解:法1:叠加法 F单独作用时 3E1 2E7 5分 g单独作用时
3 3 2 226.7 10 6 mm bh W = = 5 分 因 h = 3b 所以 3 3 226.7 10 2 3 b = b 151.13 10 53.3mm 3 3 = = 取 b = 54mm h = 3b =162mm 2 分 六、计算题(12 分) 解: min max 2 2 2 2 xy x y x y + − + = 2 2 = 90 30 + 40 =90 50MPa 5 分 1 =140MPa ; 2 = 40MPa ; 3 = 0 2 分 70MPa 2 140 2 1 3 max = = − = 2 分 ( ) 3 1 1 2 3 0.65 10 1 − = − + = E ( ) 3 2 2 1 3 0.025 10 1 − = − + = E ( ) 3 3 3 1 2 0.225 10 1 − = − + = − E 3 分 七、计算题(12 分) 解:法 1:叠加法 F 单独作用时 ( ) EI qa EI F a B 3 8 3 2 3 4 1 = − = − ( ) EI qa EI F a B 2 3 1 2 2 2 = − = − 5 分 q 单独作用时 EI qa B C 8 4 2 = = −
08器 a=0a0器 5分 放a=an+8a+aa 8=0.+0a=-8 2分 法2:应用莫尔定理求解 五 A C CB段:Mk)=-Fx1 M(x)=-x M(x2)=-x 2 a,-k+r产Mt,a EI EI 器器需 6分 CB段:M)=-xM)=-1 Mx)=-1 a,=+ra EI EI
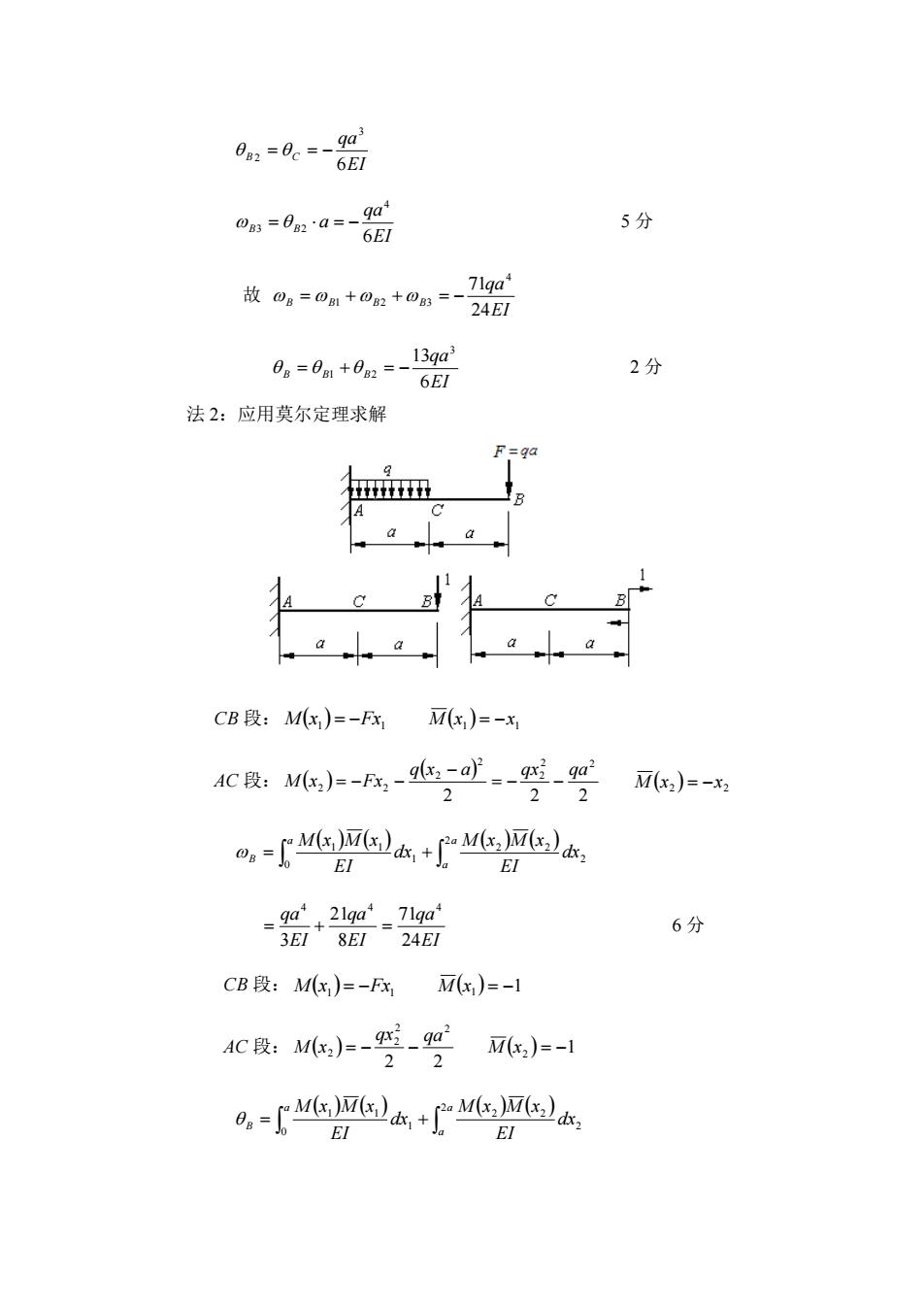
EI qa B C 6 3 2 = = − EI qa B B a 6 4 3 = 2 = − 5 分 故 EI qa B B B B 24 71 4 = 1 + 2 + 3 = − EI qa B B B 6 13 3 = 1 + 2 = − 2 分 法 2:应用莫尔定理求解 CB 段: ( ) 1 Fx1 M x = − ( ) 1 1 M x = −x AC 段: ( ) ( ) 2 2 2 2 2 2 2 2 2 2 q x a qx qa M x Fx = − − − = − − ( ) 2 2 M x = −x ( ) ( ) ( ) ( ) = + a a a B dx EI M x M x dx EI M x M x 2 2 2 2 0 1 1 1 EI qa EI qa EI qa 24 71 8 21 3 4 4 4 = + = 6 分 CB 段: ( ) 1 Fx1 M x = − M (x1 ) = −1 AC 段: ( ) 2 2 2 2 2 2 qx qa M x = − − M (x2 ) = −1 ( ) ( ) ( ) ( ) = + a a a B dx EI M x M x dx EI M x M x 2 2 2 2 0 1 1 1

器器器 6分 说明:列出部分弯矩方程可酌情给分,但部分最多不得超过4分
EI qa EI qa EI qa 6 13 6 10 2 3 3 3 = + = 6 分 说明:列出部分弯矩方程可酌情给分,但部分最多不得超过 4 分